2.5 塑性力学—应变状态
个人专栏—塑性力学
1.1 塑性力学基本概念 塑性力学基本概念
1.2 弹塑性材料的三杆桁架分析 弹塑性材料的三杆桁架分析
1.3 加载路径对桁架的影响 加载路径对桁架的影响
2.1 塑性力学——应力分析基本概念 应力分析基本概念
2.2 塑性力学——主应力、主方向、不变量 主应力、主方向、不变量
目录
- 个人专栏—塑性力学
-
目录
- 个人专栏—塑性力学
应变分析 \color{blue}应变分析 应变分析
- 应变与位移的关系
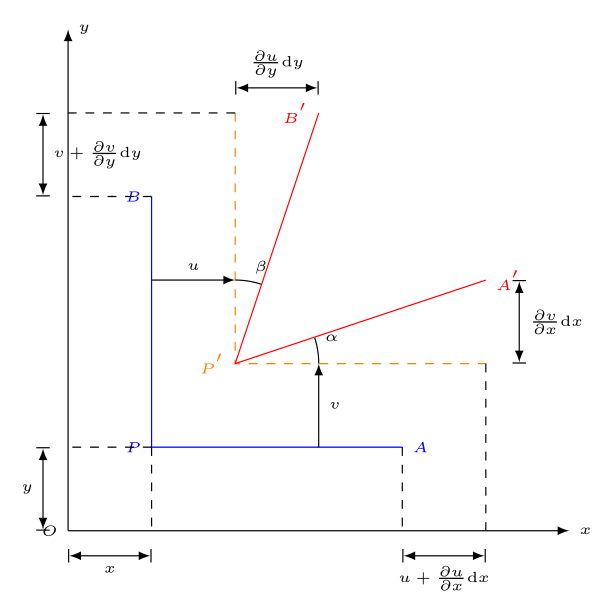
如图所示,由几何方程得:
{ ε x = ∂ u ∂ x γ x y = ∂ v ∂ x + ∂ u ∂ y ε y = ∂ v ∂ y γ y z = ∂ w ∂ y + ∂ v ∂ z ε z = ∂ w ∂ z γ z x = ∂ u ∂ z + ∂ w ∂ x \begin{cases} \varepsilon_x=\frac{\partial u}{\partial x} & \gamma_{xy}=\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\\ \varepsilon_y=\frac{\partial v}{\partial y} & \gamma_{yz}=\frac{\partial w}{\partial y}+\frac{\partial v}{\partial z}\\ \varepsilon_z=\frac{\partial w}{\partial z} & \gamma_{zx}=\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x} \end{cases} ⎩ ⎨ ⎧εx=∂x∂uεy=∂y∂vεz=∂z∂wγxy=∂x∂v+∂y∂uγyz=∂y∂w+∂z∂vγzx=∂z∂u+∂x∂w
剪应变张量表示为:
{ ε x y = 1 2 γ x y = 1 2 ∂ v ∂ x + ∂ u ∂ y ε y z = 1 2 γ y z = 1 2 ∂ w ∂ y + ∂ v ∂ z ε z x = 1 2 γ z x = 1 2 ∂ u ∂ z + ∂ w ∂ x \begin{cases} \varepsilon_{xy}=\frac{1}{2}\gamma_{xy}=\frac{1}{2}{\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}}\\ \varepsilon_{yz}=\frac{1}{2}\gamma_{yz}=\frac{1}{2}{\frac{\partial w}{\partial y}+\frac{\partial v}{\partial z}}\\ \varepsilon_{zx}=\frac{1}{2}\gamma_{zx}=\frac{1}{2}{\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}} \end{cases} ⎩ ⎨ ⎧εxy=21γxy=21∂x∂v+∂y∂uεyz=21γyz=21∂y∂w+∂z∂vεzx=21γzx=21∂z∂u+∂x∂w
-
一点的应变状态:知道一点的6个独立的应变分量: ε x , ε y , ε z , γ x y , γ y z , γ z x \varepsilon_x,\varepsilon_y,\varepsilon_z,\gamma_{xy},\gamma_{yz},\gamma_{zx} εx,εy,εz,γxy,γyz,γzx,任一方向的应变即可确定,称该点的应变情况为应变状态。
-
应变分量 $\varepsilon_x,\varepsilon_y,\varepsilon_z,\varepsilon_{xy},\varepsilon_{yz},\varepsilon_{zx} $构成应变张量
ε i j = [ ε x ε x y ε x z ε y x ε y ε y z ε z x ε z y ε z ] = [ ε x 1 2 γ x y 1 2 γ x z 1 2 γ y x ε y 1 2 γ y z 1 2 γ z x 1 2 γ z y ε z ] ε i j = 1 2 ( u i , j + u j , i ) \begin{gather*} \varepsilon_{ij}=\begin{bmatrix} \varepsilon_x & \varepsilon_{xy} & \varepsilon_{xz} \\ \varepsilon_{yx} & \varepsilon_y & \varepsilon_{yz} \\ \varepsilon_{zx} & \varepsilon_{zy} & \varepsilon_z \end{bmatrix}=\begin{bmatrix} \varepsilon_x & \frac{1}{2}\gamma_{xy} & \frac{1}{2}\gamma_{xz} \\ \frac{1}{2}\gamma_{yx} & \varepsilon_y & \frac{1}{2}\gamma_{yz} \\ \frac{1}{2}\gamma_{zx} & \frac{1}{2}\gamma_{zy} & \varepsilon_z \end{bmatrix}\\ \varepsilon_{ij}=\frac{1}{2}(u_{i,j}+u_{j,i}) \end{gather*} εij= εxεyxεzxεxyεyεzyεxzεyzεz = εx21γyx21γzx21γxyεy21γzy21γxz21γyzεz εij=21(ui,j+uj,i)
- 应变张量的三个不变量
ε i j = [ ε 11 ε 12 ε 13 ε 21 ε 22 ε 23 ε 31 ε 32 ε 33 ] ε 3 − I 1 ε 2 + I 2 ε 2 − I 3 = 0 I 1 = ε x + ε y + ε z = ε 1 + ε 2 + ε 3 I 2 = ε x ε y + ε y ε z + ε z ε x − ε x y 2 − ε y z 2 − ε z x 2 = ε 1 ε 2 + ε 2 ε 3 + ε 3 ε 1 I 3 = ε x ε y ε z + 2 ε x y ε y z ε z x − ε x ε y z 2 − ε y ε z x 2 − ε z ε x y 2 = ε 1 ε 2 ε 3 \begin{gather*} \varepsilon_{ij}=\begin{bmatrix} \varepsilon_{11} & \varepsilon_{12} & \varepsilon_{13} \\ \varepsilon_{21} & \varepsilon_{22} & \varepsilon_{23} \\ \varepsilon_{31} & \varepsilon_{32} & \varepsilon_{33} \end{bmatrix}\\ \varepsilon^3-I_1\varepsilon^2+I_2\varepsilon^2-I_3=0\\ I_1=\varepsilon_x+\varepsilon_y+\varepsilon_z=\varepsilon_1+\varepsilon_2+\varepsilon_3\\ I_2=\varepsilon_x\varepsilon_y+\varepsilon_y\varepsilon_z+\varepsilon_z\varepsilon_x-\varepsilon_{xy}^2-\varepsilon_{yz}^2-\varepsilon_{zx}^2=\varepsilon_1\varepsilon_2+\varepsilon_2\varepsilon_3+\varepsilon_3\varepsilon_1\\ I_3=\varepsilon_x\varepsilon_y\varepsilon_z+2\varepsilon_{xy}\varepsilon_{yz}\varepsilon_{zx}-\varepsilon_x\varepsilon_{yz}^2-\varepsilon_y\varepsilon_{zx}^2-\varepsilon_z\varepsilon_{xy}^2=\varepsilon_1\varepsilon_2\varepsilon_3 \end{gather*} εij= ε11ε21ε31ε12ε22ε32ε13ε23ε33 ε3−I1ε2+I2ε2−I3=0I1=εx+εy+εz=ε1+ε2+ε3I2=εxεy+εyεz+εzεx−εxy2−εyz2−εzx2=ε1ε2+ε2ε3+ε3ε1I3=εxεyεz+2εxyεyzεzx−εxεyz2−εyεzx2−εzεxy2=ε1ε2ε3
- 应变偏张量的三个不变量
ε i j = [ ε m 0 0 0 ε m 0 0 0 ε m ] + [ ε 11 − ε m ε 12 ε 13 ε 21 ε 22 − ε m ε 23 ε 31 ε 32 ε 33 − ε m ] ⏟ e i j = ε m δ i j + e i j ε m = ε x + ε y + ε z 3 = ε 1 + ε 2 + ε 3 3 ε x − ε m = 2 ε x − ε y − ε z 3 , ε y − ε m = 2 ε y − ε x − ε z 3 , ε z − ε m = 2 ε z − ε y − ε x 3 \begin{gather*} \varepsilon_{ij}=\begin{bmatrix} \varepsilon_m & 0 & 0 \\ 0 & \varepsilon_m & 0 \\ 0 & 0 & \varepsilon_m \end{bmatrix}+\underbrace{\begin{bmatrix} \varepsilon_{11}-\varepsilon_m & \varepsilon_{12} & \varepsilon_{13} \\ \varepsilon_{21} & \varepsilon_{22}-\varepsilon_m & \varepsilon_{23} \\ \varepsilon_{31} & \varepsilon_{32} & \varepsilon_{33}-\varepsilon_m \end{bmatrix}}_{e_{ij}}=\varepsilon_m\delta_{ij}+e_{ij}\\ \varepsilon_m=\frac{\varepsilon_x+\varepsilon_y+\varepsilon_z}{3}=\frac{\varepsilon_1+\varepsilon_2+\varepsilon_3}{3}\\ \varepsilon_x-\varepsilon_m=\frac{2\varepsilon_x-\varepsilon_y-\varepsilon_z}{3}, \quad \varepsilon_y-\varepsilon_m=\frac{2\varepsilon_y-\varepsilon_x-\varepsilon_z}{3}, \quad \varepsilon_z-\varepsilon_m=\frac{2\varepsilon_z-\varepsilon_y-\varepsilon_x}{3} \end{gather*} εij= εm000εm000εm +eij ε11−εmε21ε31ε12ε22−εmε32ε13ε23ε33−εm =εmδij+eijεm=3εx+εy+εz=3ε1+ε2+ε3εx−εm=32εx−εy−εz,εy−εm=32εy−εx−εz,εz−εm=32εz−εy−εx
体积应变 $\theta=\varepsilon_x+\varepsilon_y+\varepsilon_z=3\varepsilon_m $,只引起单元体的体积改变;剪切应变: $e_{ij} $只产生形状改变。
I 1 ′ = e 11 + e 22 + e 33 = 0 I 3 ′ = ∣ e i j ∣ = e 1 e 2 e 3 I 2 ′ = 1 2 e i j e j i = 1 6 [ ( e 11 − e 22 ) 2 + ( e 22 − e 33 ) 2 + ( e 33 − e 11 ) 2 ] + e 12 2 + e 23 2 + e 31 2 = 1 6 [ ( e x − e y ) 2 + ( e y − e z ) 2 + ( e z − e x ) 2 ] + 1 4 ( γ x y 2 + γ y z 2 + γ z x 2 ) = 1 6 [ ( ε 1 − ε 2 ) 2 + ( ε 2 − ε 3 ) 2 + ( ε 3 − ε 1 ) 2 ] \begin{align*} I_1^{'}&=e_{11}+e_{22}+e_{33}=0\quad I_3^{'}=|e_{ij}|=e_1e_2e_3\\ I_2^{'}&=\frac{1}{2}e_{ij}e_{ji}=\frac{1}{6}[(e_{11}-e_{22})^2+(e_{22}-e_{33})^2+(e_{33}-e_{11})^2]+e_{12}^2+e_{23}^2+e_{31}^2\\ &=\frac{1}{6}[(e_x-e_y)^2+(e_y-e_z)^2+(e_z-e_x)^2]+\frac{1}{4}(\gamma_{xy}^2+\gamma_{yz}^2+\gamma_{zx}^2)\\ &=\frac{1}{6}[(\varepsilon_1-\varepsilon_2)^2+(\varepsilon_2-\varepsilon_3)^2+(\varepsilon_3-\varepsilon_1)^2] \end{align*} I1′I2′=e11+e22+e33=0I3′=∣eij∣=e1e2e3=21eijeji=61[(e11−e22)2+(e22−e33)2+(e33−e11)2]+e122+e232+e312=61[(ex−ey)2+(ey−ez)2+(ez−ex)2]+41(γxy2+γyz2+γzx2)=61[(ε1−ε2)2+(ε2−ε3)2+(ε3−ε1)2]
-
八面体剪应变:与三个应变主轴方向具有相同倾角平面上的剪应变
{ ε 8 = 1 3 ( ε 1 + ε 2 + ε 3 ) γ 8 = 2 3 ( ε 1 − ε 2 ) 2 + ( ε 2 − ε 3 ) 2 + ( ε 3 − ε 1 ) 2 = 8 3 I 2 ′ \begin{cases} \varepsilon_8=\frac{1}{3}(\varepsilon_1+\varepsilon_2+\varepsilon_3)\\ \gamma_8=\frac{2}{3}\sqrt{(\varepsilon_1-\varepsilon_2)^2+(\varepsilon_2-\varepsilon_3)^2+(\varepsilon_3-\varepsilon_1)^2}=\sqrt{\frac{8}{3}I_2^{'}} \end{cases} {ε8=31(ε1+ε2+ε3)γ8=32(ε1−ε2)2+(ε2−ε3)2+(ε3−ε1)2=38I2′ -
Lode应变参数
μ ε = 2 ε 2 − ε 1 − ε 3 ε 1 − ε 3 = 2 ε 2 − ε 3 ε 1 − ε 3 − 1 \mu_{\varepsilon}=\frac{2\varepsilon_2-\varepsilon_1-\varepsilon_3}{\varepsilon_1-\varepsilon_3}=2\frac{\varepsilon_2-\varepsilon_3}{\varepsilon_1-\varepsilon_3}-1 με=ε1−ε32ε2−ε1−ε3=2ε1−ε3ε2−ε3−1
-
单向拉伸 ε 1 = ε , ε 2 = ε 3 = − 0.5 ε , μ ε = − 1 \varepsilon_1=\varepsilon,\quad \varepsilon_2=\varepsilon_3=-0.5\varepsilon,\quad \mu_{\varepsilon}=-1 ε1=ε,ε2=ε3=−0.5ε,με=−1
-
单向压缩 $\varepsilon_3=-\varepsilon,\quad \varepsilon_2=\varepsilon_1=0.5\varepsilon,\quad \mu_{\varepsilon}=1 $
-
纯剪切 $\varepsilon_1=0.5\gamma,\quad \varepsilon_2=0,\quad \varepsilon_3=-0.5\gamma,\quad \mu_{\varepsilon}=0 $
-
等效应变
ε ˉ = 4 3 I 2 ′ = 2 3 ( e 1 − e 2 ) 2 + ( e 2 − e 3 ) 2 + ( e 3 − e 1 ) 2 = 2 3 e 1 2 + e 2 2 + e 3 2 \begin{align*} \bar{\varepsilon}&=\sqrt{\frac{4}{3}I_2^{'}}\\ &=\frac{\sqrt{2}}{3}\sqrt{(e_1-e_2)^2+(e_2-e_3)^2+(e_3-e_1)^2}\\ &=\sqrt{\frac{2}{3}}\sqrt{e_1^2+e_2^2+e_3^2} \end{align*} εˉ=34I2′=32(e1−e2)2+(e2−e3)2+(e3−e1)2=32e12+e22+e32
应用示例 \color{blue}应用示例 应用示例
- 已知位移分量 $u=(2x+y)a,v=(2y+x)a,w=-az $,求:应变张量并分解应变强度。
ε x = ∂ u ∂ x = 2 a , ε y = ∂ v ∂ y = 2 a , ε z = ∂ w ∂ z = − a γ x y = ∂ u ∂ y + ∂ v ∂ x = 2 a , ε x y = 1 2 γ x y = a ε y z = 1 2 ( ∂ v ∂ z + ∂ w ∂ y ) , ε z x = 1 2 ( ∂ w ∂ x + ∂ u ∂ z ) ε m = ε x + ε y + ε z 3 = a ε i j = [ 2 a a 0 a 2 a 0 0 0 − a ] = [ a 0 0 0 a 0 0 0 a ] + [ a a 0 a a 0 0 0 − 2 a ] \begin{gather*} \varepsilon_x=\frac{\partial u}{\partial x}=2a, \quad \varepsilon_y=\frac{\partial v}{\partial y}=2a, \quad \varepsilon_z=\frac{\partial w}{\partial z}=-a\\ \gamma_{xy}=\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}=2a, \quad \varepsilon_{xy}=\frac{1}{2}\gamma_{xy}=a\\ \varepsilon_{yz}=\frac{1}{2}(\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y}), \quad \varepsilon_{zx}=\frac{1}{2}(\frac{\partial w}{\partial x}+\frac{\partial u}{\partial z})\\ \varepsilon_m=\frac{\varepsilon_x+\varepsilon_y+\varepsilon_z}{3}=a\\ \varepsilon_{ij}=\begin{bmatrix} 2a & a & 0\\ a & 2a & 0\\ 0 & 0 & -a \end{bmatrix}=\begin{bmatrix} a & 0 & 0\\ 0 & a & 0\\ 0 & 0 & a \end{bmatrix}+\begin{bmatrix} a & a & 0\\ a & a & 0\\ 0 & 0 & -2a \end{bmatrix} \end{gather*} εx=∂x∂u=2a,εy=∂y∂v=2a,εz=∂z∂w=−aγxy=∂y∂u+∂x∂v=2a,εxy=21γxy=aεyz=21(∂z∂v+∂y∂w),εzx=21(∂x∂w+∂z∂u)εm=3εx+εy+εz=aεij= 2aa0a2a000−a = a000a000a + aa0aa000−2a
相关文章:

2.5 塑性力学—应变状态
个人专栏—塑性力学 1.1 塑性力学基本概念 塑性力学基本概念 1.2 弹塑性材料的三杆桁架分析 弹塑性材料的三杆桁架分析 1.3 加载路径对桁架的影响 加载路径对桁架的影响 2.1 塑性力学——应力分析基本概念 应力分析基本概念 2.2 塑性力学——主应力、主方向、不变量 主应力、主…...

1.机器人抓取与操作介绍-深蓝学院
介绍 操作任务 操作 • Insertion • Pushing and sliding • 其它操作任务 抓取 • 两指(平行夹爪)抓取 • 灵巧手抓取 7轴 Franka 对应人的手臂 6轴 UR构型去掉一个自由度 课程大纲 Robotic Manipulation 操作 • Robotic manipulation refers…...

六,Linux基础环境搭建(CentOS7)- 安装HBase
Linux基础环境搭建(CentOS7)- 安装HBase 大家注意以下的环境搭建版本号,如果版本不匹配有可能出现问题! 一、HBase下载及安装 HBase是一个分布式的、面向列的开源数据库,该技术来源于 Fay Chang 所撰写的Google论文“…...
《计算机网络网络层:连接虚拟世界的关键桥梁》
一、网络层概述 网络层在计算机网络中占据着至关重要的地位,它作为连接不同网络的关键层次,起着承上启下的作用。网络层的主要任务是实现网络互连,将数据设法从源端经过若干个中间节点传送到目的端,为分组交换网上的不同主机提供通…...

【AIGC】2024-arXiv-CtrLoRA:一种可扩展且高效的可控图像生成框架
2024-arXiv-CtrLoRA: An Extensible and Efficient Framework for Controllable Image Generation CtrLoRA:一种可扩展且高效的可控图像生成框架摘要1. 引言相关工作3. 方法3.1 准备工作3.3 有效适应新条件3.4 条件嵌入网络的设计 4. 实验4.1 实验设置4.2 与现有方法…...

立仪光谱共焦在玻璃上奥秘与应用
在现代工业和科学研究中,玻璃因其透明、坚硬和易加工的特性被广泛应用于各个领域。然而,玻璃的厚度测量一直是困扰业界的一大难题。传统的千分尺或电容式传感器虽然在一定程度上能满足生产需求,但在精度、效率以及适用范围上存在明显的局限。…...
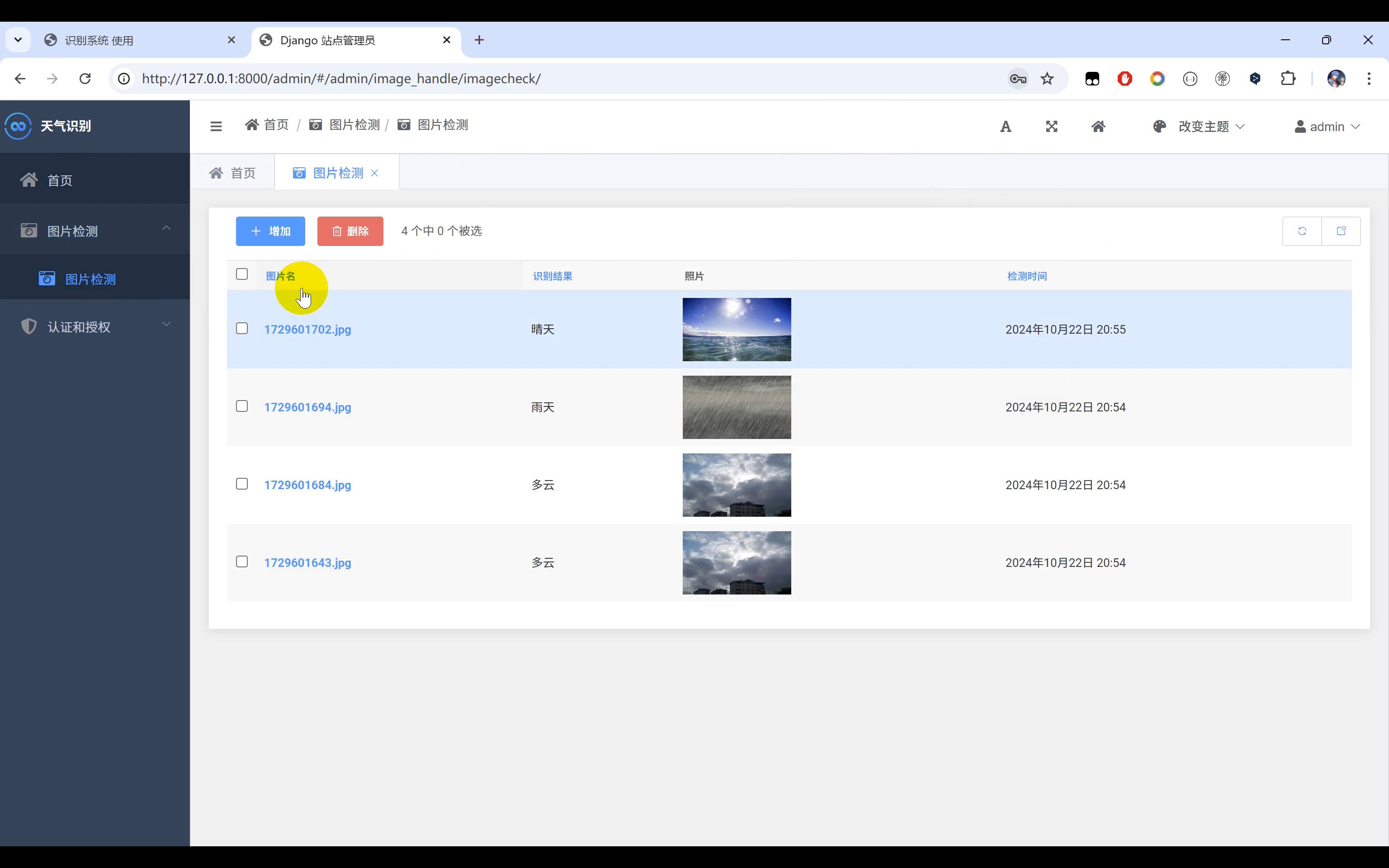
【天气识别系统】Python+卷积神经网络算法+人工智能+深度学习+TensorFlow+算法模型训练+Django网页界面
一、介绍 天气识别系统,以Python作为主要编程语言,通过收集了4种常见的天气图像数据集(多云、雨天、晴天、日出),然后基于TensorFlow搭建卷积神经网络算法模型,通过多轮迭代训练,最后得到一个识…...

MiniCTX:面向大语言模型定理证明的上下文相关基准测试系统
卡内基梅隆大学的研究人员推出MiniCTX,这是一个强大的基准测试系统,旨在通过整合前所未有的多重上下文元素(包括前提、先前证明、注释、符号以及导入和声明等结构组件)来彻底改变大型语言模型中定理证明能力的评估方式,…...

树莓派开发相关知识三PWM控制转速
基于树莓派PWM控制 控制L298N马达驱动转速 马达驱动转速 1、L298N电路图: 2、需要留意的有几点 INA~IND四个引脚分别控制OUTA-OUTD,即,INA高电平则OUTA有电。 ENA,ENB分别使能控制OUTA~OUTB以及OUTC~OUTD。 OUT口有VCC电压驱动…...

SpringBoot最常用的注解
1、RestController 作用:与Controller类似,但是RestController会自动将返回值转换为JSON格式。 2、RequestMapping 作用:用于映射请求URL和处理方法。 RequestMapping是Spring MVC框架中的一个核心注解,它用于映射HTTP请求和控…...

js 获取当前时间与前一个月时间
// 获取当前时间的毫秒数 var currentTimeMillis new Date().getTime();// 获取前一个月的Date对象 var dateLastMonth new Date(); dateLastMonth.setMonth(dateLastMonth.getMonth() - 1);// 获取前一个月的毫秒数 var timeMillisLastMonth dateLastMonth.getTime();conso…...
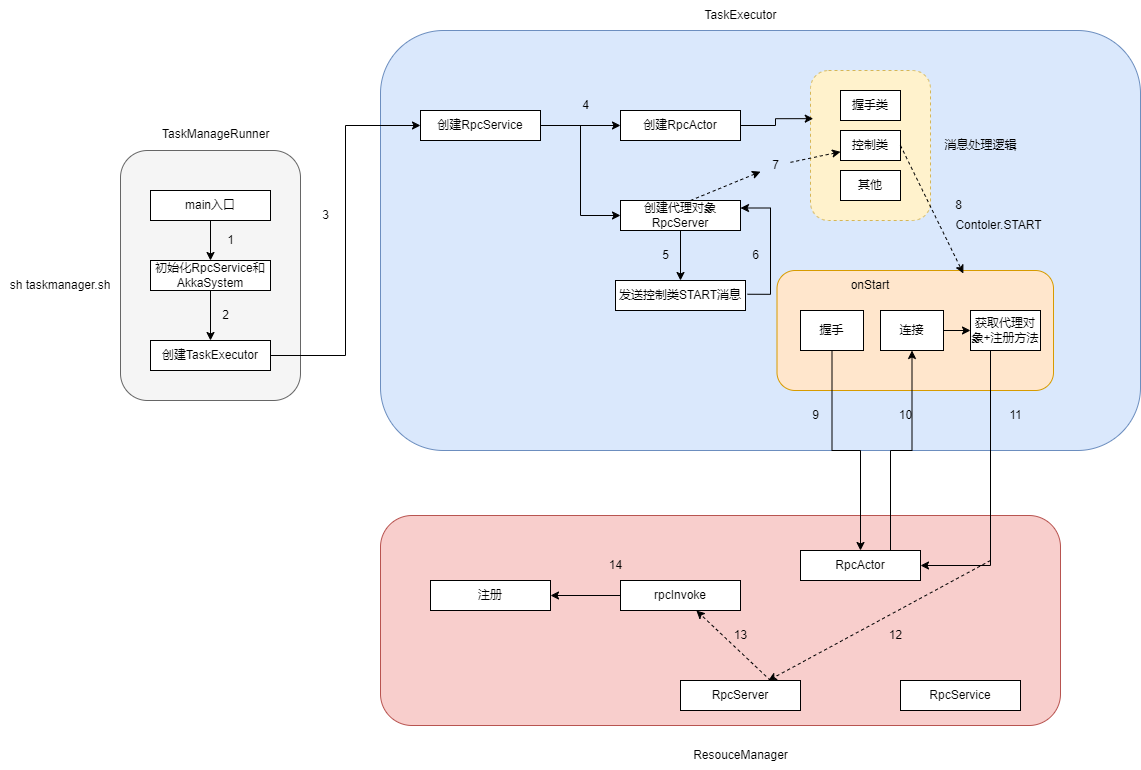
深度了解flink rpc机制(四) 组件启动流程源码分析
前言 目前已发布了3篇关于Flink RPC相关的文章,分别从底层通信系统akka/Pekko,RPC实现方式动态代理以及Flink RPC相关的组件做了介绍 深度了解flink rpc机制(一)-Akka/Pekko_flink pekko akka-CSDN博客 深度了解flink rpc机制&…...

C++基于opencv的视频质量检测--遮挡检测
文章目录 0.引言1. 原始代码分析1.1 存在的问题 2. 优化方案3. 优化后的代码4. 代码详细解读4.1. 输入检查4.2. 图像预处理4.3. 高斯模糊4.4. 梯度计算4.5. 计算梯度幅值和方向4.6. 边缘检测4.7. 计算边缘密度4.8. 估计遮挡程度4.9. 限定结果范围4.10. 返回结果 0.引言 视频质…...

手机玩潜水员戴夫?GameViewer远程如何随时随地玩潜水员戴夫教程
如果你是潜水员戴夫的忠实玩家,你知道如何在手机上玩潜水员戴夫吗?潜水员戴夫是一个以神秘蓝洞为背景的海洋冒险游戏。在这个游戏里你白天可以在美丽的大海里打鱼,晚上可以经营寿司店。现在这个游戏也能实现用手机随时随地畅玩了!…...

UE5 喷射背包
首选创建一个输入操作 然后在输入映射中添加,shift是向上飞,ctrl是向下飞 进入人物蓝图中编写逻辑,变量HaveJatpack默认true,Thrust为0 最后...

【Vue3】第三篇
Vue3学习第三篇 01. 组件组成02. 组件嵌套关系03. 组件注册方式04. 组件传递数据Props05. 组件传递多种数据类型06. 组件传递Props校验07. 组件事件08. 组件事件配合v-model使用09. 组件数据传递10. 透传Attributes 01. 组件组成 在vue当中,组件是最重要的知识&…...

c++二级指针
如果要通过函数改变一个指针的值,要往函数中传入指针的指针 如果要通过函数改变一个变量的值,那就要往函数中传入这个变量的地址 改变a的值和b的值 #include <iostream>using namespace std;void swap(int* a, int* b) {int temp *a;*a *b;*b …...

客户端存储 — IndexedDB 实现分页查询
前言 相信 IndexedDB 大家都有过了解,但是不一定每个人都有过实践,并且其中涉及到事务、游标等概念,会导致在初次使用时会有些不适应,那么本文会通过 IndexedDB 实现分页查询的形式进行实践,在开始之前,可…...

logback 如何将日志输出到文件
如何作 将日志输出到文件需要使用 RollingFileAppender,该 Appender 必须定义 rollingPolicy ,另外 rollingPollicy 下必须定义 fileNamePattern 和 encoder <appender name"fileAppender" class"ch.qos.logback.core.rolling.Rollin…...

Files.newBufferedReader和Files.readAllLines
在Java中,Files.newBufferedReader 和 Files.readAllLines 都是用于从文件中读取数据的工具方法,但它们的使用场景和功能有所不同。下面我将详细解释这两个方法的含义、用途、区别、优缺点以及各自的使用场景。 1. Files.newBufferedReader 含义和用途…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...
