Codeforces Round 981 (Div. 3) (A~F)
文章目录
- A. Sakurako and Kosuke
- 思路
- code
- B. Sakurako and Water
- 思路
- code
- C. Sakurako's Field Trip
- 思路
- code
- D. Kousuke's Assignment
- 思路
- code
- E. Sakurako, Kosuke, and the Permutation
- 思路
- code
- F. Kosuke's Sloth
- 思路
- code
Codeforces Round 981 (Div. 3)
A. Sakurako and Kosuke
思路
签到题,直接判断奇偶即可
code
void solve(){int n;cin >> n;if(n & 1) cout << "Kosuke" << endl;else cout << "Sakurako" << endl;return ;
}
B. Sakurako and Water
思路
考点:模拟
从头开始遍历,如果当前数 < 0,则说明这个数需要进行增加操作,那就遍历这个数的对角线,找出最大值,将这个对角线都加上最大值即可
将这些最大值全部累加,最后输出即可
code
const int N=1000;
int a[N][N];
void solve(){int n;cin >> n;for(int i=1;i<=n;++i)for(int j=1;j<=n;++j){cin >> a[i][j];}int ans=0;for(int i=1;i<=n;++i)for(int j=1;j<=n;++j){if(a[i][j]<0){int k=min(n-i+1,n-j+1);int s=0; for(int z=0;z<k;++z){if(a[i+z][j+z]<0) s=max(s,abs(a[i+z][j+z]));}for(int z=0;z<k;++z){a[i+z][j+z]+=s;}ans+=s;}}cout << ans << endl;return ;
}
C. Sakurako’s Field Trip
思路
考点:模拟
暴力解法,我们只需要考虑每一项 i i i 和它的镜像 n − i + 1 n-i+1 n−i+1 前后四项的值
如果这四个数有3个数的值相同,ans++,如果这四个数都相同,ans+=2
这时还需要考虑边界的问题,如果这个数为奇数并且遍历到中间这个数
那么我们就只需要考虑3个数,中间这个数和它前后这两个数
- 如果这三个数都相同,ans+=2
- 中间的数和前面的数相同或者中间的数和后面的数相同,ans++
如果这个数为偶数并且遍历到中间这两个数
那么我们只需要判断这两个数是否相同即可,相同ans++
讲起来有点复杂,实际上代码挺简单的
code
int a[N];
void solve(){int n;cin >> n;for(int i=1;i<=n;++i) cin >> a[i];int ans=0;for(int i=1,j=n;i<j;++i,--j){map<int,int> m;m.clear();if(i+1<j-1){m[a[i]]++,m[a[i+1]]++,m[a[j]]++,m[a[j-1]]++;for(auto x : m){if(x.se==3) ans++;if(x.se==4) ans+=2;}}else if(i+1==j-1){int x=a[i],y=a[i+1],z=a[j];if(x==y){if(x==z) ans+=2;else ans+=1;}else{if(y==z) ans+=1;}}else{if(a[i]==a[j]) ans+=1;}}cout << ans << endl;return ;
}
D. Kousuke’s Assignment
思路
考点:前缀和
对于数组 a a a ,先计算出它的前缀和,对于这个前缀和,我们维护当前 i i i 的上一个下标
如果遇见相同的前缀和,查询该前缀和的上一个下标是否小于上一段线段的结束位置
如果小于则选择,更新该前缀和的上一个下标为 i − 1 i-1 i−1
code
int a[N],sum[N];
void solve(){int n;cin >> n;for(int i=1;i<=n;++i){cin >> a[i]; sum[i]=sum[i-1]+a[i];} int ans=0,mx=-1;map<int,int> m;m[0]=0;for(int i=1;i<=n;++i){if(m.count(sum[i])){if(m[sum[i]]>mx){ans++;mx=i-1;}}m[sum[i]]=i;}cout << ans << endl;return ;
}
E. Sakurako, Kosuke, and the Permutation
思路
我们可以将这题看成一个环, i − > p i − > p p i − > ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ − > i i ->p_i->p_{pi}->······->i i−>pi−>ppi−>⋅⋅⋅⋅⋅⋅−>i 为一个循环节
我们需要将这个环拆分成若干个自环和环节数为2的环
如果这个环为自环,代表自己指向自己,如果这个环的环节为2,代表这个环里的两个数相互指向对面
把玩一下不难发现,替换 p p i = i p_{pi}=i ppi=i 优于 p i = i p_i=i pi=i 的操作
因为进行 p i = i p_i=i pi=i 的替换只能保证一个数是准确的,让这个数形成自环
而进行 p p i = i p_{pi}=i ppi=i 不仅可以保证一个数是准确的,还有可能会形成环节为2的环
因此我们只需要考虑 p p i = i p_{pi}=i ppi=i 的操作即可,用map存储环,每次进行替换操作维护map即可
code
int a[N];
void solve(){int n;cin >> n;map<int,int> m;for(int i=1;i<=n;++i){cin >> a[i];m[a[i]]=i;} int ans=0;for(int i=1;i<=n;++i){if(a[i]!=i && a[a[i]]!=i){int s=m[i];int t=a[i]; swap(a[s],a[t]);m[a[s]]=s;m[a[t]]=t;ans++;}}cout << ans << endl;return ;
}
F. Kosuke’s Sloth
思路
斐波那契数列在模 k k k 意义下有周期性(皮萨诺周期),且这个周期 < = 6 k <=6k <=6k
暴力枚举求出周期 r r r,则第 n n n 个数的下标为 r n rn rn
code
int f[N];
void solve(){int n,k;cin >> n >> k;f[1]=1,f[2]=1;if(k==1){cout << n%mod << endl;return ;}int ans=0;for(int i=3;i<=6e5+5;++i){f[i]=(f[i-1]+f[i-2])%k;if(f[i]%k==0){ans=i;break;}}cout << ((n%mod)*(ans%mod))%mod << endl;return ;
}
相关文章:
 (A~F))
Codeforces Round 981 (Div. 3) (A~F)
文章目录 A. Sakurako and Kosuke思路code B. Sakurako and Water思路code C. Sakurakos Field Trip思路code D. Kousukes Assignment思路code E. Sakurako, Kosuke, and the Permutation思路code F. Kosukes Sloth思路code Codeforces Round 981 (Div. 3) A. Sakurako and Ko…...
shell脚本实例(4)while实现1+...+100,linux新增用户
while实现1到100求和 #!/bin/bash/ s0 i1 #-le小于等于 while [ $i -le 100 ] dos$[ $s$i ]i$[ $i1 ] done echo $s echo $i 执行结果如下 修改用户名密码脚本 #!/bin/bash/ #提示用户输入用户名 read -p "请输入用户名:"username useradd $username #提…...

docker XML详解
下列为一个基本的运行docker镜像文件 {"Id": "62a82b0e69930e54c291095f632adde58dd0b247adba3a048385a55c87e38eba","Created": "2024-07-11T04:00:09.36091853Z","Path": "java","Args": ["-ja…...

web前端边框详解,弹性盒子的使用(仿写购物网页)
边框详解 1. 边框宽度(border - width) - 具体取值:可以是具体的长度值,如 px (像素)、 pt (点)、 em (相对单位)等。例如, border - width: 2px…...

【ACM出版,EI稳定检索,九大高校联合举办, IEEE Fellow支持】2024年计算机视觉与艺术研讨会(CVA 2024)
在线投稿:学术会议-学术交流征稿-学术会议在线-艾思科蓝 2024年计算机视觉与艺术国际学术会议(CVA 2024)作为2024年人工智能、数字媒体技术与交互设计国际学术会议(ICADI 2024)的分会。此次大会旨在汇聚全球在计算机视觉与艺术…...
认识软件测试
博主主页: 码农派大星. 数据结构专栏:Java数据结构 数据库专栏:MySQL数据库 JavaEE专栏:JavaEE 软件测试专栏:软件测试 关注博主带你了解更多知识 1. 什么是测试? 测试在⽣活中处处可⻅ 例子: 对某款购物软件进⾏测试 启动测试:点击软件图标&#…...
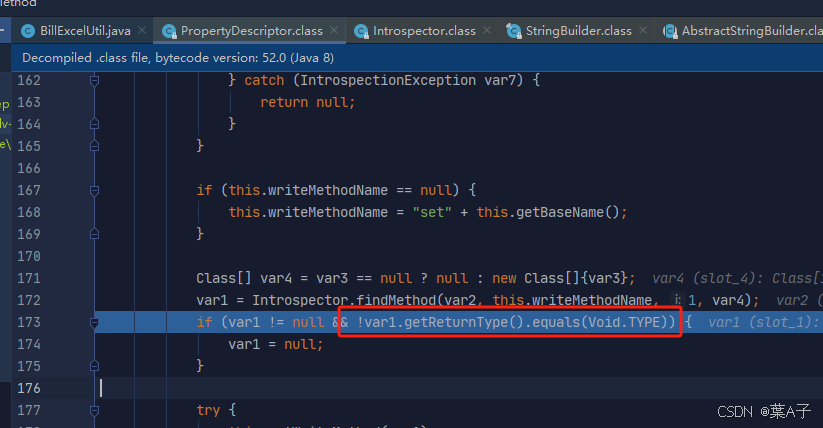
poi处理excel文档时,与lombok的@Accessors(chain = true)注解冲突
poi在反射封装数据时会判断set方法的返回是不是Void,加上Accessors会造成NoSuchMethodException异常...

我接触csdn中的c++的时间
大家好,我是AC使者,不知不觉我也来到CSDN半年了!在这半年我也看到了自身的不足,我也还有了很多粉丝,所以我今天来总结一下这半年的东西。 第一篇--------结构体数组 关于结构体数组的理解-CSDN博客 第二篇--------字…...
的使用)
go语言多态性(接口interface)的使用
前言 在Go语言中,接口类型(interface)完全可以作为一个函数的参数。这是Go语言多态性的一个重要体现,允许函数接受任何实现了接口中定义的方法的类型的实例。 一、接口(interface)定义 type Reader inte…...
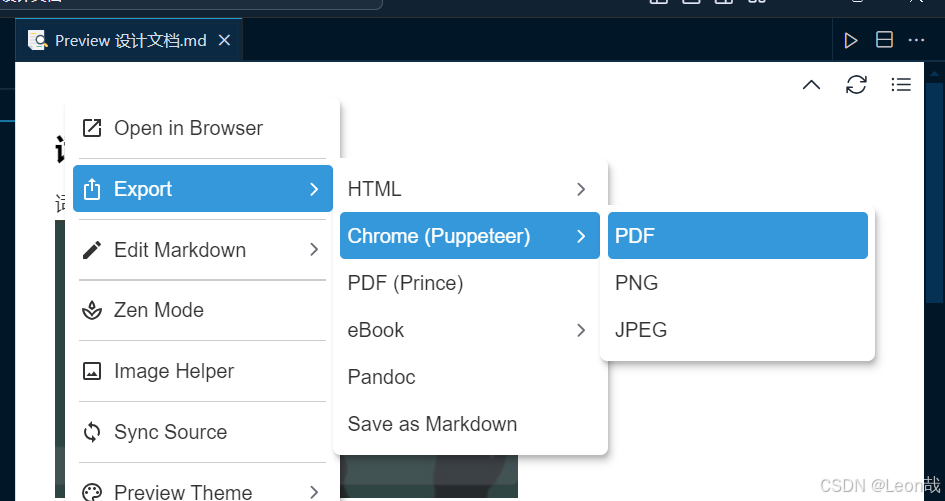
如何将markdown文件转换为pdf
最近笔者在用vscode写markdown,但是提交时往往需要交pdf。所以就涉及到如何将markdown转化为pdf格式。 首先,需要在vscode上安装插件 markdown Preview Enhanced 之后在vscode的右上角即可看到下述图标,点击,vscode右半面就会显示…...

【python实操】python小程序之测试报告
引言 python小程序之测试报告 文章目录 引言一、测试报告1.1 概念1.1.1 使用Pytest和Allure生成测试报告1.1.2 使用unittest和HTMLTestRunner生成测试报告1.1.3 总结 1.2 题目1.3 代码1.3 代码解释 二、思考 一、测试报告 1.1 概念 python生成测试报告,常用的方法包…...
【Java基础】2、Java基础语法
f2/fnf2:选中点中的文件名 1.注释 为什么要有注释? 给别人和以后的自己可以看懂的解释 注释含义 注释是在程序指定位置的说明性信息;简单理解,就是对代码的一种解释 注释分类 单行注释 //注释信息 多行注释…...
)
MATLAB基础应用精讲-【数模应用】本量利分析(Cost-Volume-Profit Analysis)
目录 前言 几个高频面试题目 本量利分析与量本利分析的区别 算法原理 发展历程 几个相关概念 什么是CVP分析 基本假设 注意事项 本量利分析的作用 基本原理 多种产品量本利分析 盈亏平衡分析 目标利润分析 敏感性分析 边际分析 本量利分析基本模型 应用场景 …...

实习冲刺Day7
算法题 合并两个有序链表 class Solution { public:void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {for (int i 0; i<n; i) {nums1[m i] nums2[i];//直接将num2的数据插入到num1的尾部}sort(nums1.begin(), nums1.end());//排…...

《Python游戏编程入门》注-第4章1
《Python游戏编程入门》的第4章是“用户输入:Bomb Cathcer游戏”,通过轮询键盘和鼠标设备状态实现Bomb Cathcer游戏。 1 Bomb Cathcer游戏介绍 “4.1 认识Bomb Cathcer游戏”内容介绍了Bomb Cathcer游戏的玩法,即通过鼠标来控制红色“挡板”…...

一些硬件知识【2024/10/29】
千兆以太网有8条信号线,百兆以太网有4条线: 网络变压器构造图: 百兆以太网拓扑: BOB Smith电路: 【以太网接口电 路设计】https://www.bilibili.com/video/BV1i3411u7bv?vd_source3cc3c07b09206097d0d8b0aefdf07958&a…...
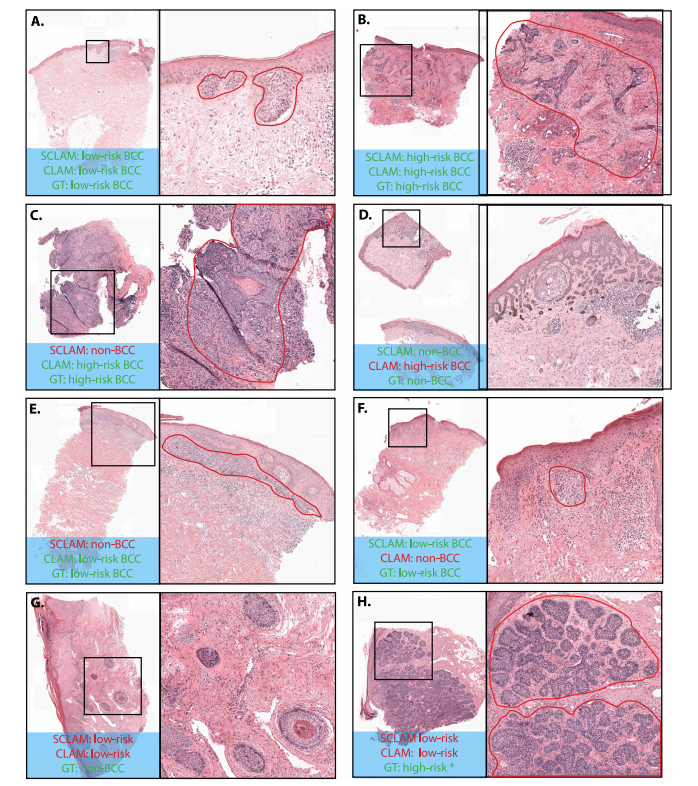
利用弱监督学习在全切片病理图像中检测和分型基底细胞癌|文献速递-基于生成模型的数据增强与疾病监测应用
Title 题目 Detection and subtyping of basal cell carcinoma in whole-slide histopathology using weakly-supervised learning 利用弱监督学习在全切片病理图像中检测和分型基底细胞癌 01 文献速递介绍 基底细胞癌 (BCC) 的发病率正在给病理诊断带来压力。BCC 的发病率…...

leetcode刷题笔记——15.三数之和
一、问题描述 给定一个整数数组 nums,判断是否存在三元组 [nums[i], nums[j], nums[k]],使得: i ! j、i ! k 且 j ! k nums[i] nums[j] nums[k] 0 需要返回所有和为 0 的三元组,且这些三元组不能重复。 输入输出 输入: 整…...

NLTK无法下载?
以下内容仅为当前认识,可能有不足之处,欢迎讨论! 文章目录 nltk无法下载怎么办?什么是NLTK?为什么要用NLTK?如何下载? nltk无法下载怎么办? 什么是NLTK? NLTK是学习自然…...
)
采用非递归快排实现找出数组中的前k个高频元素(python)
前k个高频元素 题目描述解题思路代码实现 题目描述 给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。 输入: nums [1,1,1,2,2,3], k 2 输出: [1,2] 解题思路 (1)先对给定的列表进行…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

leetcode73-矩阵置零
leetcode 73 思路 记录 0 元素的位置:遍历整个矩阵,找出所有值为 0 的元素,并将它们的坐标记录在数组zeroPosition中置零操作:遍历记录的所有 0 元素位置,将每个位置对应的行和列的所有元素置为 0 具体步骤 初始化…...

Canal环境搭建并实现和ES数据同步
作者:田超凡 日期:2025年6月7日 Canal安装,启动端口11111、8082: 安装canal-deployer服务端: https://github.com/alibaba/canal/releases/1.1.7/canal.deployer-1.1.7.tar.gz cd /opt/homebrew/etc mkdir canal…...

开源 vGPU 方案:HAMi,实现细粒度 GPU 切分
本文主要分享一个开源的 GPU 虚拟化方案:HAMi,包括如何安装、配置以及使用。 相比于上一篇分享的 TimeSlicing 方案,HAMi 除了 GPU 共享之外还可以实现 GPU core、memory 得限制,保证共享同一 GPU 的各个 Pod 都能拿到足够的资源。…...
