一篇文章入门傅里叶变换
文章目录
- 傅里叶变换
- 欧拉公式
- 傅里叶变换
- 绕圈记录法
- 质心记录法
- 傅里叶变换公式
- 第一步:旋转的表示
- 第二步:缠绕的表示
- 第三步:质心的表示
- 最终步:整理积分限和系数
- 参考文献
傅里叶变换
在学习傅里叶变换之前,我们先来了解一下欧拉公式。顺便说一下,『欧拉公式』在世界上最伟大的十个公式中排第二名,而『傅里叶变换』在世界上最伟大的十个公式中排第七名。
欧拉公式
在数学中,对于数的集合,在一维数轴上,加法操作可以视为沿着数轴的平移,而乘法操作则可以视为数轴上的伸缩变化。具体来说:
- 加法:在一维数轴上,给一个数加上另一个数,相当于将该数在数轴上向右(或向左,如果是负数)平移相应的距离
- 乘法:在一维数轴上,将一个数乘以另一个数,则相当于将该数在数轴上按比例伸缩
在二维平面上,如果我们想将一个点(比如 ( 1 , 0 ) (1,0) (1,0))移动到另一个点,可以先在横轴方向上平移,再在纵轴方向上平移即可实现。
除了平移外,也可以利用伸缩和旋转来达到同样的效果。伸缩操作即为点的倍乘,但旋转该如何表达呢?
- 仅使用旋转,就可以将 ( 1 , 0 ) (1,0) (1,0)变换到 ( − 1 , 0 ) (-1,0) (−1,0)
- 在复平面中,存在一个定义: − 1 = i × i -1=i\times i −1=i×i → \rightarrow →当单位 i i i表示旋转 90 ° 90° 90°时,进行两次相同的操作即可从 ( 1 , 0 ) (1,0) (1,0)变换到 ( − 1 , 0 ) (-1,0) (−1,0)
- 如果一次 i i i操作是逆时针旋转 90 ° 90° 90°,正好会落在二维平面y轴上的 ( 0 , 1 ) (0,1) (0,1),该点距离原点的长度为单位长度
- 如果 y y y轴自带虚数单位,如 i , 2 i , 3 i ⋯ i,2i,3i\cdots i,2i,3i⋯,即可通过伸缩和旋转表示二维平面上的所有点
请大家思考一个问题: i i i为什么可以表示旋转?
我们来看一下旋转的定义:旋转是沿着一个圆弧运动的过程
可以通过泰勒展开式得到一个完美的桥梁,用来说明 i i i可以表示旋转的原因
e x = 1 + x + 1 2 ! x 2 + 1 3 ! x 3 + ⋯ s i n ( x ) = x − 1 3 ! x 3 + 1 5 ! x 5 + ⋯ c o s ( x ) = 1 − 1 2 ! x 2 + 1 4 ! x 4 + ⋯ \begin{gathered} e^x=1+x+\frac1{2!}x^2+\frac1{3!}x^3+\cdots \\ sin(x)=x-\frac1{3!}x^3+\frac1{5!}x^5+\cdots \\ cos(x)=1-\frac1{2!}x^2+\frac1{4!}x^4+\cdots \end{gathered} ex=1+x+2!1x2+3!1x3+⋯sin(x)=x−3!1x3+5!1x5+⋯cos(x)=1−2!1x2+4!1x4+⋯ ⇒ \Rightarrow ⇒代入 x = i θ x=i\theta x=iθ得: e i θ = 1 + i θ + 1 2 ! ( i θ ) 2 + 1 3 ! ( i θ ) 3 + 1 4 ! ( i θ ) 4 + 1 5 ! ( i θ ) 5 + ⋯ = ( 1 − θ 2 2 ! + θ 4 4 ! + ⋯ ) + i ( θ − θ 3 3 ! + θ 5 5 ! + ⋯ ) = c o s ( θ ) + i s i n ( θ ) \begin{aligned} e^{i\theta}& =1+i\theta+\frac1{2!}(i\theta)^2+\frac1{3!}(i\theta)^3+\frac1{4!}(i\theta)^4+\frac1{5!}(i\theta)^5+\cdots \\ &=(1-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}+\cdots)+i(\theta-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}+\cdots) \\ &=cos(\theta)+isin(\theta) \end{aligned} eiθ=1+iθ+2!1(iθ)2+3!1(iθ)3+4!1(iθ)4+5!1(iθ)5+⋯=(1−2!θ2+4!θ4+⋯)+i(θ−3!θ3+5!θ5+⋯)=cos(θ)+isin(θ)

e i θ e^{i\theta} eiθ表示一个圆心在原点,半径为1的单位圆 ⇒ \Rightarrow ⇒ e i θ e^{i\theta} eiθ等价于一种旋转, θ \theta θ为旋转角的度数
傅里叶变换
傅里叶变换是一个分解声音的过程,其公式为: F ( f ) = ∫ − ∞ ∞ g ( t ) e − 2 π i f t d t F(f)=\int_{-\infty}^{\infty}g(t)e^{-2\pi ift}dt F(f)=∫−∞∞g(t)e−2πiftdt
乍一看这个公式,肯定是看不懂的,我们需要对其进行分解,然后逐步进行理解
既然傅里叶变换是一个分解声音的过程,我们来看一下什么是声音。
声音的气压是一个随时间以正弦函数形态不断震荡的图像
假设,一个标准音A的频率是440Hz,则其每秒钟振动440次;另外一个低音D的频率是240Hz,则其每秒钟振动240次。如果两个音同时发生,产生的气压随时间变化的曲线就是把所有时间点的振幅加起来
而傅里叶变换,就是从一段随时间变化的气压曲线中,找到组成该气压曲线的原始气压曲线
假设我们有一个每秒钟3拍子的声音信号,它的图像如下(Intensity为强度),我们只关注前面的4.5秒

绕圈记录法
绕圈记录法:同一事物的不同角度 → \rightarrow →下面的动图是最关键的一步,是【看到】傅立叶变换的核心部分

- 把黄色曲线缠绕到一个圆上,大小是原本信号的振幅
- 圆周围的图像由白色的箭头绘制而成,速度可变,上图中的白色箭头移动速度是每秒钟转过半圈
- 此时,有两个频率在起作用,一个是信号的频率:3次震荡/秒;另一个是图像缠绕中心圆的频率,为0.5圈/秒。第二个频率可以自由改变,相当于一个变量,下面的动图直观的展现了缠绕速度变化时的可视化表现

从最开始的 0.79圈/秒一直变化到1.55圈/秒,再到最后的恰好是3圈/秒,和原来的信号3次震荡/秒相同,此时会出现一个非常稳定的图像
其实,我们只是把一个水平的轴缠绕到一个单位圆上,并用另一个速度的记录标尺(白色箭头)来画图,从另一个角度(维度)来看我们的信号
质心记录法
质心记录法:新维度的特征提取
我们可以发现,在上面动图中,当白色箭头记录的速度在某些特定的值时,画出来的图形非常稳定、形态清晰
我们在上面提到了一个可以自由改变的转圈速度,我们可以将这个可变化的转圈速度作为傅里叶变换中的自变量
至于输出是什么,我们可以观察下面的动图。当图像很混沌(没有规律,混乱的)时候,图像基本关于原点对称;稳定时,其实是“头重脚轻”的。描述“头重脚轻”最好的方法是使用质心,下面的动图直观展现了质心特征对图像特征的描述能力(红色点为质心)

考虑到质心是一个二维坐标,为了简洁和直观,取质心的横坐标来表示质心的特征
现在,我们可以得到傅里叶变换的输入和输出:
- 输入(横坐标):白色箭头的绕圈速度
- 输出(纵坐标):质心位置的横坐标
按照上面的说明来记录绘出图像,记录每个缠绕频率(速度)对应的质心位置(在横坐标等于零点处有一个很大的值,只是因为原来的图像没有关于横轴对称,有一个偏移量)

我们可以看到,新图像的横坐标写的是频率(Frequency),即缠绕圆圈的速度
我们已经得到一个可以用来表示信号频率的工具,把它应用到两个声音的组合图像中看看效果:

傅里叶变换公式
我们已经通过这样一个缠绕机器完成了时域到频域的转换

如何使用数学语言表达这个转圈记录机制呢?
第一步:旋转的表示
上述所有动图中的旋转之所以能够表示,是基于复平面上的指数函数原理,结合泰勒展开公式来实现的

更进一步,指数函数中,以 e e e为底的函数有着特殊的性质,如下面动图所示, e 2 π i t e^{2\pi it} e2πit表示的是一秒钟一圈的旋转方程,可以通过频率 f f f控制旋转的速度,图中为 1 10 \frac{1}{10} 101

第二步:缠绕的表示
在傅立叶变换中,我们规定旋转是顺时针的,所以需要先加一个符号。假设原来的函数是 g ( t ) g(t) g(t),将两者的幅值相乘就能得到缠绕图像 g ( t ) e − 2 π i f t g(t)e^{-2\pi ift} g(t)e−2πift

第三步:质心的表示
那如何表示质心这一概念呢?有一种解决问题的途径是演绎推理,先从简单的特例出发,推广到一般,最后证明正确性即可
考虑如何求一个正方形的质心位置,我们只需在边框上取 n n n个等距离分布的点,并且算这几个点的位置的平均值。那么推广到一般情况,也使用类似的采样点的方式解决,如下面动图所示(紫红色的点即采样点),得到 1 N ∑ k = 1 N g ( t k ) e − 2 π i f t k \frac1N\sum_{k=1}^Ng(t_k)e^{-2\pi iftk} N1∑k=1Ng(tk)e−2πiftk

随着采样点的增加,需要使用积分来求解这个问题,如下面动图所示,得到 1 t 2 − t 1 ∫ t 1 t 2 g ( t ) e − 2 π i f t d t \frac1{t_2-t_1}\int_{t_1}^{t_2}g(t)e^{-2\pi ift}dt t2−t11∫t1t2g(t)e−2πiftdt

最终步:整理积分限和系数
看到常数项系数 1 t 2 − t 1 \frac1{t_2-t_1} t2−t11,如果忽略表达倍数关系的系数,对应的含义也会发生变化,不再是质心,而是信号存在的时间越久,位置是质心位置乘以一个倍数,它的值就越大。持续时长为3秒,那么新的位置就是原来质心位置的三倍;持续时长为6秒,就是原来的6倍
一般傅立叶变换公式的上下限是正负无穷,那它的几何直观是什么呢?

参考文献
1、傅里叶变换
2、泰勒公式
3、形象展示傅里叶变换
相关文章:

一篇文章入门傅里叶变换
文章目录 傅里叶变换欧拉公式傅里叶变换绕圈记录法质心记录法傅里叶变换公式第一步:旋转的表示第二步:缠绕的表示第三步:质心的表示最终步:整理积分限和系数 参考文献 傅里叶变换 在学习傅里叶变换之前,我们先来了解一…...

基于python的语音识别与蓝牙通信的温控系统
基于python的语音识别与蓝牙通信的温控系统毕设项目 大家好,我是陈辰学长,一名在 Java 圈辛勤劳作的码农。今日,要和大家分享的是一款基于python的语音识别与蓝牙通信的温控系统毕设项目。项目源码以及部署相关事宜,请联系陈辰学…...

Pandas Series学习
1.Series简介 Pandas Series类似表格的列(column),类似于一维数组,可以保存任何数据类型,具有标签(索引),使得数据在处理分析时更具灵活性。Series数据结构是非常有用的,…...

为什么要探索太空?这对我们有什么好处?
几个世纪以来,人类一直着迷于宇宙的奥秘,这驱使我们冒险离开地球,去探索太阳系之外的未知环境。在当今世界,我们为什么要进行太空探索之旅这个问题,远不止出于单纯的好奇。 归根结底,太空探索是一种必要之…...

uniapp开发【选择地址-省市区功能】,直接套用即可
一、效果展示 二、代码 <template><view><view class="user_info"><view class="item"...

3个模型的交互式多模型IMM,基于EKF的目标跟踪实例(附MATLAB代码)
文章目录 3个模型的IMM源代码运行结果代码介绍总结 3个模型的IMM 代码实现了基于 I M M IMM IMM(Interacting Multiple Model)算法的目标跟踪。它使用三种不同的运动模型(匀速直线运动、左转弯和右转弯)来预测目标的位置&#x…...

利用游戏引擎的优势
大家好,我是小蜗牛。 在当今快速发展的游戏产业中,选择合适的游戏引擎对开发者来说至关重要。Cocos Creator作为一款功能强大且灵活的游戏引擎,为开发者提供了丰富的工具和资源,使他们能够高效地开发出优秀的游戏。本文将探讨如何…...

一致角色的视频且唇形同步中文配音和免费音效添加
现在AI可以免费生成不带水印、不限时长的视频了,并且视频里的角色可以进行唇形同步配音。最重要的是,我还会分享给大家,怎么生成角色一致的动画场景,怎么使用场景图片生成完整的视频,并且我还会介绍一款,我…...

Spring学习笔记_14——@Qualifier
Qualifier 1. 解释 当Spring中存在多个类型相同但是名称不同的Bean时,使用Autowired注解向类的构造方法、方法、参数、字段中注入Bean对象时,首先会根据Bean的类型注入,如果存在多个类型相同的Bean时,会根据Bean的名称注入&…...

高级SQL技巧详解与实例
在数据处理与分析领域,高级SQL技巧是提升效率与准确性的关键。本文将结合参考资料,对高级SQL技巧进行系统的整理与解读,并通过实例展示其应用。 一、窗口函数 窗口函数是一种在SQL中执行复杂计算的强大工具,它们允许用户在一组行…...

实现PC端和安卓手机的局域网内文件共享
文章目录 一、准备工作1.1 笔记本(Win10)的设置(主要可分为3大部分:更改共享设置、创建本地用户、选择共享文件)1.2 台式机(Win7)的设置 二、实现共享文件夹的访问2.1 笔记本(Win10)访问台式机(Win7)2.2 台式机(Win7)访问笔记本(Win10)(一定要…...

腾讯云云开发深度解读:云数据库、云模板与AI生成引用的魅力
腾讯云云开发平台为开发者和潜在用户提供了丰富的解决方案,其中的云数据库、云模板和AI生成引用等产品尤为引人注目。这篇文件是我个人对这些产品的能力、应用场景、业务价值、技术原理的介绍和深度解读,最后也简单写一下新手如何进行相关产品的初步使用…...

预览 PDF 文档
引言 在现代Web应用中,文件预览功能是非常常见的需求之一。特别是在企业级应用中,用户经常需要查看各种类型的文件,如 PDF、Word、Excel 等。本文将详细介绍如何在Vue项目中实现 PDF 文档的预览功能。 实现原理 后端API 后端需要提供一个…...

Chromium 在WebContents中添加自定义数据c++
为了能在WebContents中添加自定义数据先看下几个关键类的介绍。 一、WebContents 介绍: WebContents是content模块核心,是呈现 Web 内容(通常为 HTML)位于矩形区域中。 最直观的是一个浏览器标签对应一个WebContents,…...
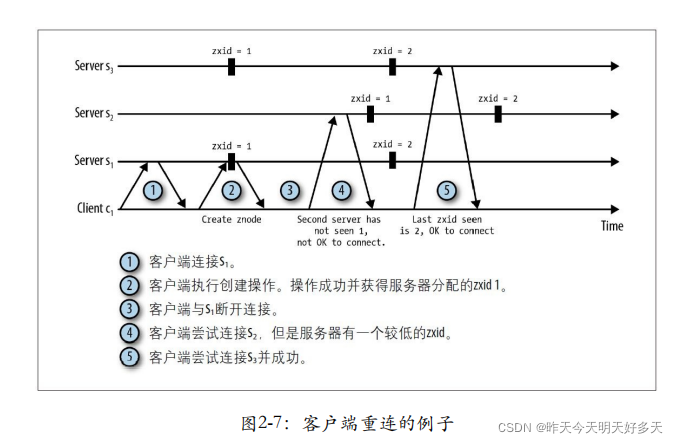
【Apache Zookeeper】
一、简介 1、场景 如何让⼀个应⽤中多个独⽴的程序协同⼯作是⼀件⾮常困难的事情。开发这样的应⽤,很容易让很多开发⼈员陷⼊如何使多个程序协同⼯作的逻辑中,最后导致没有时间更好地思考和实现他们⾃⼰的应⽤程序逻辑;又或者开发⼈员对协同…...

13.音乐管理系统(基于SpringBoot + Vue)
目录 1.系统的受众说明 2 需求分析 2.1用例图及用例分析 2.1.1 用户用例图及用例分析 2.1.2 管理员用例图及用例分析 2.2 系统结构图和流程图 2.2.1 音乐播放器的系统流程图(图2.2.1-1) 2.2.2 系统功能表(表2.2.2…...

如何从iconfont中获取字体图标并应用到微信小程序中去?
下面我们一一个微信小程序的登录界面的制作为例来说明,如何从iconfont中获取字体图标是如何应用到微信小程序中去的。首先我们看效果。 这里所有的图标,都是从iconfont中以字体的形式来加载的,也就是说,我们自始至终没有使用一张…...

C语言中的位操作
第一章 变量某位赋值与连续赋值 寄存器 | 值 //例如:a 1000 0011b a | (1<<2) //a 1000 0111 b 单独赋值 a | (3<<2*2) // 1011 0011b 连续赋值 第二章 变量某位清零与连续清零 寄存器 & ~() 值 //例子:a …...

Spring之HTTP客户端--RestTemplate的使用
原文网址:Spring之HTTP客户端--RestTemplate的使用_IT利刃出鞘的博客-CSDN博客 简介 本文介绍RestTemplate的用法。RestTemplate是Spring自带的HTTP客户端,推荐使用。 项目中经常需要使用http调用第三方的服务,常用的客户端如下࿱…...

vscode和pycharm在当前工作目录的不同|python获取当前文件目录和当前工作目录
问题背景 相信大家都遇到过一个问题:一个项目在vscode(或pycharm)明明可以正常运行,但当在pycharm(或vscode)中时,却经常会出现路径错误。起初,对于这个问题,我也是一知…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...
