深度学习:梯度下降算法简介
梯度下降算法简介
梯度下降算法
- 我们思考这样一个问题,现在需要用一条直线来回归拟合这三个点,直线的方程是 y = w ^ x + b y = \hat{w}x + b y=w^x+b,我们假设斜率 w ^ \hat{w} w^是已知的,现在想要找到一个最好的截距 b b b。

- 一条直线好与不好,我们可以用三个点到直线的长度来衡量,然后把这个距离误差写成一个最小二乘的方式,这个函数也被称为损失函数,我们的目标就是要找到一个 b b b,让损失函数最小就可以了,把直线的方程带进去然后化简一下,就可以看到这个损失函数L,其实是关于这个b的一个二次函数,其他系数也都可以直接计算出来。

- 我们假设这个二次函数是这样的,根据初中的知识,我们可以找到那个让损失函数最小的 b b b值,就在这个位置。

- 现在,我们换一种求解思路,我随便给定一个b的值,能不能通过迭代优化的方式找到最好的值呢,我们可以求出当前点的斜率,再乘一个常数 ϵ \epsilon ϵ,箭头的方向就是斜率的负方向,然后让b更新为b减去 ϵ \epsilon ϵ乘以斜率,这样就得到了一个新的值,这个新的值会比初始的损失函数更小,我们根据这个新的b值调整拟合函数的位置,然后继续迭代,当优化到最低点的时候,斜率等于 0 0 0, b b b不会再被更新,我们就找到了那个最好的值,优化过程结束,这就是梯度下降算法。

- 我们以一个更加一般的形式来表述这个算法,数据点不再是三个,而是很多点,函数是任意一个非线性函数,其中要优化的参数是 θ \theta θ,第i个样本点的损失函数可以写成这样的形式,我们首先可以求出L关于 θ \theta θ的偏导,也就是梯度值,然后做一个平均,为了更方便我们使用 g g g来代表这个长长的式子, θ \theta θ沿着梯度的负方向移动,就可以让损失函数更小了,其中的常数 ϵ \epsilon ϵ也被称为学习率,是人为设定的一个值,用来控制梯度下降的步长,最核心的步骤就是红框里面的两步了。

- 我们现在把这两个式子写在最上面,好好的看一看这个算法有没有什么问题,按照这个方法,我们首先需要计算出所有样本的损失函数梯度,然后求平均值来更新参数,如果我们的样本数量非常多,需要把全部的计算结果都保存下来,需要很大的内存开销,如果计算这么多的数据才更新一次参数,收敛速度也会比较慢,所以我们怎么改进这个问题呢,答案非常简单,就是每次只用少部分的数据更新就可以了。
随机梯度下降

随机梯度下降(SGD)的原理与实践应用
随机梯度下降(Stochastic Gradient Descent, SGD)是优化大规模数据集上的学习算法中非常关键的一种方法。它主要通过在每次迭代中随机选择一个样本子集(而非整个数据集)来计算梯度,从而更新模型参数。这种方法能够显著减少计算资源的需求,并加快迭代速度,是处理大数据环境下的优化问题的有效策略。
算法描述
在随机梯度下降中,假设我们有 n n n个样本,每次迭代选择 m m m个样本来进行参数更新,这些样本在每次迭代时被随机抽取,且每次抽取的样本集是不重复的。通过这种方式,SGD不仅减轻了内存的负担,也使得算法能够更快地遍历数据集。
数学表达式
对于函数 f ( x , θ ) f(x, \theta) f(x,θ),其中 θ \theta θ为模型参数, x i x_i xi和 y i y_i yi分别代表数据点及其标签,损失函数 L L L用于评估模型预测值与真实值之间的误差。梯度 g g g的计算公式如下:
g = 1 m ∇ θ ∑ i = 1 m L ( f ( x i , θ ) , y i ) g = \frac{1}{m} \nabla_\theta \sum_{i=1}^m L(f(x_i, \theta), y_i) g=m1∇θi=1∑mL(f(xi,θ),yi)
这里, g g g表示基于 m m m个随机抽取的样本计算得到的梯度平均值。模型参数的更新则遵循如下规则:
θ ← θ − ϵ g \theta \leftarrow \theta - \epsilon g θ←θ−ϵg
其中 ϵ \epsilon ϵ是学习率,控制着参数更新的步长。
理论与实践的联系
尽管使用随机样本可能会引入噪声,即梯度的估计可能不够精确或稳定,但在实践中,这种随机性反而帮助算法跳出局部最优解,朝向全局最优解进发。当样本方差较小,即数据点间的差异不大时,使用少量样本依然能够可靠地引导模型参数向着损失函数的全局最小值方向收敛。
总结
随机梯度下降通过每次迭代使用部分样本来更新模型参数,有效解决了传统梯度下降法在大规模数据集上应用时遇到的内存和速度瓶颈。这种方法不仅提高了计算效率,也在许多情况下,增强了模型在面对复杂数据分布时的泛化能力。因此,SGD成为了深度学习和机器学习领域中广泛使用的一种优化策略。
动量随机梯度下降

- 随机梯度下降并非所有情况都是有效的,深度学习网络训练往往是一个非凸的优化过程,在参数空间里面分布着各种山脊和山谷,我们来看这样一个山谷的例子,假设初始的网络参数处于这个位置,根据随机梯度下降,下一步它会沿着切面的方向移动,达到这个位置,以此类推,它的移动轨迹可能在山谷两侧来回震荡,难以收敛到一个更低的位置。
- 这个时候可能会想,如果它的运动能够假如一些阻尼,让它的移动更平滑一些,也许就会掉到山谷里,所以我们这样来处理,首先参数的初始化还是在这个位置,根据随机梯度下降更新到这个位置,在下一次更新的时候,我们不仅要计算新的梯度,还要保留上一次一部分的梯度,我们把这两个方向加在一起,构成新的更新方向,这样就可以得到一个更加合理的优化效果了,我们把保留的历史梯度称为动量,这个改进方向也被称为使用动量的随机梯度下降。
- 我们可以这样来理解,参数的移动收到来自梯度的一个力,但是它仍然要保留原始运动状态的一部分速度,所以运动起来路径才更加平滑,这也是动量的物理含义。

动量梯度下降法的数学表述与逻辑解析
动量梯度下降法(Momentum Gradient Descent)是一种在传统梯度下降算法基础上的改进算法,旨在加速学习过程,特别是在面对高曲率、小梯度或噪声较多的优化问题时更为有效。下面详细介绍这一算法的数学表述及其内在逻辑。
梯度计算
在每次迭代中,首先计算损失函数 L L L关于模型参数 θ \theta θ的梯度 g g g。这一步骤是基于随机选择的 m m m个样本来进行的,公式如下:
g = 1 m ∇ θ ∑ i = 1 m L ( f ( x i , θ ) , y i ) g = \frac{1}{m} \nabla_\theta \sum_{i=1}^m L(f(x_i, \theta), y_i) g=m1∇θi=1∑mL(f(xi,θ),yi)
此公式确保了即便在大规模数据集上,我们也能高效地估计全局梯度。
动量更新
动量项 v v v在算法中用以模拟物理中的惯性,即前一时刻的速度对当前速度的影响,从而帮助参数更新在正确的方向上持续前进,克服小梯度带来的停滞不前。动量的更新公式为:
v ← α v − ϵ g v \leftarrow \alpha v - \epsilon g v←αv−ϵg
其中, α \alpha α是动量因子,常见取值范围为[0.9, 0.99]。它决定了前一步动量对当前方向的影响程度,即历史梯度在多大程度上影响当前更新。 ϵ \epsilon ϵ是学习率,控制着梯度方向对参数更新的影响强度。
参数更新
参数 θ \theta θ的更新则是将动量直接加到当前参数上:
θ ← θ + v \theta \leftarrow \theta + v θ←θ+v
这一更新策略使得参数更新不仅考虑当前的梯度方向,还融入了过去梯度的方向和大小,有效避免了在陡峭的梯度或局部最小值处摇摆不定。
总结
动量梯度下降法通过引入动量项 v v v,使参数更新具有更好的连续性和平滑性,从而加速收敛并提高算法整体的效率和稳定性。这种方法特别适用于处理那些梯度变化复杂且容易陷入局部最小值的非凸优化问题。通过合理调控动量因子 α \alpha α和学习率 ϵ \epsilon ϵ,可以显著提升优化过程的性能。
学习率

- 我们再回到随机梯度下降的原始算法,其中还有一个非常重要的量我们没有讨论,那就是学习率。一般情况下,我们希望神经网络最开始快速的找到正确的收敛方向,会设置一个比较大的学习率,而随着训练过程,我们需要找到最好的结果,就不能盲目地追求速度了,而是让网络更加细致地优化,防止损失函数剧烈震荡,所以我们需要先设定一个初始值,然后每隔一段时间就降低学习率,但是这是一种非常粗犷的调整方式。
AdaGrad(2011)和RMSProp(2012)

AdaGrad和RMSProp算法的原理与实现
在深度学习的训练过程中,学习率的设定对模型的性能和收敛速度具有关键性影响。传统的固定学习率往往难以应对所有训练阶段的需求,因此自适应学习率算法应运而生。AdaGrad和RMSProp是两种流行的自适应学习率优化算法,它们通过调整学习率以适应参数的每个维度,从而优化学习过程。
AdaGrad算法
AdaGrad算法(Adaptive Gradient Algorithm)于2011年提出,其核心思想是累积过去所有梯度的平方和,以此调整每个参数的学习率。
算法步骤
-
梯度计算:
每次迭代中,首先计算损失函数 L L L关于参数 θ \theta θ的梯度 g g g:
g = 1 m ∇ θ ∑ i = 1 m L ( f ( x i , θ ) , y i ) g = \frac{1}{m} \nabla_\theta \sum_{i=1}^m L(f(x_i, \theta), y_i) g=m1∇θi=1∑mL(f(xi,θ),yi) -
累积平方梯度:
累积梯度的平方和 r r r随着时间不断增加:
r ← r + g 2 r \leftarrow r + g^2 r←r+g2 -
自适应学习率更新:
参数更新时,学习率通过梯度的平方累积量 r r r进行自适应调整,以平衡不同参数的学习速度:
θ ← θ − ϵ r + δ g \theta \leftarrow \theta - \frac{\epsilon}{\sqrt{r} + \delta} g θ←θ−r+δϵg
其中 δ \delta δ是一个很小的常数,防止分母为零。
AdaGrad的优势在于对频繁更新的参数采用较小的更新步长,而对不频繁更新的参数采用较大的更新步长。但其缺点也很明显,即随着训练的进行, r r r的累积可能会过大,导致学习率过早降低至接近于零,从而使得训练过程提前终止。
RMSProp算法
为了克服AdaGrad学习率快速衰减的问题,RMSProp算法在2012年被提出,通过引入衰减系数 ρ \rho ρ,对平方梯度进行指数加权平均,而不是简单的累加。
算法步骤
-
梯度计算:
同AdaGrad。 -
指数加权平方梯度:
r r r的更新公式采用指数加权移动平均,减少旧梯度的影响:
r ← ρ r + ( 1 − ρ ) g 2 r \leftarrow \rho r + (1 - \rho) g^2 r←ρr+(1−ρ)g2 -
参数更新:
类似于AdaGrad,但更新中的 r r r是平滑过的,避免了学习率过快衰减:
θ ← θ − ϵ r + δ g \theta \leftarrow \theta - \frac{\epsilon}{\sqrt{r} + \delta} g θ←θ−r+δϵg
RMSProp算法有效解决了AdaGrad中学习率持续衰减的问题,使学习率保持在一个更加合理的范围内,特别适合处理非平稳目标的训练。
总结
AdaGrad与RMSProp算法都通过调整学习率来优化训练过程,其中RMSProp通过改进累积梯度的方法,提供了一种更为稳健的方式来处理各种深度学习任务。这两种算法都是自适应学习率技术的重要发展,极大地促进了深度学习领域的进步。
Adam(2014)

Adam算法的综合描述
Adam算法(Adaptive Moment Estimation)是一种广泛使用的参数优化算法,它结合了动量(Momentum)方法和自适应学习率(Adaptive Learning Rate)技术,旨在提升梯度下降法在训练深度学习模型时的性能和稳定性。2014年提出的这一算法,通过细致地调节学习步长,可以更有效地训练复杂的非凸优化问题。
算法步骤详解
1. 计算梯度
首先,算法计算损失函数 L L L关于参数 θ \theta θ的梯度 g g g,该梯度是基于随机选择的 m m m个样本得出的:
g = 1 m ∇ θ ∑ i = 1 m L ( f ( x i , θ ) , y i ) g = \frac{1}{m} \nabla_\theta \sum_{i=1}^m L(f(x_i, \theta), y_i) g=m1∇θi=1∑mL(f(xi,θ),yi)
这一步是随机梯度下降的基础,用于确定参数更新的方向。
2. 更新动量累积变量 s s s
动量 s s s是梯度的指数加权平均,使用超参数 ρ 1 \rho_1 ρ1控制衰减率,可以视作加速度,帮助优化过程维持方向并增强稳定性:
s ← ρ 1 s + ( 1 − ρ 1 ) g s \leftarrow \rho_1 s + (1 - \rho_1) g s←ρ1s+(1−ρ1)g
3. 更新梯度平方的累积变量 r r r
变量 r r r是梯度平方的指数加权平均,使用超参数 ρ 2 \rho_2 ρ2控制,类似于RMSProp算法中的累积平方梯度,用于自适应调整学习率:
r ← ρ 2 r + ( 1 − ρ 2 ) g 2 r \leftarrow \rho_2 r + (1 - \rho_2) g^2 r←ρ2r+(1−ρ2)g2
4. 偏差修正
由于 s s s和 r r r在训练初期可能因初始化为0而偏低,Adam算法引入偏差修正来抵消这一影响,保证早期迭代时估计更准确:
s ^ = s 1 − ρ 1 t , r ^ = r 1 − ρ 2 t \hat{s} = \frac{s}{1 - \rho_1^t}, \quad \hat{r} = \frac{r}{1 - \rho_2^t} s^=1−ρ1ts,r^=1−ρ2tr
这里 t t t代表迭代次数。
5. 参数更新
最终,参数 θ \theta θ的更新公式如下,其中 ϵ \epsilon ϵ为学习率, δ \delta δ是为了维持数值稳定性而添加的小常数:
θ ← θ − ϵ s ^ r ^ + δ \theta \leftarrow \theta - \frac{\epsilon \hat{s}}{\sqrt{\hat{r}} + \delta} θ←θ−r^+δϵs^
这一步通过调整学习率,依赖于平滑处理过的梯度大小,有助于避免学习过程中的震荡和不稳定。
总结
Adam算法通过结合动量和自适应学习率的优点,提供了一种强大而灵活的方式来优化深度学习模型的参数。它不仅加速了收敛过程,而且通过自动调节学习率,增强了算法在面对不同梯度规模时的鲁棒性。Adam算法的这些特性使其在许多深度学习应用中成为首选的优化技术。
总结
深度学习中的梯度下降算法系列
在深度学习的训练过程中,梯度下降算法(Gradient Descent,简称GD)扮演着至关重要的角色。这一算法的核心机制是利用数据集的梯度信息来迭代更新模型参数,以最小化损失函数。接下来,我们将详细讨论其各种变体和进化。
1. 随机梯度下降(SGD)
由于全批量的梯度下降在面对大规模数据集时会受到内存限制和迭代速度的制约,学者们提出了随机梯度下降(Stochastic Gradient Descent,SGD)。这种方法每次迭代仅使用数据集中的一个小批量样本来计算梯度和更新参数。这不仅显著提高了计算效率,也有助于模型跳出局部最小值,提升全局搜索能力。
2. 动量法(Momentum)
为了加速SGD的收敛速度并提高其在复杂优化面(如非凸优化问题)中的表现,动量法被引入到算法中。动量法借鉴了物理中的动量概念,通过累积之前梯度的指数衰减平均来调整每次的参数更新,使得参数更新的方向不仅由当前的梯度决定,还由历史梯度的累积方向影响,从而有效减少振荡,加速收敛。
3. 自适应学习率算法
AdaGrad
为了应对学习率调整问题,AdaGrad算法被提出。它通过积累历史梯度的平方和来调整各参数的学习率,使得学习率逐渐减小,适用于处理稀疏数据。该算法特别适合应对大规模和稀疏的机器学习问题。
RMSProp
RMSProp算法对AdaGrad进行了改进,通过引入衰减系数来计算梯度的滑动平均的平方,解决了AdaGrad学习率持续下降过快的问题,使得算法在非凸设定下表现更佳。
4. Adam算法
结合了动量法和RMSProp的自适应学习率调整的优点,Adam(Adaptive Moment Estimation)算法成为了一种非常强大的优化算法,广泛应用于各种深度学习场景。Adam不仅考虑了梯度的一阶矩(即动量),还包括了梯度的二阶矩估计,其学习率的调整更为精细,能够自适应地调整不同参数的更新速度。
总结
从最初的梯度下降到SGD,再到动量法和各种自适应学习率技术,每一种改进都旨在解决优化过程中遇到的特定挑战,如加速收敛、逃离局部最小值或是处理非凸优化问题。Adam算法的提出,标志着这些技术的集大成,提供了一种高效、稳定且智能的方式来进行深度学习模型的训练。
相关文章:

深度学习:梯度下降算法简介
梯度下降算法简介 梯度下降算法 我们思考这样一个问题,现在需要用一条直线来回归拟合这三个点,直线的方程是 y w ^ x b y \hat{w}x b yw^xb,我们假设斜率 w ^ \hat{w} w^是已知的,现在想要找到一个最好的截距 b b b。 一条…...

SparkSQL整合Hive后,如何启动hiveserver2服务
当spark sql与hive整合后,我们就无法启动hiveserver2的服务了,每次都要先启动hive的元数据服务(nohup hive --service metastore)才能启动hive,之前的beeline命令也用不了,hiveserver2的无法启动,这也导致我…...

前端路由如何从0开始配置?vue-router 的使用
在 Web 开发中,路由是指根据 URL 的不同部分将请求分发到不同的处理函数或页面的过程。路由是单页应用(SPA, Single Page Application)和服务器端渲染(SSR, Server-Side Rendering)应用中的一个重要概念。 在开发中如何…...

Java中的运算符【与C语言的区别】
目录 1. 算术运算符 1.0 赋值运算符: 1.1 四则运算符: - * / % 【取余与C有点不同】 1.2 增量运算符: - * / % * 【右侧运算结果会自动转换类型】 1.3 自增、自减:、-- 2. 关系运算符 3. 逻辑运算符 3.1 短路求值 3.2 【…...
二、基础语法
入门了解 注释 **作用:**在代码中加一些注释和说明,方便自己或者其他程序员阅读代码 两种格式: 单行注释:// 描述信息 通常放在一行代码的上方,或者一条语句的末尾,对该行代码进行说明 多行注释&#x…...
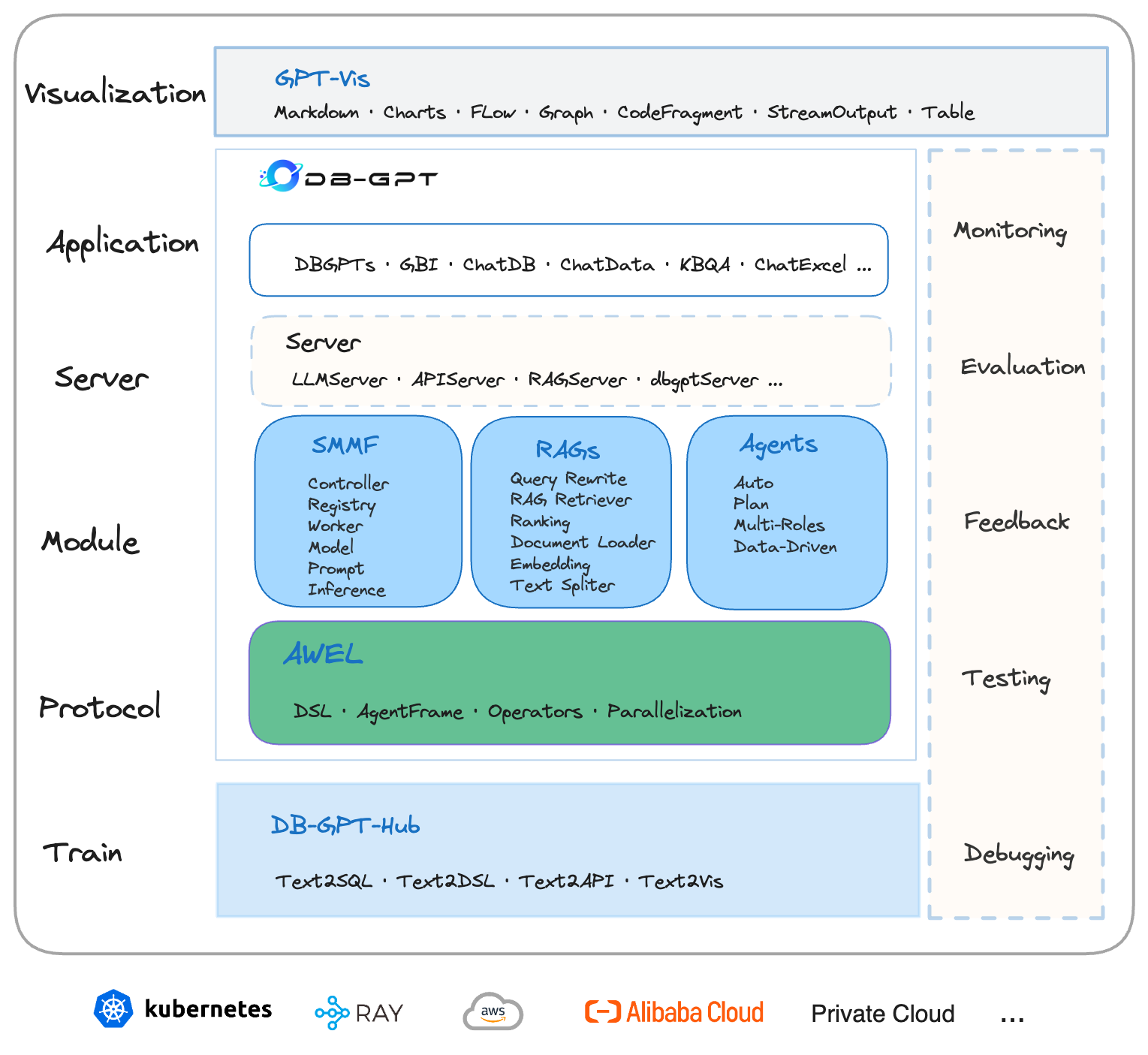
DB-GPT系列(一):DB-GPT能帮你做什么?
DB-GPT是一个开源的AI原生数据应用开发框架(AI Native Data App Development framework with AWEL and Agents),围绕大模型提供灵活、可拓展的AI原生数据应用管理与开发能力,可以帮助企业快速构建、部署智能AI数据应用,通过智能数据分析、洞察…...

【Python各个击破】numpy
简介 NumPy是一个开源的Python库,它提供了一个强大的N维数组对象和许多用于操作这些数组的函数。它是大多数Python科学计算的基础,包括Pandas、SciPy和scikit-learn等库都建立在NumPy之上。 安装 !pip install numpy导入 import numpy as np用法 # …...

【STM32 Blue Pill编程实例】-4位7段数码管使用
4位7段数码管使用 文章目录 4位7段数码管使用1、7段数码介绍2、硬件准备与接线3、模块配置4、代码实现在本文中,我们将介绍如何将 STM32 Blue Pill开发板与 4 位 7 段数码管连接,并在 STM32CubeIDE 中对其进行编程。 在文章中首先将介绍 4 位 7 段数码管及其与 STM32 Blue Pi…...
数据结构)
[进阶]java基础之集合(三)数据结构
文章目录 数据结构概述常见的数据结构数据结构(栈)数据结构(队列)数据结构(数组)数据结构(链表) 数据结构 概述 数据结构是计算机底层存储、组织数据的方式。是指数据相互之间是以什么方式排列在一起的。数据结构是为了更加方便的管理和使用数据,需要结合具体的业…...

《Apache Cordova/PhoneGap 使用技巧分享》
一、引言 在移动应用开发的领域中,Apache Cordova(也被称为 PhoneGap)是一个强大的工具,它允许开发者使用 HTML、CSS 和 JavaScript 等 Web 技术来构建跨平台的移动应用。这种方式不仅能够提高开发效率,还能降低开发成…...

SCP(Secure Copy
SCP(Secure Copy)是Linux系统下基于SSH协议的安全文件传输工具,用于在本地和远程主机间安全、快速地传输文件和目录。SCP命令通过加密传输确保数据的安全性,并且不占用过多系统资源。 SCP的基本用法 基本语法:…...

uniApp 省市区自定义数据
关于自定义省市区选择 其实也是用了 uniApp的内置组件 picker <picker mode"multiSelector" change"bindRegionChange" columnchange"bindMultiPickerColumnChange" :value"valueRegion" :range"multiArray"><v…...

图解Redis 06 | Hash数据类型的原理及应用场景
介绍 Hash 类型特别适合存储对象,例如用户信息等。 String类型也可以用于存储用户信息,Hash与String存储用户信息的区别如下图所示: 内部实现 Hash 类型 的底层数据结构是通过压缩列表(Ziplist)或哈希表ÿ…...

在 Windows 系统上设置 MySQL8.0以支持远程连接
在 Windows 系统上设置 MySQL8.0以支持远程连接的步骤如下: 步骤1: 修改 MySQL 配置文件1. 找到配置文件: MySQL 的配置文件通常为 my.ini,通常位于 C:\ProgramData\MySQL\MySQL Server8.0\(确保查看隐藏文件和文件夹)…...

四种基本的编程命名规范
目前,共有四种基本的编程命名规范,分别是匈牙利命名法、驼峰式命名法、帕斯卡命名法和下划线命名法,其中前三种命名法较为流行。 例如:iMyData是一个匈牙利命名法;myData是一个驼峰式命名法;MyData是一个帕…...

【前端】在 TypeScript 中使用 AbortController 取消异步请求
在 TypeScript 中使用 AbortController 来取消异步请求,尤其是像 fetch 这样的请求,可以提供一种优雅的方式来中止长时间运行的操作。下面是一个详细的步骤说明,展示如何在 TypeScript 中使用 AbortController 取消 fetch 请求。 步骤 1&…...

k8s知识点总结
docker 名称空间 分类 Docker中的名称空间用于提供进程隔离,确保容器之间的资源相互独立。主要分类包括: PID Namespace:进程ID隔离,使每个容器有自己的进程树,容器内的进程不会干扰其他容器或主机上的进程。 NET Nam…...

论文阅读:三星-TinyClick
《Single-Turn Agent for Empowering GUI Automation》 赋能GUI自动化的单轮代理 摘要 我们介绍了一个用于图形用户界面(GUI)交互任务的单轮代理,使用了视觉语言模型Florence-2-Base。该代理的主要任务是识别与用户指令相对应的UI元素的屏幕…...

Windows on ARM上使用sherpa-onnx实现语音识别
Windows on ARM上使用sherpa-onnx实现语音识别 下载模型准备声音文件测试下载模型 模型所在的地址在这里(),通过git命令将模型下载下来 模型:hfd地址 git clone https://hf-mirror.com/csukuangfj/sherpa-onnx-streaming-paraformer-bilingual-zh-en将如下的代码保存成一个…...

Unity 打包AB Timeline 引用丢失,错误问题
1、裁剪 在 link.xml 添加 <assembly fullname"Unity.Timeline" preserve"all"/> 上面这一步我其实做了,但还是不行,各种搜索,不得解,还有创建一个空的Timeline 放到 Resources目录下的,也…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...
OPENCV图形计算面积、弧长API讲解(1)
一.OPENCV图形面积、弧长计算的API介绍 之前我们已经把图形轮廓的检测、画框等功能讲解了一遍。那今天我们主要结合轮廓检测的API去计算图形的面积,这些面积可以是矩形、圆形等等。图形面积计算和弧长计算常用于车辆识别、桥梁识别等重要功能,常用的API…...

VUE3 ref 和 useTemplateRef
使用ref来绑定和获取 页面 <headerNav ref"headerNavRef"></headerNav><div click"showRef" ref"buttonRef">refbutton</div>使用ref方法const后面的命名需要跟页面的ref值一样 const buttonRef ref(buttonRef) cons…...

AWSLambda之设置时区
目标 希望Lambda运行的时区是东八区。 解决 只需要设置lambda的环境变量TZ为东八区时区即可,即Asia/Shanghai。 参考 使用 Lambda 环境变量...
