Java算法-一维前缀和与差分
一、一维前缀和
① 什么是一维前缀和?
📚 其实通过名字就能知道" 一维前缀和 "的意思:
通过一个一维数组"arr1"而创建的另一个一维数组"arr2","arr2"的每一个元素都是"arr1"的对应下标元素再加上该下标之前所有元素的和。
📕 简单的讲,可以理解为:每个位置的值是数组中该位置前的值的和。
让我们通过这个图片来看一下:

而一维前缀和一般都应用在什么地方呢?让我们看一道例题:
📖 给定一个长度为n的序列a,再给定q组查询,对于每次查询:
"给定一对l,r,你需要输出a数组中的l下标~r下标之间的和"
让我们看一下没有学过"一维差分"的暴力解题思想解题:
import java.util.*;public class Test {public static void main(String[] args) {Scanner scan = new Scanner(System.in);int n = scan.nextInt();int q = scan.nextInt();int[] arr = new int[n + 10];for(int i = 1;i <= n;i++) {arr[i] = scan.nextInt();}while(q-- > 0) {int l = scan.nextInt();int r = scan.nextInt();int num = 0;for(int i = l; i <= r;i++) {num += arr[i];}System.out.println(num);}}
}
那让我们来分析一下这样解题的时间复杂度:

数组的长度为'n',进行'q'次查询,若考虑最坏的情况,每次查询遍历整个数组,那么时间复杂度最坏的情况是O(nq)。
而该题中,n和q最大为1e5,那么O(nq)便能够达到可怕的(1e10),而我们要知道正常情况下,我们的编译器运算速度一秒也就是2e8,而1e10则是远远的超过了2e8:

果不其然,这是一定会超时的。
② 一维前缀和的使用
那么如果我们使用"一维前缀和"来进行解题,就能够大大的提高代码性能:
(为了使数组下标对应' l '和' r ',我们通常会从数组的1下标开始赋值:)


由图我们可以看出,在查询内部,我们之前的时间复杂度为O(r-l),而使用一维前缀数组后,将时间复杂度提升到了O(1)!!!这是非常大的提升~
用公式表示大概就是:l ~ r 的区间和等于"一维前缀和数组 arr2[r] - arr2[l - 1]";
📚 一维前缀和解题代码:
import java.util.*;public class Test {public static void main(String[] args) {Scanner scan = new Scanner(System.in);int n = scan.nextInt();int q = scan.nextInt();int[] arr1 = new int[n + 10];int[] arr2 = new int[n + 10];for(int i = 1;i <= n;i++) {//原数组arr1[i] = scan.nextInt();//一维前缀和数组arr2[i] = arr1[i] + arr2[i - 1];}while(q-- > 0) {int l = scan.nextInt();int r = scan.nextInt();System.out.println(arr2[r] - arr2[l - 1]);}}
}
经过改良后,也成功通过啦~
小练习:区间次方和(⭐)
问题描述:
给定一个长度为 n 的整数数组 a 以及 m 个查询。
每个查询包含三个整数 l,r,k 表示询问 l∼r 之间所有元素的 k 次方和。
请对每个查询输出一个答案,答案对 1e9+7 取模。
输入格式:
第一行输入两个整数 n,m 其含义如上所述。
第二行输入 n 个整数 a[1],a[2],...,a[n]。
接下来 m 行,每行输入三个整数 l,r,k 表示一个查询。
输出格式:
输出 m 行,每行一个整数,表示查询的答案对1e9+7取模的结果
📕 思路提示:
首先,看到对数组区间进行操作,我们就应该下意识地想到去使用"前缀和/差分"的方法来解题~
而每次操作,求对 l ~ r 之间所有元素的 k 次方求和,就很自然的应该去想到使用"前缀和"方法~

对元素的次方k只有1~5,数据并不庞大,也就意味着我们通过将1~5次方的数据全部求出来,放进一个前缀和数组中,然后通过输入的k来获取k次方,l~r代表访问的下标~
📚 代码实现:
import java.util.*;public class Main {public static void main(String[] args) {Scanner scan = new Scanner(System.in);int n = scan.nextInt();int m = scan.nextInt();//储存原数组long[] a = new long[n + 10];//储存1~5次方前缀和数组long[][] s = new long[10][n + 10];//i代表第i个元素for (int i = 1; i <= n; i++) {a[i] = scan.nextInt();//j代表j次方for(int j = 1; j <= 5; j++) {//(1 ~ 5次方和)s[j][i] = (long)Math.pow(a[i],j) + s[j][i - 1];}}while(m-- > 0) {int l = scan.nextInt();int r = scan.nextInt();int k = scan.nextInt();long num = s[k][r] - s[k][l - 1];System.out.println(num % 1000000007);}}
}
没什么问题,也是成功通过啦~
(该题是一道基础题,但需要注意一点:别忘了最后答案要对 1e9+7 取模哦~)
📚 一维前缀和的作用:
📕 一维前缀和的应用非常广泛,特别是在处理数组区间和的问题时非常有用
📕 通过计算数组的前缀和,我们可以在O(1)的时间复杂度内获得任意区间的和
二、一维差分
① 什么是一维差分?
📚 一维差分的定义:
一维差分是指对一个一维数组进行变换,使得原数组中连续元素之间的差值保存在另一个数组中,这个数组称为差分数组。
用图表示:

📚 那么一维差分的作用又是什么呢?同样的,让我们看一个小例题:
问题描述:
给定一个长度为n的序列a,再给定m组操作:
"每次操作给定3个正整数l,r,d,表示对a(l~r)中的所有数增加d"
最终输出操作结束后的序列 a
同样的,让我们看一下暴力解法:
📖 暴力解法的思路大概就是:
进行m组操作,每次操作都使用for循环,对(l~r)的区间进行遍历,并且依次将区间内的元素+d。
📚 代码实现:
import java.util.*;public class Test {public static void main(String[] args) {Scanner scan = new Scanner(System.in);int n = scan.nextInt();int m = scan.nextInt();int[] a = new int[n + 10];for(int i = 1;i <= n;i++) {a[i] = scan.nextInt();}while(m-- > 0) {int l = scan.nextInt();int r = scan.nextInt();int d = scan.nextInt();for(int i = l;i <= r;i++) {a[i] += d;}}for(int i = 1;i <= n;i++) {System.out.print(a[i] + " ");}}
}
同样的,和一维前缀和的例题一样,使用暴力解法会导致"超时"。
那么让我们来一起分析一下暴力解法的时间复杂度:

进行了"m"组操作,每次操作都对"l~r"的区间进行操作,我们假设最坏的情况,每次操作都遍历整个数组,也就是说时间复杂度等于O(mn),最大的时候也是能够到达1e10,仍然远远大于编译器一秒钟的运算(2e8)
② 一维差分的使用
📖 那么我们该如何改进呢?
让我们来看一下,一维差分的实现:
定义差分数组的公式:arr2[i] = arr1[i] - arr1[i - 1];
这个应该还是很好理解的,只需要前一项减去后一项就是两者之差~
而求差分数组,是为了对差分数组的首尾进行修改,然后再还原数组,从而达到将"m"次操作中的时间复杂度O(n)减小成O(1)~
具体我们还是看图:

由此,我们将之前的"从l~r位置进行遍历"改变成了"首尾进行操作",使O(nm)的时间复杂度减少成了O(m)。
📚 代码实现:
import java.util.*;
//1:无需package
//2: 类名必须Main, 不可修改public class Test {public static void main(String[] args) {Scanner scan = new Scanner(System.in);int i = 0;int a = scan.nextInt();int b = scan.nextInt();int[] arr1 = new int[a + 3];int[] arr2 = new int[a + 3];int[] arr3 = new int[a + 3];for(i = 1;i <= a;i++){arr1[i] = scan.nextInt();arr2[i] = arr1[i] - arr1[i - 1];}for(i = 0;i < b;i++){int n1 = scan.nextInt();int n2 = scan.nextInt();int n = scan.nextInt();arr2[n1] = arr2[n1] + n;arr2[n2 + 1] = arr2[n2 + 1] - n;}for(i = 1;i <= a;i++){arr2[i] = arr2[i] + arr2[i - 1];//c1 = a1 + c0(0)//c2 = a2 + c1(a1)//c3 = a3 + c2(a1 + a2)}for(i = 1;i <= a;i++){System.out.print(arr2[i] + " ");}}
}
也是成功通过了所有测试用例~并无超时现象~
小练习:小蓝的操作(⭐⭐)
问题描述:
一个数组 a 中共包含 n 个数,问最少多少次操作,可以让 a 数组所有数都变成 1 。
操作的内容是:
每次操作可以任选一个区间使得区间内的所有数字减 1 。 数据保证一定有解。
📚 思路分析:
同样的,看到对数组区间进行操作,下意识想到使用(前缀和/差分)进行求解,而此题问"需要多少次操作使得a[]数组中所有数变成1",显然是对数组内容进行了操作,于是便选择使用"差分"。
想要使得所有的数都变成1,那么最后我们得到的"差分数组"一定就是:

📖 这样的一个数组,其原理是:
第一个数字为1,而后面的元素,每一位都与前一位相等,也就是相当于"全为1"。

我们来用他的样例输入进行一下讲解:

📚 代码实现:
import java.util.*;public class Main {public static void main(String[] args) {Scanner scan = new Scanner(System.in);int a = scan.nextInt();int num = 0;int[] arr1 = new int[a + 5];int[] arr2 = new int[a + 5];for (int i = 1; i <= a; i++) {arr1[i] = scan.nextInt();arr2[i] = arr1[i] - arr1[i - 1];}for(int i = 1;i <= a;i++) {if(arr2[i] > 0) {num += arr2[i];}}System.out.println(num - 1);}
那么这次关于"一维前缀和与差分"就为大家分享到这里啦~有什么讲解不清楚或者需要修正的地方,还请大家多多在评论区指出,我这个小白也会虚心改正的~那我们下次再见啦
相关文章:

Java算法-一维前缀和与差分
一、一维前缀和 ① 什么是一维前缀和? 📚 其实通过名字就能知道" 一维前缀和 "的意思: 通过一个一维数组"arr1"而创建的另一个一维数组"arr2","arr2"的每一个元素都是"arr1"…...

Elasticsearch 安装教程:驾驭数据海洋的星际导航仪
目录 一、准备工作1. ES的下载 二、安装步骤三、注意事项四、启动报错1. org.elasticsearch.bootstrap.StartupException: java.lang.RuntimeException: can not run elasticsearch as root2. max virtual memory areas vm.max_map_count [65530] is too low, increase to at l…...

【解决方案】微信小程序如何使用 ProtoBuf 进行 WebSocket 通信
前言 故事背景 简单说下背景,项目中需要用 ProtoBuf 协议转换请求参数,并通过 WebSocket 进行双向通信。重点!一个是 web端(Vue3 TS),一个是微信小程序端(原生 JS)。 剧情发展 …...

独立游戏开发者面临的挑战与困境
在当今竞争激烈的游戏市场中,独立游戏开发者面临着诸多挑战与困境。从游戏版号申请到游戏被抄袭,再到产品同质化以及流量获取难题,乃至外包内卷现象,每一个环节都考验着开发者的智慧与毅力。以下是对这些挑战与闲境的详细分析。 …...

KVM 虚拟机Anolis OS 8.9 下利用宝塔面板中的 Docker 配置 Nextcloud + onlyoffice
第一部分:安装配置 nextcloud 准备 (1)启动一个 Anolis OS 8.9 虚拟机,见下图。该虚拟机为 anlisos8…0.2 虚拟机的 ssh、hostname 、IP地址都已配置好。 (2)宝塔面板也已安装好docker 一、环境 do…...

串口扫盲TTL,TX/TR/GND
1. 串口扫盲TTL,TX/TR/GND 1. 串口扫盲TTL,TX/TR/GND 1.1. TTL1.2. USB转TTL1.3. 串口通信1.4. 引脚缩写1.5. 参考资料 1.1. TTL TX(TXD) 来源于 Transmit 一词,意思为发送,发射RX(RXD) 来源于 Receive 一词 意思为接收,收到GND 地线&…...

Python酷库之旅-第三方库Pandas(181)
目录 一、用法精讲 836、pandas.api.types.is_file_like函数 836-1、语法 836-2、参数 836-3、功能 836-4、返回值 836-5、说明 836-6、用法 836-6-1、数据准备 836-6-2、代码示例 836-6-3、结果输出 837、pandas.api.types.is_list_like函数 837-1、语法 837-2、…...

Python数据分析NumPy和pandas(十七、pandas 二进制格式文件处理)
以二进制格式存储(或序列化)数据的一种简单方法是使用 Python 的内置 pickle 模块。同时,pandas 构造的对象都有一个 to_pickle 方法,该方法以 pickle 格式将数据写入磁盘。 我们先把之前示例用到的ex1.csv文件加载到pandas对象中…...

matlab计算相关物理参数
function Rx1Jetfire1_1(di,Ct,Tf,Tj,alpha,Ma,Mf,RH,P0,P,k,Cd,elta,deltaHc,tau,directory) % 一共15个独立变量,为了方便输入修改,所有变量存入Jetfire1_1excel表, % dj为孔口直径,m;Ct为燃料空气混合摩尔系数,可…...

nmcli、ip、ifcfg配置网络区分方法
文章目录 一、检查NetworkManager状态使用nmcli命令:检查NetworkManager服务状态: 二、检查ip命令的使用三、检查ifcfg文件查看/etc/sysconfig/network-scripts/目录:查看/etc/network/interfaces文件(针对Debian系)&a…...

第四届智能电力与系统国际学术会议(ICIPS 2024)
文章目录 一、会议详情二、重要信息三、大会介绍四、出席嘉宾五、征稿主题六、咨询 一、会议详情 二、重要信息 大会官网:https://ais.cn/u/vEbMBz提交检索:EI Compendex、IEEE Xplore、Scopus 三、大会介绍 四、出席嘉宾 五、征稿主题 如想"投稿…...

区块链样题第4套解析 后端应用开发部分
任务3-2:区块链应用后端开发 使用JAVA-SDK与区块链进行交互,通过solc2Java工具将Solidity智能合约转译为可供Java调用的文件,实现区块链编程。 前言:题目只是单纯考了对于fisco-java-sdk的简单使用 教程参考: 1.这边建议还是学习完JavaWeb课程。 黑马程序员JavaWeb...

C语言实现408考研真题2016年43题
#include <iostream> // 定义分区函数,返回两个子数组之和的差值 int setPartition(int a[], int n) { int pivotkey, low 0, low0 0, high n - 1, high0 n - 1, flag 1, k n / 2, i; int s1 0, s2 0; // 当low等于k-1,…...

2024年,Rust开发语言,现在怎么样了?
Rust开发语言有着一些其他语言明显的优势,但也充满着争议,难上手、学习陡峭等。 Rust 是由 Mozilla 主导开发的通用、编译型编程语言,2010年首次公开。 在 Stack Overflow 的年度开发者调查报告中,Rust 连续多年被评为“最受喜爱…...

三种网络配置方法nmcli、ip、ifcfg文件
文章目录 总结nmcli配置网络定义与功能:特点:示例: ip配置网络定义与功能:特点:示例: ifcfg配置网络定义与功能:特点:示例: 总结 nmcli:适合需要动态管理网络…...

AES_ECB算法C++与Java相互加解密Demo
一、AES算法 AES是一种对称加密算法,算法秘钥长度可为128位(16字节)、192位(24字节)、256位(32字节)。加密模式分为ECB、CBC、CTR等,其中ECB模式最简单够用。现给出ECB模式下C和Java的实现,并且可以相互加解密验证。 二、AES_ECB实现DEMO …...

H7-TOOL自制Flash读写保护算法系列,为兆易创新GD32E23X制作使能和解除算法,支持在线烧录和脱机烧录使用(2024-10-29)
说明: 很多IC厂家仅发布了内部Flash算法文件,并没有提供读写保护算法文件,也就是选项字节算法文件,需要我们制作。 实际上当前已经发布的TOOL版本,已经自制很多了。但是依然有些厂家还没自制,所以陆续开始…...

FFmpeg 深度教程音视频处理的终极工具
1. 引言 什么是 FFmpeg? FFmpeg 是一个开源的跨平台多媒体处理工具,广泛应用于音视频的录制、转换、流式传输以及编辑等多个领域。它由 FFmpeg 项目团队开发和维护,支持几乎所有主流的音视频格式和编解码器。FFmpeg 包含了一系列强大的命令…...
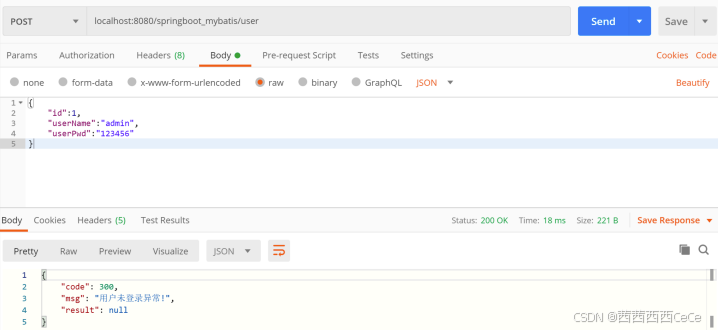
Java程序设计:spring boot(13)——全局异常与事务控制
1 Spring Boot 事务支持 在使⽤ Jdbc 作为数据库访问技术时,Spring Boot框架定义了基于jdbc的PlatformTransaction Manager 接⼝的实现 DataSourceTransactionManager,并在 Spring Boot 应⽤ 启动时⾃动进⾏配置。如果使⽤ jpa 的话 Spring Boot 同样提供…...

金和OA-C6 ApproveRemindSetExec.aspx XXE漏洞复现(CNVD-2024-40568)
0x01 产品描述: 金和C6协同管理平台是以"精确管理思想"为灵魂,围绕“企业协同四层次理论”模型,并紧紧抓住现代企业管理的六个核心要素:文化 Culture、 沟通Communication 、 协作Collaboration 、创新 Creation、 控制…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...
