数据结构和算法-动态规划(3)-经典问题

动态规划常见问题

打家劫舍

题目

[力扣198] 198. 打家劫舍 - 力扣（LeetCode）

题目描述

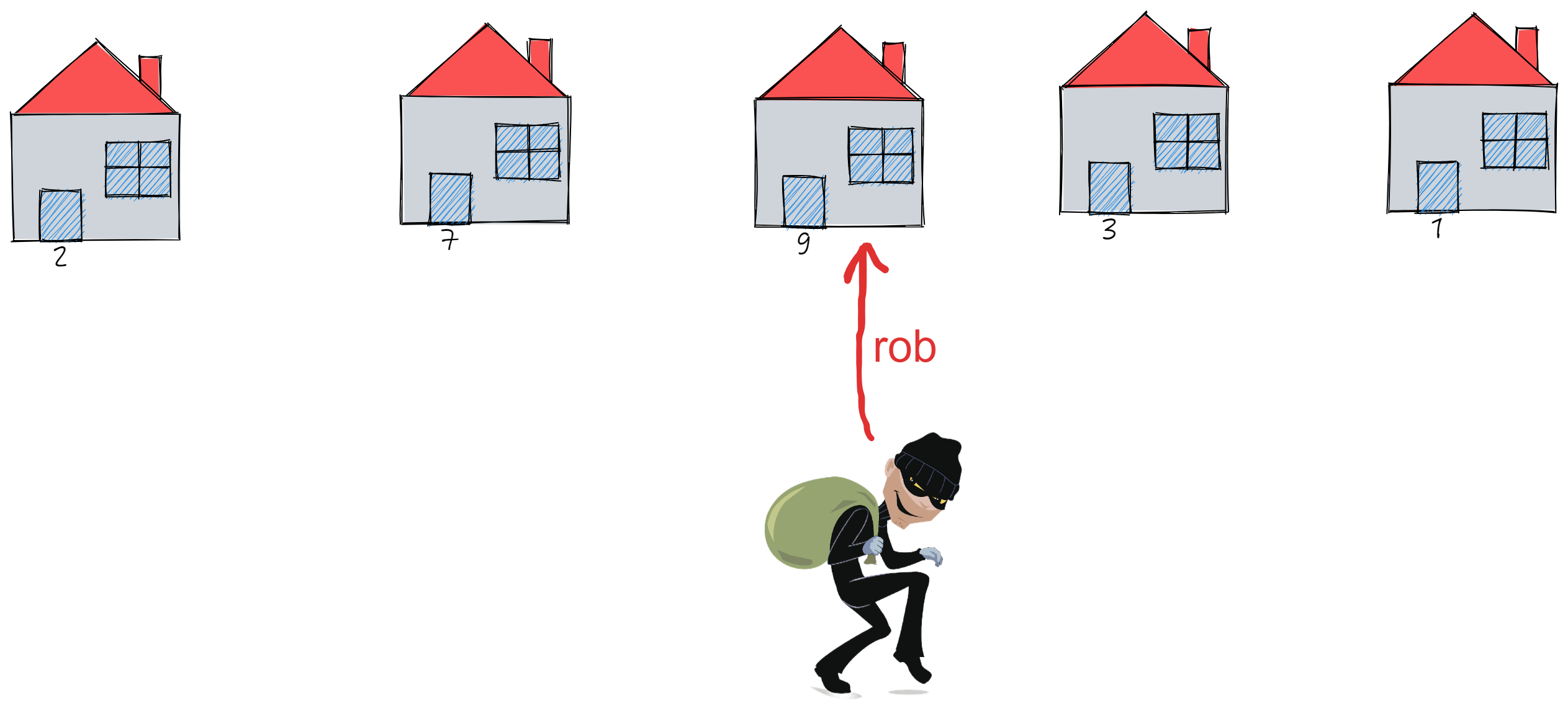
你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

示例 1：

输入：[1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。

示例 2：

输入：[2,7,9,3,1]
输出：12
解释：偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。偷窃到的最高金额 = 2 + 9 + 1 = 12 。

解决方案

边界条件

• 只有一间房子

  

  if(nums.length==1) return nums[0];
  

• 有2间房子

  

  if (nums.length == 2)
  return Math.max(nums[0],nums[1]);
  

一般情况

• 定义记忆化数组int[] , 记录每次偷窃成功的值。

  int[] dp = new int[nums.length];
  

• 初始化dp(1间房子或两间房子)

  dp[0] = nums[0];
  dp[1] = Math.max(nums[0],nums[1]);
  

• 其它情况

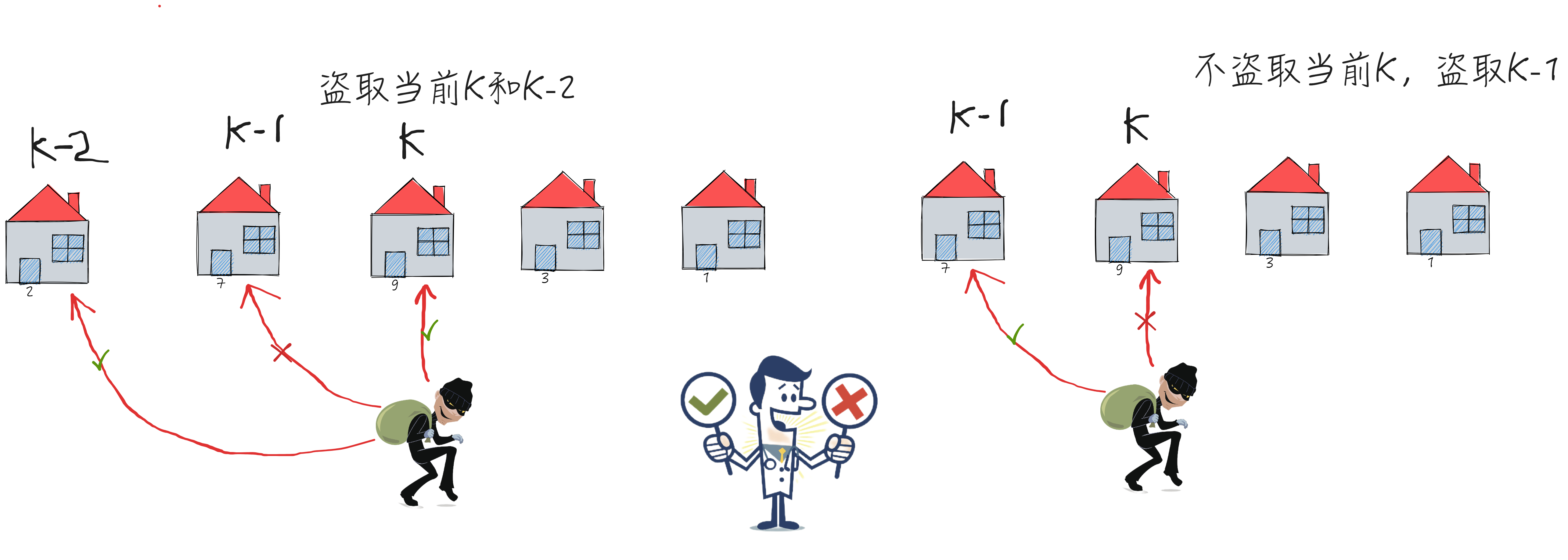
  • 当前盗取的第K个房间的结果与 前K-2 个有关
  • 如果不选择盗取当前K，则与K-1有关

  //状态转移方程
  dp[K] = max(dp[K-2] + nums[K], dp[K-1]);
  

  tips： 不能盗取相邻的房子

  

  for (int i = 2; i < nums.length; i++) {dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1]);
  }
  

  提交模版

  class Solution {public int rob(int[] nums) {}
  }
  

  参考实现

  class Solution {public int rob(int[] nums) {// 定义dp数组，存储最优结果int[] dp = new int[nums.length];if (nums.length == 1) {return nums[0];}/** 边界条件: 只有两间房子*/dp[0] = nums[0];dp[1] = Math.max(nums[0], nums[1]);/** 状态转移方程*/for (int i = 2; i < nums.length; i++) {dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1]);}return dp[dp.length - 1];}
  }
  

打家劫舍II

题目

[力扣213] 213. 打家劫舍 II - 力扣（LeetCode）

题目描述

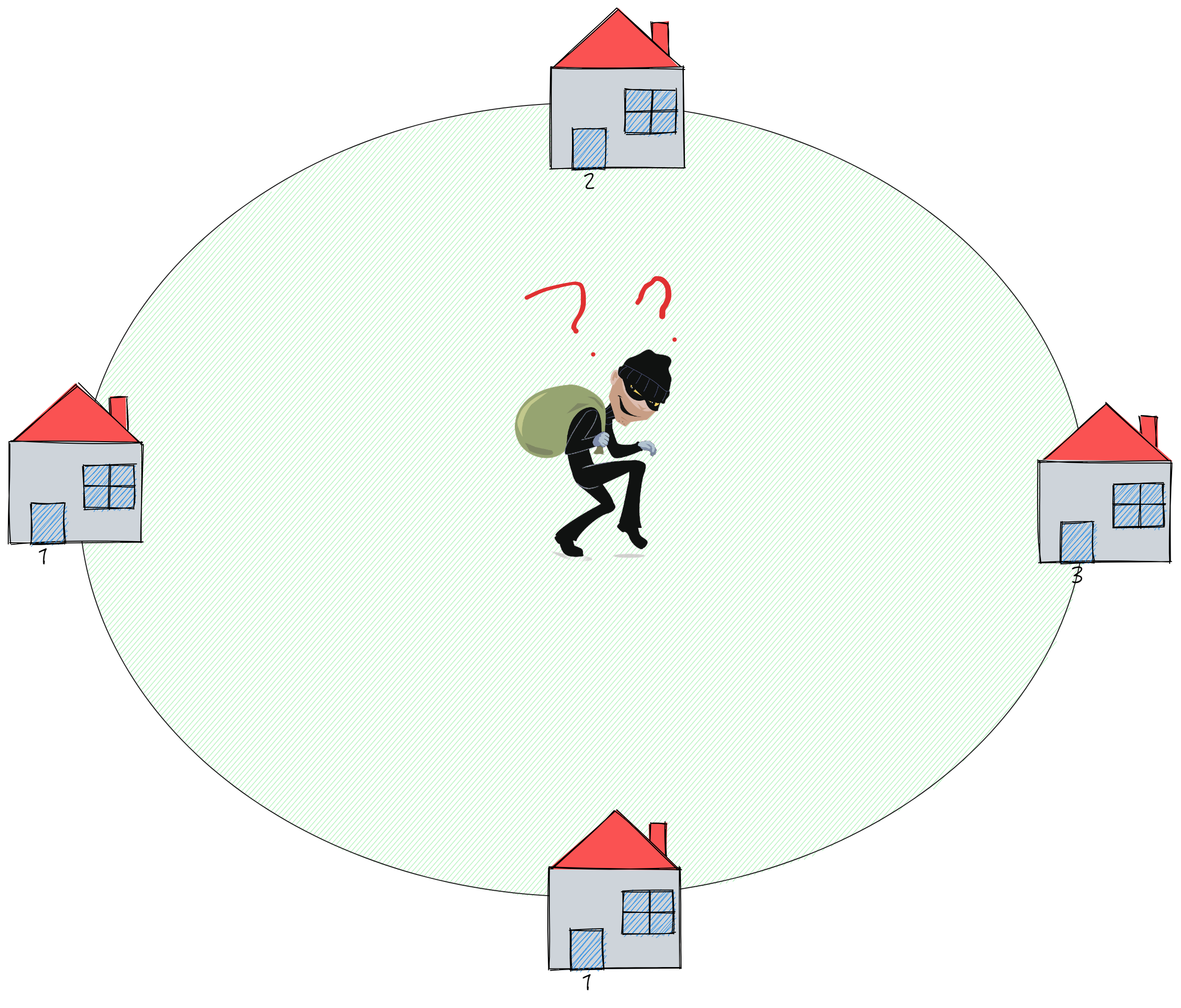
你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警 。

给定一个代表每个房屋存放金额的非负整数数组，计算你 在不触动警报装置的情况下 ，今晚能够偷窃到的最高金额。

示例 1：

输入：nums = [2,3,2]
输出：3
解释：你不能先偷窃 1 号房屋（金额 = 2），然后偷窃 3 号房屋（金额 = 2）, 因为他们是相邻的。

示例 2：

输入：nums = [1,2,3,1]
输出：4
解释：你可以先偷窃 1 号房屋（金额 = 1），然后偷窃 3 号房屋（金额 = 3）。偷窃到的最高金额 = 1 + 3 = 4 。

示例 3：

输入：nums = [1,2,3]
输出：3

解决方案

边界条件

• 只有一间房子

  

  if(nums.length==1) return nums[0];
  

• 有2间房子

  

  if (nums.length == 2)
  return Math.max(nums[0],nums[1]);
  

一般条件

提交模版

参考实现

class Solution {public int rob(int[] nums) {if (nums.length == 1) {return nums[0];} else if (nums.length == 2) {return Math.max(nums[0], nums[1]);} else {int a = robRange(nums, 0, nums.length - 1);int b = robRange(nums, 1, nums.length);return Math.max(a, b);}}public int robRange(int[] nums, int start, int end) {int[] a =  Arrays.copyOfRange(nums,start, end);int pre = 0;int curr = 0;int tmp = 0;for(int i =0 ;  i< a.length; i++){tmp = curr;curr = Math.max(pre + a[i], curr);pre = tmp;}return curr;}
}

子串问题

问题

两组字符串 X=“ATCTGAT”, Y= “TGCATA”, 找出相同的子字符串，且顺序不变Z=“TCAT”, 长度4。

分析

检查X，Y较小的字符串看看它们的最长子串，分成两类最后一个字符相同，最后一个字符不同

如果其中一个字符串为空

如果X，Y中任意一个字符串为空，那么不存在最长子串问题

最长子串 = 0 ;    X,y的字符串为空

从较小的问题看-末尾不同

• Y不变，看X的较小字符串"ATCTGA"

  X = “ATCTGAT” 是由X1=“ATCTGA” 和“T"构成，看看X1 和Y的最大子串。“TCTA”

  

• X不变， 看Y的较小字符串"TGCATA"

  X=“ATCTGAT”, Y1=“TGCAT”，最大子串 “TCAT"

  

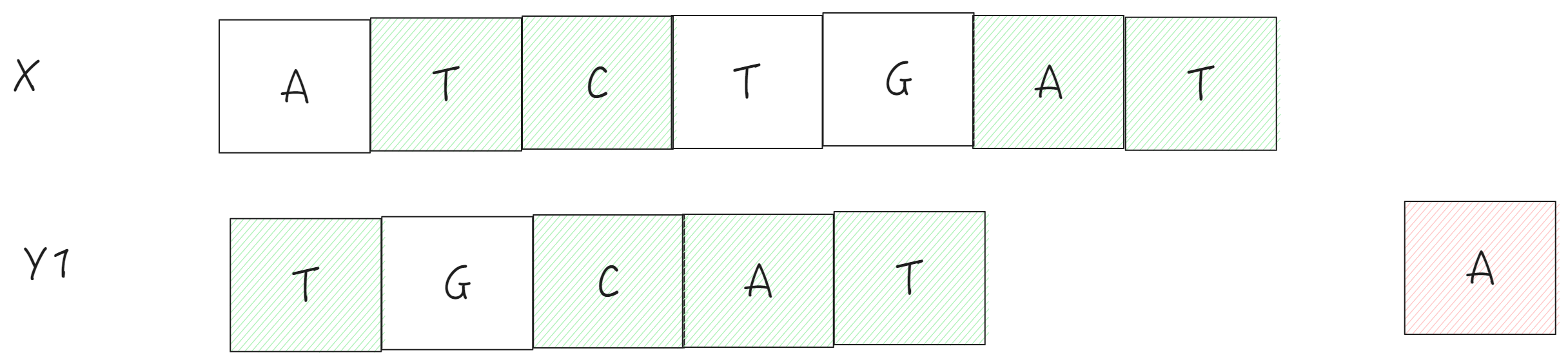
• 最大相同子串

  假设X字符串当前的索引为 i；Y字符串的索引为j。

  最大长度 = max(X之前的最大字符串, Y之前的字符串)
  

末尾相同

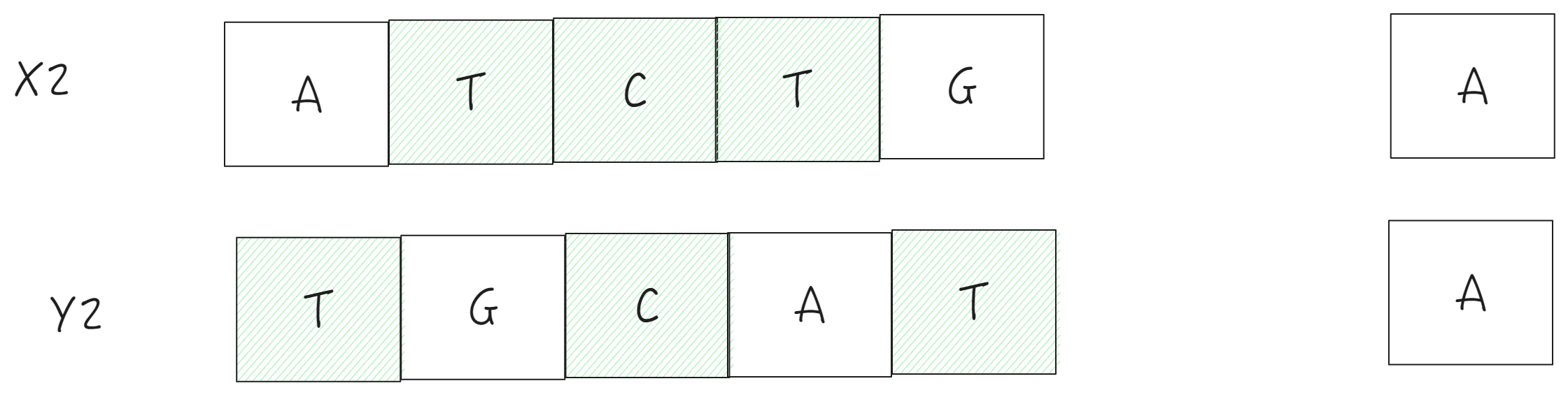
最长子串就是之前的最大子串+当前的相同字符

最大子串 = 之前的最大子串+1

解决方案

由分析可得，最大子串可以分为3中情况,使用int[][] dp数组记忆化步骤。

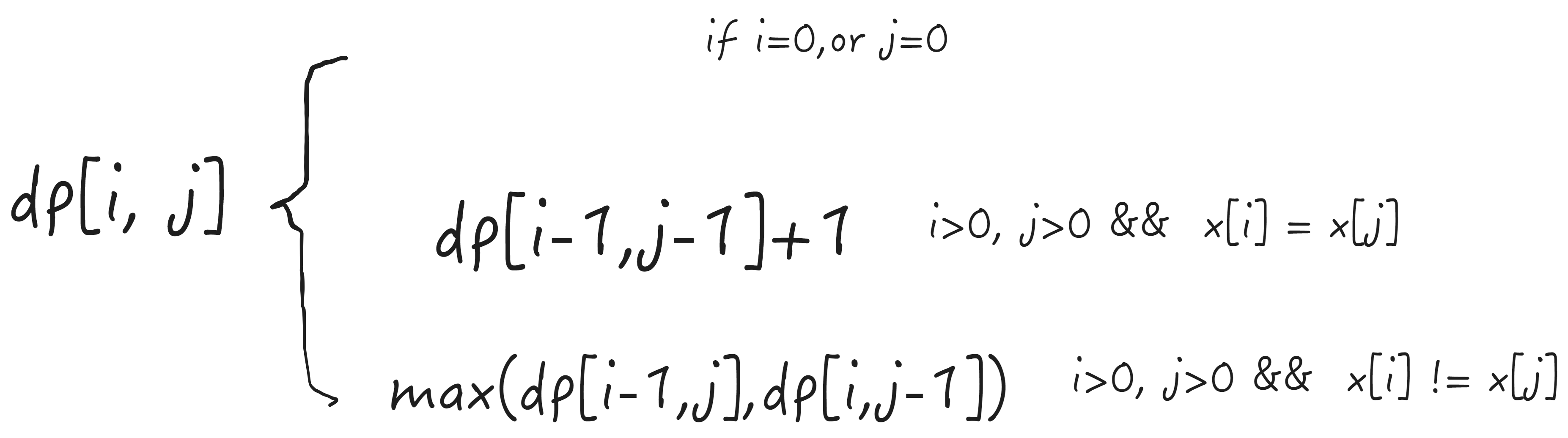
package com.ffyc.dp;public class SubString {public static void main(String[] args) {String x = "ATCTGAT";String y = "TGCATA";int len1 = x.length();int len2 = y.length();int result = 0;if(len1==0|| len2 ==0) result = 0;int[][] dp = new int[len1][len2];for(int i=0; i< len1;i++){for(int j =0; j<len2;j++){if(i!=0 && j!=0){if(x.charAt(i) == y.charAt(j)){dp[i][j] = dp[i-1][j-1]+1;}else{dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);}}else{dp[i][j] = x.charAt(i)== y.charAt(j) ? 1 :0;}}}result = dp[len1-1][len2-1];System.out.println(result);}
}

买卖股票

买卖股票的最佳时机

题目

[力扣121] 121. 买卖股票的最佳时机 - 力扣（LeetCode）

描述

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

解决方案

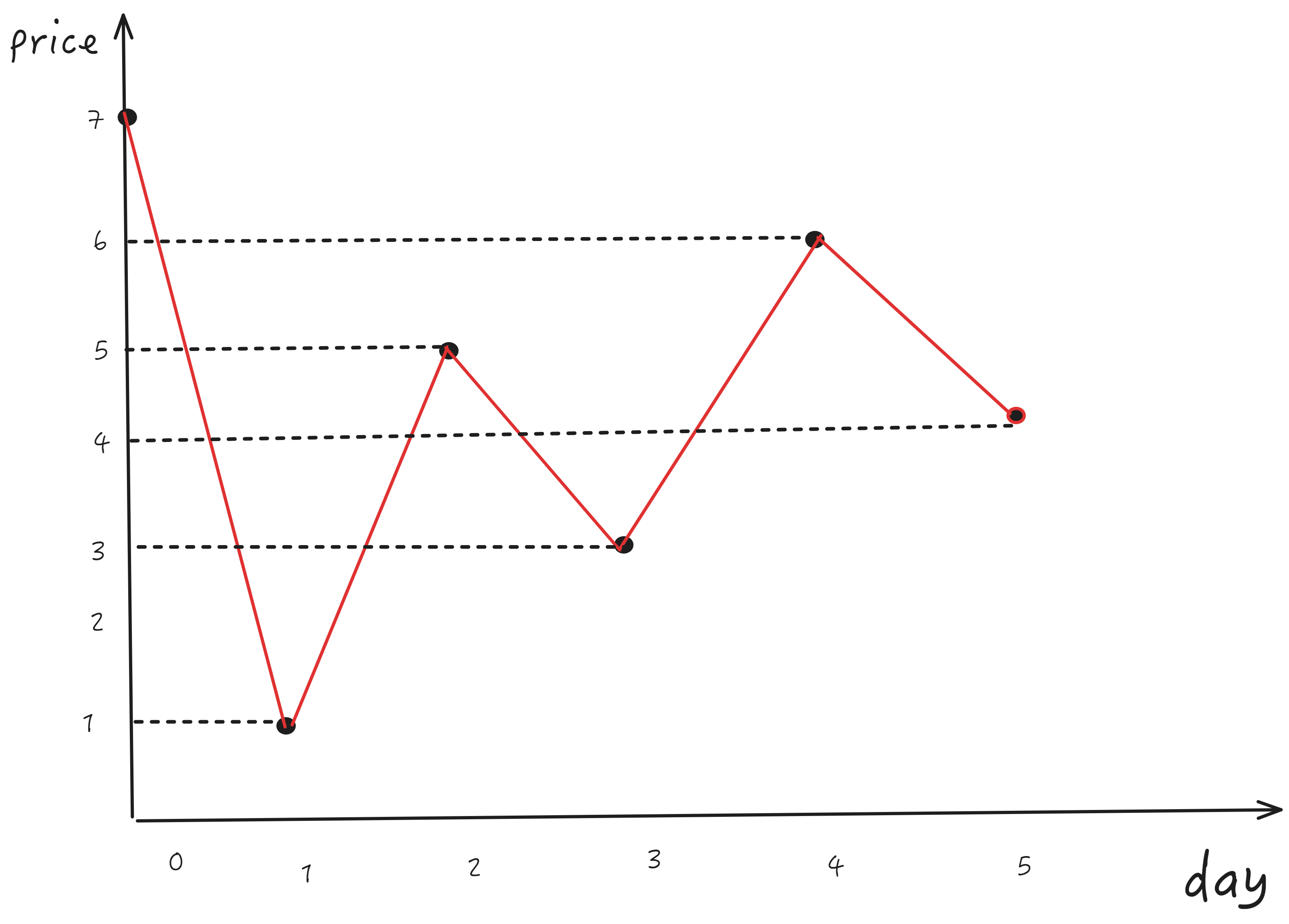
有两个因素影响股票价格

• 当天不卖，前一天的股票最大价格

  dp[d] = dp[d-1]; //d表示当天
  

• 当天卖出某一天买入的最小价格，比如上周五买最低，本周二卖

  dp[d] = price[d]- min(dp[从开始--当天的最小值]);
  

动态转移方程

dp[i] = max(dp[i-1],  price[i]-min(dp[从开始--当天的最小值]));

提交模版

class Solution {public int maxProfit(int[] prices) {}
}

参考实现

class Solution {public int maxProfit(int[] prices) {int n = prices.length;if (n < 2)return 0;int[] dp = new int[n];int min = prices[0];for(int i=1; i < n;i++){dp[i] = Math.max(dp[i-1], prices[i]-min);min = Math.min(min, prices[i]);}return dp[n-1];}
}

买卖股票的最佳时机II

问题

[力扣122]122. 买卖股票的最佳时机 II - 力扣（LeetCode）

问题描述

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。

返回 你能获得的 最大 利润 。

示例 1：

输入：prices = [7,1,5,3,6,4]
输出：7
解释：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3。
最大总利润为 4 + 3 = 7 。

示例 2：

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
最大总利润为 4 。

示例 3：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 交易无法获得正利润，所以不参与交易可以获得最大利润，最大利润为 0。

解决方案

当天i, 有两种最大股票利润的状态，

• 持有此股票的最大利润
• 不持有此股票的最大利润

用二维数组创建记录数组： dp[天][是否持有股票] —0:不持有股票， 1：持有股票

tips: 可以当天买入当天卖出

• 当天不持有

  • 前一天卖出，不持有

    dp[i-1][0]
    

  • 前一天买入，当天卖出，不持有,今天就可以盈利

    dp[i-1][1]+prices[i];
    

• 当天持有

  • 前一天买入

    dp[i-1][1];
    

  • 前一天没有，当天买入,减去今天花费的成本

  dp[i-1][0]-price[i];
  

参考实现

class Solution {public int maxProfit(int[] prices) {int n = prices.length;if(n < 2) return 0;int[][] dp = new  int[n][2];dp[0][1] = 0- prices[0]; //当天成为买入成本for(int i=1; i<n;i++){dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1]+prices[i]);dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0]-prices[i]);}return dp[n-1][0];}
}