数据结构+算法
一、数据结构
1、线性结构
- 数组:
- 访问:O(1)访问特定位置的元素;
- 插入:O(n)最坏的情况发生在插入发生在数组的首部并需要移动所有元素时;
- 删除:O(n)最坏的情况发生在删除数组的开头发生并需要移动第一元素后面所有的元素时
- 链表:使用的不是连续的内存空间来存储数据。
- 链表的插入和删除操作的复杂度为 O(1) ,只需要知道目标位置元素的上一个元素即可。但是,在查找一个节点或者访问特定位置的节点的时候复杂度为 O(n) 。
- 数组链表比较:
- 数组支持随机访问,而链表不支持。
- 数组使用的是连续内存空间对 CPU 的缓存机制友好,链表则相反。
- 数组的大小固定,而链表则天然支持动态扩容。如果声明的数组过小,需要另外申请一个更大的内存空间存放数组元素,然后将原数组拷贝进去,这个操作是比较耗时的
- 栈
- 允许在有序的线性数据集合的一端(称为栈顶 top)进行加入数据(push)和移除数据(pop),后进先出(LIFO, Last In First Out),push 和 pop 的操作都发生在栈顶。
- 队列
- 先进先出 (FIFO,First In, First Out) 的线性表。通常用链表或者数组来实现,用数组实现的队列叫作 顺序队列 ,用链表实现的队列叫作 链式队列 。队列只允许在后端(rear)进行插入操作也就是入队 enqueue,在前端(front)进行删除操作也就是出队 dequeue
2、图

- 概念
- 顶点:图中的数据元素,图至少有一个顶点(非空有穷集合)
- 边:顶点之间的关系用边表示
- 度:表示一个顶点包含多少条边,在有向图中,还分为出度和入度,出度表示从该顶点出去的边的条数,入度表示进入该顶点的边的条数。
- 无向图、有向图:边表示的是顶点之间的关系,有的关系是双向的,有的是单向的
- 无权图、带权图:边是否具有权重
- 图的存储
- 邻接矩阵存储:邻接矩阵将图用二维矩阵存储,是一种较为直观的表示方式。如果第 i 个顶点和第 j 个顶点之间有关系,且关系权值为 n,则
A[i][j]=n。在无向图中,当顶点 i 和顶点 j 有关系时,A[i][j]=1,无关系时,A[i][j]=0。(比较浪费空间)
- 无向图的邻接矩阵是一个对称矩阵,因为在无向图中,顶点 i 和顶点 j 有关系,则顶点 j 和顶点 i 必有关系。
- 邻接表存储:使用一个链表来存储某个顶点的所有后继相邻顶点。对于图中每个顶点 Vi,把所有邻接于 Vi 的顶点 Vj 链成一个单链表,这个单链表称为顶点 Vi 的 邻接表。

- 在无向图中,邻接表元素个数等于边的条数的两倍;在有向图中,邻接表元素个数等于边的条数
- 邻接矩阵存储:邻接矩阵将图用二维矩阵存储,是一种较为直观的表示方式。如果第 i 个顶点和第 j 个顶点之间有关系,且关系权值为 n,则
- 图的搜索:BFS、DFS
3、堆
- 定义:堆是一种满足以下条件的树:堆中的每一个节点值都大于等于(或小于等于)子树中所有节点的值。或者说,任意一个节点的值都大于等于(或小于等于)所有子节点的值。(可以看成是近似的完全二叉树)
- 用途:当我们只关心所有数据中的最大值或者最小值,存在多次获取最大值或者最小值,多次插入或删除数据时,就可以使用堆。
- 时间复杂度:插入和删除操作O(lgn),堆初始化时间复杂度O(n)
- 分类:大根堆、小根堆
- 存储:由于完全二叉树的性质,利用数组存储二叉树即节省空间,又方便索引(若根结点的序号为0,那么对于树中任意节点 i,其左子节点序号为
2*i + 1,右子节点序号为2*i+2) - 堆的操作(大根堆):
- 插入:先将元素放至数组末尾,再自底向上堆化,将末尾元素上浮

- 删除堆顶:删除堆顶元素,将末尾元素放至堆顶,再自顶向下堆化,将堆顶元素下沉
-

- 插入:先将元素放至数组末尾,再自底向上堆化,将末尾元素上浮
- 堆排序:
- 第一步是建堆,将一个无序的数组建立为一个堆
- 最后一个节点的父结点及它之前的元素,都是非叶节点。即节点个数为 n,只需对 (n - 1) / 2 到 0 的节点进行自顶向下(沉底)堆化(顺序是从后往前堆化)

- 第二步是排序,将堆顶元素与最后位置元素交换,然后对剩下元素进行堆化,反复迭代
- 第一步是建堆,将一个无序的数组建立为一个堆
-
堆以及堆排序 class Solution {public int[] sortArray(int[] nums) { //若根结点的序号为0,那么对于树中任意节点 i,其左子节点序号为 2*i + 1,右子节点序号为 2*i+2 //初始堆化:从(n - 1)/2 到0,自顶向下堆化heapify(nums); //将堆顶元素与最后位置元素交换,然后对0位置进行堆化,反复迭代for (int j = nums.length - 1; j > 0; j--) {swap(j, 0, nums);siftDown(0, j, nums);}return nums;}private void heapify(int[] nums) {for (int i = (nums.length >>> 1) - 1; i >= 0; i--) {siftDown(i, nums.length, nums);}}//大根堆private void siftDown(int index, int len, int[] nums) {int half = len >>> 1;while (index < half) {int child = (index << 1) + 1;//左移运算符优先级低于加号int right = 1 + child;//获取左右节点中较大的子节点if (right < len && nums[child] < nums[right]) {child = right;}if (nums[index] >= nums[child]) {break;}//跟较大的子节点交换swap(index, child, nums);index = child;}}private void siftUp(int index, int[] nums) {while (index > 0) {int father = (index - 1) >>> 1;if (nums[father] > nums[index]) {break;}swap(father, index, nums);index = father;}}private void swap(int a, int b, int[] nums) {nums[a] ^= nums[b];nums[b] ^= nums[a];nums[a] ^= nums[b];}}
4、树
- 定义
- 二叉树分类
- 满二叉树:每一个层的结点数都达到最大值。或者如果一个二叉树的层数为 K,且结点总数是(2^k) -1 ,则它就是 满二叉树

- 完全二叉树:最后一层外,若其余层都是满的,并且最后一层是满的或者是在右边缺少连续若干节点。当根节点的值为 1 的情况下,若父结点的序号是 i,那么左子节点的序号就是 2i,右子节点的序号是 2i+1。

- 平衡二叉树:可以是一棵空树;如果不是空树,它的左右两个子树的高度差的绝对值不超过 1,并且左右两个子树都是一棵平衡二叉树。(红黑树、AVL数)
- 满二叉树:每一个层的结点数都达到最大值。或者如果一个二叉树的层数为 K,且结点总数是(2^k) -1 ,则它就是 满二叉树
- 存储
- 链式存储:

- 数组存储:顺序存储就是利用数组进行存储,数组中的每一个位置仅存储节点的 data,不存储左右子节点的指针,子节点的索引通过数组下标完成。根结点的序号为 0,对于每个节点 Node,假设它存储在数组中下标为 i 的位置,那么它的左子节点就存储在 2i + 1 的位置,它的右子节点存储在下标为 2i+2 的位置。
- 如果存储的二叉树不是完全二叉树,在数组中就会出现空隙,导致内存利用率降低
- 链式存储:
- 遍历
- 层序遍历:bfs
- 先序遍历

- 中序遍历

- 后序遍历

- morris遍历
5、红黑树
二、算法
1、算法思想
- 贪心:局部最优-->全局最优
- 动态规划:动态规划中每一个状态一定是由上一个状态推导出来
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 回溯-穷举
- 回溯函数返回值以及参数
- 回溯函数终止条件
- 回溯函数终止条件
- 分治
- 将一个规模为 N 的问题分解为 K 个规模较小的子问题,这些子问题相互独立且与原问题性质相同。求出子问题的解,就可得到原问题的解。
2、常见数据结构算法题目
3、字符串算法
4、常见链表算法
5、十大经典排序
6、经典剑指offer题目
相关文章:

数据结构+算法
一、数据结构 1、线性结构 数组: 访问:O(1)访问特定位置的元素;插入:O(n)最坏的情况发生在插入发生在数组的首部并需要移动所有元素时;删除:O(n)最坏的情况发生在删除数组的开头发生并需要移动第一元素后…...

利用ExcelJS封装一个excel表格的导出
ExcelJS 操作和写入Excel 文件。 直接上代码,js部分: exportFn.js import ExcelJS from exceljs; import { saveAs } from file-saver;export function exportExcleUtils(tHeader, filterVal, listData, fileName) {//设置工作簿属性const workbook ne…...

AI 原生时代,更要上云:百度智能云云原生创新实践
本文整理自百度云智峰会 2024 —— 云原生论坛的同名演讲。 我今天分享的主题,是谈谈在云计算和 AI 技术快速发展和深入落地的背景下,百度智能云在云原生的基础设施产品和技术层面做的一些创新实践。 毋庸置疑,过去十几年云计算和 AI 技术是…...

C语言程序编译运行
程序功能:使用 printf() 输出 “Hello, World!”。 C语言源程序: #include <stdio.h> int main() {// printf() 中字符串需要引号printf("Hello, World!");return 0; }编译过程: vim hello.c gcc hello.c -o hello ./hell…...

视频点播系统扩展示例
更多的前端页面(如视频详情页、用户注册页等)。更复杂的业务逻辑(如视频评论、搜索功能等)。安全性和权限管理(如用户角色管理、权限控制等)。其他技术细节(如文件上传、分页查询等)…...

echo $? —— Linux 中的退出状态码详解
在 Linux 系统中,echo $? 是一个非常重要的命令,用于显示上一条命令的退出状态码。这个小小的符号组合可以帮助我们判断命令是否成功执行,同时也为编写自动化脚本提供了基础支持。本文将详细介绍 echo $? 的用法及其在实际开发中的应用。 …...
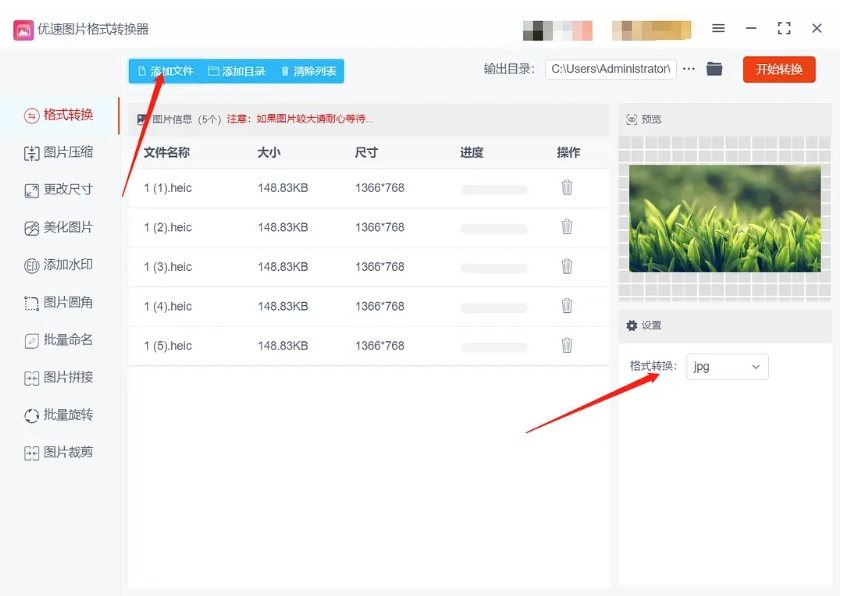
heic格式转化jpg最简单方法?快来学习这几种简单的转换方法!
heic格式转化jpg最简单方法?在当今的数字图像处理领域,HEIC格式以其卓越的压缩效率和高质量图像表现,正逐渐崭露头角并受到业界的深切关注,HEIC格式凭借先进的压缩技术,成功地在保持图像清晰度的同时,大幅度…...
力扣(leetcode)每日一题 3259 超级饮料的最大强化能量|动态规划
3259. 超级饮料的最大强化能量 题干 来自未来的体育科学家给你两个整数数组 energyDrinkA 和 energyDrinkB,数组长度都等于 n。这两个数组分别代表 A、B 两种不同能量饮料每小时所能提供的强化能量。 你需要每小时饮用一种能量饮料来 最大化 你的总强化能量。然而…...

Webserver(2.7)内存映射
目录 内存映射内存映射相关系统调用内存映射的注意事项如果对mmap的返回值(ptr)做操作,释放内存(munmap)是否能够成功?如果open时O_RDONLY,mmap时prot参数指定PROT_READ | PROT_WRITE会怎样?如果文件偏移量…...

vue3父子组件传值,子组件暴漏方法
1.父传子 defineProps 父组件直接通过属性绑定的方式给子组件绑定数据,子组件通过defineProps接收函数接收 其中v-model是完成事件绑定和事件监听的语法糖。v-model算是v-bind和v-on的简洁写法,等价于 <c-input ref"inputRef" :modelValue…...

Linux_04 Linux常用命令——tar
一、命令格式 tar [选项] [归档文件] [要处理的文件或目录]1、选项 c创建归档文件x解压缩归档文件z使用gzipj使用bzip2v处理过程显示信息f指定归档文件名称 2、归档文件-可指定目录及文件名 /home/wang.tar.gz 3、要处理的文件或目录 /home/study1/wang 二、常见命令 t…...

Java项目实战II基于Java+Spring Boot+MySQL的编程训练系统(源码+数据库+文档)
目录 一、前言 二、技术介绍 三、系统实现 四、文档参考 五、核心代码 六、源码获取 全栈码农以及毕业设计实战开发,CSDN平台Java领域新星创作者,专注于大学生项目实战开发、讲解和毕业答疑辅导。获取源码联系方式请查看文末 一、前言 在当今数字…...

Rust:文档注释 //! 和 ///
在 Rust 编程语言中,//! 是一种特殊的文档注释(documentation comment)。它用于为整个模块、结构体、枚举、函数或其他项提供文档说明。与单行注释 // 和多行注释 /* ... */ 不同,//! 和 ///(用于紧跟在项之前的文档注…...

练习LabVIEW第二十七题
学习目标: 刚学了LabVIEW,在网上找了些题,练习一下LabVIEW,有不对不好不足的地方欢迎指正! 第二十七题: 创建一个VI程序模拟温度测量。假设传感器输出电压与温度成正比。例如,当温度为70F时&…...
使用React构建现代Web应用
💖 博客主页:瑕疵的CSDN主页 💻 Gitee主页:瑕疵的gitee主页 🚀 文章专栏:《热点资讯》 使用React构建现代Web应用 1 引言 2 React简介 3 安装React 4 创建React项目 5 设计应用结构 6 创建组件 7 使用组件…...

【系统设计】Merkle 算法在 Git 中的应用:深入理解与实践
引言 在现代软件开发中,Git 已成为版本控制的事实标准。Git 能够快速处理项目的变化,确保代码的完整性,其中一个关键技术就是 Merkle 树。本文将深入探讨 Merkle 算法的原理,以及其在 Git 中的具体应用。 1. Merkle 算法的原理 …...

【umi max】关于umi构建的项目在本地服务运行正常,但是部署时无致命报错却白屏,html文档的#root容器没有子元素的原因及解决办法
我们在部署时运维很可能会因为项目太多,进而放到不同的目录底下,例如project/H5-TEST-DEMO (其中project是项目的存放目录,而H5-TEST-DEMO才是我们部署的项目根目录)于是乎就会出现我们在本地服务里调试得好好的&#…...

Openlayers高级交互(14/20):汽车移动轨迹动画(开始、暂停、结束)
本示例演示在vue+openlayers中实现轨迹动画,这里设置了小汽车开始,暂停,结束等的控制键,采用了线段步长位置获取坐标来定位点的方式来显示小车的动态。 效果图 专栏名称内容介绍Openlayers基础实战 (72篇)专栏提供73篇文章,为小白群体提供基础知识及示例演示,能解决基…...

蓝牙MCU蓝牙医疗检测相关案例
英尚蓝牙MCU配套成熟的网络协议栈和丰富的示例代码及多平台APP工具。无需二次开发,即连即用;提供特色蓝牙/串口/USB三通芯片,为更多复杂无线应用赋能。相关产品及技术欢迎咨询。 应用案例说明: • 应用包括血糖仪,血氧仪,血压计,体温计,毒品…...

pytorch环境安装和更新,额外装cuda有什么意义
更新了一下设备和环境,看了眼其他教程,突然间发现都还让装cuda和cudnn。。。明明很早之前pytorch使用的和系统的cuda就已经脱钩了。 测试了一下不额外装也没发现什么问题,如果有谁知道装系统的cuda对pytorch有何意义,可以评论区告…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...
