Leetcode 热题100之二叉树2
1.二叉树的层序遍历

思路分析:层序遍历是逐层从左到右访问二叉树的所有节点,通常可以使用广度优先搜索(BFS)来实现。我们可以使用一个队列(FIFO)来存储每一层的节点,并逐层访问。
- 初始化队列:将根节点放入队列中。如果根节点为空,则返回空结果;
- 层级遍历:当队列不为空时,表示还有节点需要访问,每次处理一层
- 获取当前层的节点数量‘
- 遍历当前层的所有节点,将节点值存入结果列表;
- 将当前节点的左右节点加入队列,供下一层使用;
- 返回结果:将每一层的节点值依次存入结果列表并返回。
具体实现代码(详解版):
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> result;//存储层序遍历结果if(root == nullptr) return result;//空树queue<TreeNode*> q;//队列用于广度优先搜索q.push(root);while(!q.empty()){int levelSize = q.size();//当前层的节点梳理vector<int> currentLevel;//存储当前层的节点值for(int i = 0 ; i < levelSize ; i ++){TreeNode* node = q.front();//取出队首节点q.pop();//移除队首节点currentLevel.push_back(node->val);//添加当前节点的值道当前层//将左右子节点加入队列,供下一层访问if(node->left) q.push(node->left);if(node->right) q.push(node->right);}result.push_back(currentLevel);//将当前层加入结果}return result;}
};
- 时间复杂度:O(n),其中n是节点总数。每个节点访问一次
- 空间复杂度:O(n),队列在最坏情况下可能会存储所有叶节点。
2.将有序数组转化为二叉搜索树

思路分析:将一个已排序的整数数组转换为平衡的二叉搜索树(BST)可以通过递归的方法完成。这个问题的关键在于,平衡的二叉搜索树要求左右子树的高度差不超过 1,这可以通过将数组的中间元素作为根节点来实现,左半部分构成左子树,右半部分构成右子树。这样递归下去,可以构造出一个平衡的 BST。
- 选择中间元素:为了让树平衡,应该选择数组的中间元素作为根节点;
- 递归构建左右子树:将左半部分的数组递归构建左子树,右半部分的数组递归构建为右子树。
- 终止条件:当子数组为空时,返回nullptr。
具体实现代码(详解版):
// 辅助函数:递归构建平衡二叉搜索树
TreeNode* buildBST(const vector<int>& nums, int left, int right) {// 终止条件:当左边界超过右边界时,返回空指针if (left > right) return nullptr;// 选择中间元素作为根节点int mid = left + (right - left) / 2;TreeNode* root = new TreeNode(nums[mid]);// 递归构建左子树root->left = buildBST(nums, left, mid - 1);// 递归构建右子树root->right = buildBST(nums, mid + 1, right);// 返回当前子树的根节点return root;
}// 主函数:将排序数组转换为平衡二叉搜索树
TreeNode* sortedArrayToBST(vector<int>& nums) {return buildBST(nums, 0, nums.size() - 1);
}
- 时间复杂度:O(n),其在n是数组的长度。每个元素仅访问一次,用于构建树节点;
- 空间复杂度:O(log n),因为递归深度与树的高度相干。对于平衡的二叉树,高度约为log(n)。
3.验证二叉搜索树

思路分析:
要判断一个二叉树是否是有效的二叉搜索树(BST),可以利用 BST 的性质:
- 左子树的所有节点值必须小于当前节点的值。
- 右子树的所有节点值必须大于当前节点的值。
我们可以通过递归来检查每个节点是否满足这个条件。在递归过程中,为每个节点维护一个允许的值范围(最小值和最大值)。对于当前节点:
- 左子节点的值应该小于当前节点的值,且在当前的最小值到当前节点值的范围内。
- 右子节点的值应该大于当前节点的值,且在当前节点值到当前的最大值范围内。
实现思路:
- 递归检查节点范围:在递归中为每一个节点维护一个值范围;
- 检查左右子树:在每次递归时,左子树的最大值更新为当前节点的值,右子树的最小住更新为当前节点的值;
- 终止条件:如果节点为空,返回true;如果节点值不在指定的范围内,返回false;
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool isValidBST(TreeNode* node , long long minVal , long long maxVal){if(node == nullptr) return true;//检查当前节点是否在允许的范围内if(node->val <= minVal || node->val >= maxVal) return false;//递归检测左子树和右子树//左子树的最大值更新为当前节点的值//右子树的最小值更新为当前节点的值return isValidBST(node->left,minVal,node->val)&& isValidBST(node->right,node->val,maxVal);}bool isValidBST(TreeNode* root) {return isValidBST(root,LONG_LONG_MIN,LONG_LONG_MAX);}
};
- 时间复杂度:O(n),其中n是节点总数,每个节点访问一次;
- 空间复杂度:O(h),其在h是树的高度。
4.二叉搜索树中第k小的元素

思路分析:在二叉搜索树(BST)中,第 k 小的元素可以通过 中序遍历获得,因为中序遍历的结果是按升序排列的。在中序遍历中,只需计数到第 k 个节点即可找到所需的元素。
- 中序遍历:由于二叉搜索树的性质,中序遍历(左根右)会以升序遍历节点;
- 计数节点:在中序遍历时,每访问一个节点,增加计数器。当计数器等于k时,当前节点即为第k小的节点
- 剪枝:当找到第k小的节点后,可以停止遍历,节省不必要的运算。
具体实现代码(详解版):
class Solution {
public:int result = 0;//存储结果int count = 0;//计数器//中序遍历void inorder(TreeNode* node,int k){if(node == nullptr) return;//遍历左子树inorder(node->left,k);//访问当前节点count ++;if(count == k){result = node->val;return;}//遍历右子树inorder(node->right,k);}int kthSmallest(TreeNode* root, int k) {inorder(root,k);return result;}
};
- 时间复杂度:O(h+k),其中h是树的高度,最坏情况下需要遍历k个节点;
- 空间复杂度:O(h),递归调用栈的最大深度和树的高度成正比。
5.二叉树的右视图

思路分析:要从二叉树的右侧查看节点值,可以使用 层序遍历,即逐层遍历二叉树。对于每一层的最右侧节点,将其加入结果列表。我们可以通过 广度优先搜索(BFS) 来实现该过程,因为 BFS 可以方便地按层处理节点。
- 层序遍历:使用队列进行广度优先搜索,从根节点开始按层遍历树;
- 记录每层的最右节点:在遍历每一层的节点时,最后一个访问的节点即为该层的最右侧接待你,将其添加到结果中;
- 继续下一层:继续处理下一层,知道所有节点都被遍历完。
具体实现代码(详解版):
class Solution {
public:vector<int> rightSideView(TreeNode* root) {vector<int> result; // 存储右视图的结果if (root == nullptr) return result; // 如果根节点为空,返回空的结果queue<TreeNode*> q; // 创建一个队列,用于层序遍历二叉树q.push(root); // 将根节点加入队列,开始层序遍历// 循环,直到队列为空while (!q.empty()) {int levelSize = q.size(); // 当前层的节点数TreeNode* currentNode;// 遍历当前层的所有节点for (int i = 0; i < levelSize; ++i) {currentNode = q.front(); // 获取队首节点q.pop(); // 弹出队首节点// 如果存在左子节点,则将其加入队列if (currentNode->left) q.push(currentNode->left);// 如果存在右子节点,则将其加入队列if (currentNode->right) q.push(currentNode->right);}// 当前层的最后一个节点是从右侧可以看到的节点,将其值加入结果result.push_back(currentNode->val);}return result; // 返回右视图的结果}
};- 时间复杂度:O(n),其中n是二叉树的节点数,每个节点都被访问一次;
- 空间复杂度:O(d),其中d是二叉树的最大宽度。
相关文章:

Leetcode 热题100之二叉树2
1.二叉树的层序遍历 思路分析:层序遍历是逐层从左到右访问二叉树的所有节点,通常可以使用广度优先搜索(BFS)来实现。我们可以使用一个队列(FIFO)来存储每一层的节点,并逐层访问。 初始化队列&a…...

<项目代码>YOLOv8 煤矸石识别<目标检测>
YOLOv8是一种单阶段(one-stage)检测算法,它将目标检测问题转化为一个回归问题,能够在一次前向传播过程中同时完成目标的分类和定位任务。相较于两阶段检测算法(如Faster R-CNN),YOLOv8具有更高的…...

GA/T1400视图库平台EasyCVR视频分析设备平台微信H5小程序:智能视频监控的新篇章
GA/T1400视图库平台EasyCVR是一款综合性的视频管理工具,它兼容Windows、Linux(包括CentOS和Ubuntu)以及国产操作系统。这个平台不仅能够接入多种协议,还能将不同格式的视频数据统一转换为标准化的视频流,通过无需插件的…...

LVM与磁盘配额
文章目录 LVM与磁盘配额1 LVM概述1.1 名词解释1.2 LVM优势 2 LVM相关命令2.1 创建逻辑卷过程2.2 对逻辑卷扩容 3 磁盘配额3.1 磁盘配额的特点3.2 磁盘配额的命令3.3 查看配额使用情况3.4 验证磁盘配额3.5 实验 LVM与磁盘配额 1 LVM概述 1.1 名词解释 LVM:logical…...

xmuoj [蒙德里安的梦想] 状压dp个人笔记
本题是状压dp经典题目,很多人都是通过这一题开始对状压dp有所了解。 在进行讲解之前,我们先通过几个问答大致了解状压dp。 一、问答 1. 问题:什么是状压dp? 回答:状压dp即为状态压缩动态规划,何为状态压缩&#x…...

ubuntu22安装搜狗输入法不能输入中文
关闭Wayland 在/etc/gdm3/custom.conf文件内,取消注释WaylandEnable cat /etc/gdm3/custom.conf | grep WaylandEnable WaylandEnablefalse 其它步骤参考搜狗官方教程 https://pinyin.sogou.com/linux/help.php...

HtmlAgilityPack 操作详解
目录 1.安装 HtmlAgilityPack 2. 示例 HTML 3. 使用 HtmlAgilityPack 进行 HTML 解析与操作 4. 代码详解 1.加载html文档 2.选择元素 3. 提取属性 4.修改属性 5.常用的几种获取元素的 XPath 写法 HtmlAgilityPack: 轻量且高效,适合进行常规的 H…...

基于SSM医院门诊互联电子病历管理系统的设计
管理员账户功能包括:系统首页,个人中心,用户管理,医生管理,项目分类管理,项目信息管理,预约信息管理,检查信息管理,系统管理 用户账号功能包括:系统首页&…...
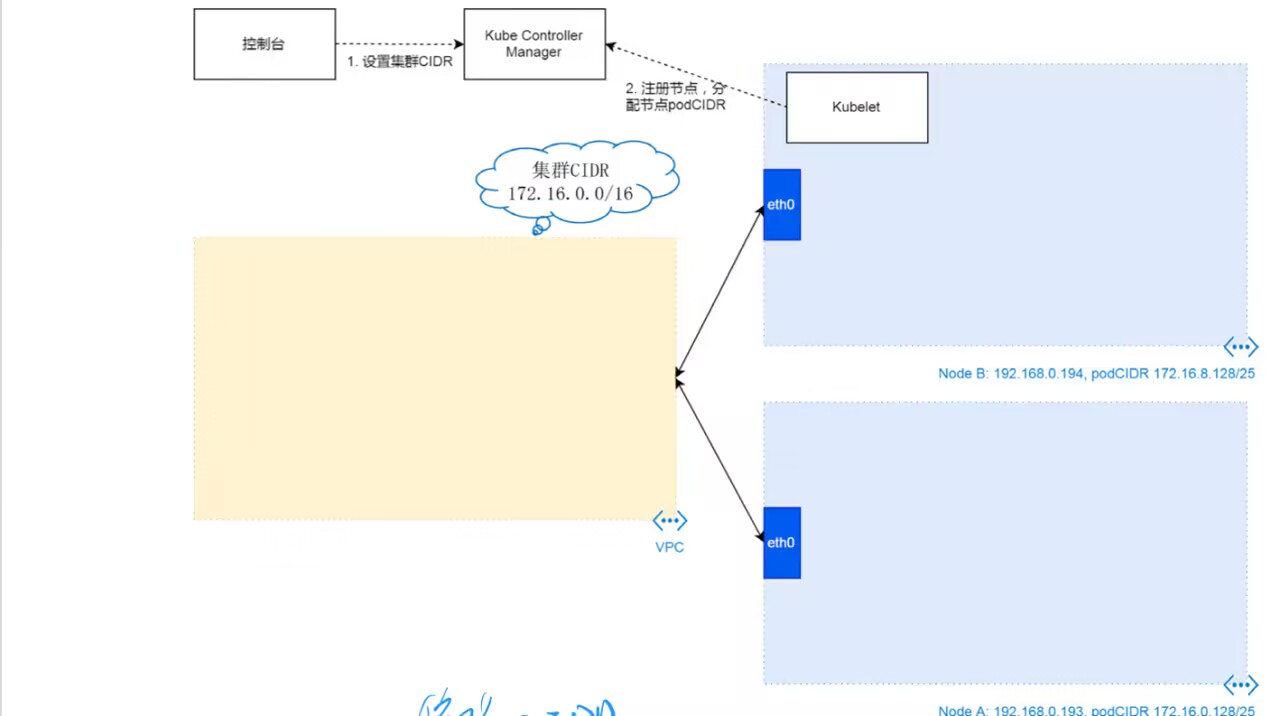
【读书笔记/深入理解K8S】集群网络
前言 上一章讲了集群控制器的一个大概的原理,这一章讲一下集群网络。网络是集群通信的载体,因为该书是阿里云团队出品的,所以也以阿里云的集群网络方案为例,其他云厂商的网络集群方案一般来说也大同小异。所以通过本章的学习&…...
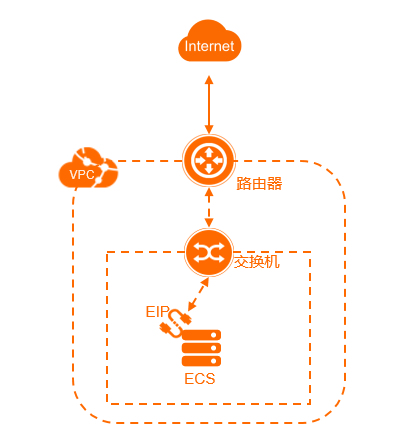
【专有网络VPC】连接公网
通过ECS实例固定公网IP、弹性公网IP、NAT网关、负载均衡使专有网络中的云资源可以访问公网(Internet)或被公网访问。 概述 专有网络是您自定义的云上私有网络。专有网络中的云资源默认无法访问公网,也无法被公网访问。您可以通过配置ECS实例…...

论文 | Legal Prompt Engineering for Multilingual Legal Judgement Prediction
这篇文章探讨了如何利用“法律提示工程”(LPE)来指导大型语言模型(LLM)进行多语言法律判决预测(LJP)。主要内容: LPE 的概念: LPE 是指通过设计特定的提示(promp…...

国科安芯抗辐照MCU和CANFD芯片发布
国科安芯科技有限公司近期发布了两款重要的芯片产品:抗辐照MCU芯片和抗辐照CANFD芯片。这两款芯片的发布标志着国科安芯在高性能、高安全性芯片产品研制方面取得了显著进展,特别是在抗辐照技术领域。 1. 抗辐照MCU芯片:国科安芯研发的AS32A4…...
)
C++ 并发专题 - 无锁数据结构(概述)
一:概述: 无锁数据结构是一种在多线程环境中实现线程安全的结构,它允许多个线程在没有传统锁机制的情况下并发访问和修改数据。这种设计的目标是提高程序的性能和响应性,避免锁竞争和上下文切换的开销。 二:原理&…...

NLP领域的经典算法和模型
在自然语言处理(NLP)领域,经典算法和模型众多,它们在不同任务中发挥着重要作用。以下是一些NLP领域的经典算法和模型的详细介绍: 一、基础模型 词袋模型(Bag of Words,BoW) 原理&a…...

提升安全上网体验:Windows 11 启用 DOH(阿里公共DNS)
文章目录 阿里公共 DNS 介绍免费开通云解析 DNS 服务Windows 编辑 DNS 设置配置 IPv4配置 IPv6 路由器配置 DNS 阿里公共 DNS 介绍 https://alidns.com/ 免费开通云解析 DNS 服务 https://dnsnext.console.aliyun.com/pubDNS 开通服务后,获取 DOH 模板࿰…...

论文概览 |《Journal of Transport Geography》2024.10 Vol.120
本次给大家整理的是《Journal of Transport Geography》杂志2024年9月第120卷的论文的题目和摘要,一共包括17篇SCI论文! 论文1 Modelling scenarios in planning for future employment growth in Stockholm 斯德哥尔摩未来就业增长规划情景建模 【摘要…...

yum不能使用: cannot find a valid baseurl for repo: base/7/x86_64
使用yum命令时报错: 原因: CentOS 已经停止维护的问题。2020 年 12 月 8 号,CentOS 官方宣布了停止维护 CentOS Linux 的计划,并推出了 CentOS Stream 项目,CentOS Linux 8 作为 RHEL 8 的复刻版本,生命周期…...

什么品牌的护眼台灯比较好?五款护眼效果比较明显的护眼台灯
在当今信息爆炸的时代背景下,挑选一款真正符合个人需求的护眼台灯,确实是一项不小的挑战。市场上品牌众多、型号繁杂,功能特点各不相同,价格区间也相当广泛,许多消费者在选购时往往感到迷茫不已。当大家询问“什么品牌…...

HTML 表单设计与验证
创建 HTML 表单的步骤如下: 使用 <form> 标签来创建表单,<form> 标签有一个 action 属性,用于指定表单提交的目标 URL。 在 <form> 标签内部,使用 <input> 标签来创建输入框。<input> 标签有一个 …...

qt QDialog详解
1、概述 QDialog是Qt框架中用于创建对话框的类,它继承自QWidget。QDialog提供了一个模态或非模态的对话框,用于与用户进行交互。模态对话框会阻塞其他窗口的输入,直到用户关闭该对话框;而非模态对话框则允许用户同时与多个窗口进…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
