C++ [项目] 躺平发育
一、基本介绍
支持Dev-C++5.11版本(务必调为英文输入法),基本操作看游戏里的介绍,怎么做的……懒得说,能看懂就看注释,没有的自己猜,如果你很固执……私我吧
二、代码部分
#include<bits/stdc++.h>
#include<windows.h>
#include<unistd.h>
using namespace std;
void rules();
int main() {int c=1;int m=1;long long m_x=1000;long long m_xl=1000;int g_a=250;int g_d=200;int coins=50;int p_n=1;int n=0;int win=100;int buy;int d_n=0;int p_a=75;int p_na, jj_a, jj_d;system("cls");cout<<"请选择难度:"<<endl;cout<<endl;cout<<endl;cout<<"A.初级难度"<<endl;cout<<endl;cout<<"B.中级难度"<<endl;cout<<endl;cout<<"C.地狱难度"<<endl;cout<<"请输入:";char x;cin>>x;if(x=='A'){jj_a=100;jj_d=60;p_na=50;} else if(x=='B'){jj_a=125;jj_d=75;p_na=55;}else if(x=='C'){jj_a=175;jj_d=125;p_na=45;}while(win>=0) {if(n<0){n=0;}if(win<=0){break;}m_xl-=n*g_a;if(m_xl<=0) {system("cls");cout<<"您的门已经被噬梦者攻破,G A M E O V E R!"<<endl;return 0;}system("cls");cout<<"金币:"<<coins<<" 电力:"<<d_n<<" 炮台:"<<p_n<<"个 "<<"门的血量:"<<m_xl<<endl;cout<<endl;cout<<" 墙墙墙墙 墙墙墙墙"<<endl;cout<<" 墙◎◎墙 墙◎◎墙"<<endl;cout<<" 墙◎◎墙 墙◎◎墙"<<endl;cout<<" 墙◎◎墙 墙◎◎墙"<<endl;cout<<" 墙 墙 墙 墙"<<endl;cout<<" 墙 墙 怪 墙 墙"<<endl;cout<<" 墙 墙 "<<n<<"墙 墙"<<endl;cout<<"墙墙墙墙 墙 门 墙 墙墙墙墙"<<endl;cout<<"墙 ◎◎ ◎ 墙"<<endl;cout<<"墙 ◎床◎ ☆☆☆墙"<<endl;cout<<"墙 ☆★★墙"<<endl;cout<<"墙 ☆★★墙"<<endl;cout<<"墙墙墙墙墙墙墙墙墙墙墙墙墙墙墙墙"<<endl;cout<<endl;cout<<"您正在床上发育……"<<endl;cout<<"有"<<n<<"只噬梦者在挠你的门!"<<endl;cout<<"输入1以建造炮台:25金币"<<endl;cout<<"输入2以升级门: 50金币"<<endl;cout<<"输入3以升级床: 35金币"<<endl;cout<<"输入4以放弃此次建造机会"<<endl;cout<<"输入5以拆除1个炮台:获得15金币"<<endl;cout<<"输入6以让门回血"<<endl;cout<<"您的门的级位是"<<m<<"级"<<endl;cout<<"您的床是"<<c<<"级"<<endl;cout<<"◎:炮台"<<endl;cout<<"☆:维修台"<<endl;cout<<"★:发电机"<<endl;n-=p_n*p_a/g_d;win-=p_n*p_a/g_d;cin>>buy;switch(buy) {case 1:if(coins<25) {cout<<"您的钱不够"<<endl;break;}if(p_n==17){cout<<"最大上限为17个炮台!"<<endl;break;} coins-=25;p_n++;break;case 2:if(coins<50) {cout<<"您的钱不够"<<endl;break;}if(m==19){cout<<"您的门已达到黄金门,不能够再次升级了!"<<endl;system("pause");break;}coins-=50;m++;m_x*=7;m_xl=m_x;break;case 3:if(coins<35) {cout<<"您的钱不够"<<endl;break;}coins-=35;c++;break;case 4:break;case 5:coins+=15;p_n--;case 6:m_xl=m_x;break;default:cout<<"没有此选项"<<endl;break;}if(m_xl==0) {system("cls");cout<<"您的门已经被噬梦者攻破,G A M E O V E R!"<<endl;return 0;}if(n==31) {n--;}coins+=c*15;sleep(2);n++;if(n==31) {n--;}d_n+=4*10000;}cout<<"恭喜您打败了所有噬梦者,获得了胜利!"<<endl;
}
void rules() {string o="您在野外建造了一间房屋,现在是晚上,有噬梦者来攻击您。如果您能打败所有(100个)噬梦者,您就胜利了!如果门被挠破,则输!";for(int i=0; i<o.size(); i++) {cout<<o[i];Sleep(100);}cout<<endl;cout<<endl;system("pause");
}如果觉得不错就点个赞吧
相关文章:

C++ [项目] 躺平发育
一、基本介绍 支持Dev-C5.11版本(务必调为英文输入法),基本操作看游戏里的介绍,怎么做的……懒得说,能看懂就看注释,没有的自己猜,如果你很固执……私我吧 二、代码部分 #include<bits/stdc.h> #include<windows.h> #include<unistd.h> using namespace st…...

[产品管理-55]:产品设计不仅仅完成功能,即可用性设计,还需要完成可生产性、可装配性、可维护性、可回收性、可服务性设计
目录 可用性设计: 可生产性设计: 可装配性设计: 可维护性设计: 可回收性设计: 可服务性设计: 产品设计是一个综合性的过程,它不仅仅局限于完成产品的基本功能,即可用性设计&am…...

Mount Image Pro,在取证安全的环境中挂载和访问镜像文件内容
天津鸿萌科贸发展有限公司从事数据安全服务二十余年,致力于为各领域客户提供专业的数据恢复、数据备份解决方案与服务,并针对企业面临的数据安全风险,提供专业的相关数据安全培训。 天津鸿萌科贸发展有限公司是 GetData 公司数据恢复与取证工…...

玩转Docker | Docker基础入门与常用命令指南
玩转Docker | Docker基础入门与常用命令指南 引言基本概念help帮助信息常用命令管理镜像运行容器构建镜像其他Docker命令整理结语引言 Docker 是一种开源的应用容器引擎,它允许开发者将应用程序及其依赖打包进一个可移植的容器中,然后发布到任何流行的 Linux 机器上。这大大简…...

【MySQL】MySQL安装以及各种报错处理
前言: 本节内容讲述在Ubuntu环境下怎么进行MySQL的安装。 以及一些安装过程中遇到的报错如何处理的问题。 ps:注意, 本篇文章不是图形化界面的MySQL安装教程哦。想要安装图形化界面的MySQL的友友们可以另寻资源了。 目录 更新软件包列表 安装M…...

【传知代码】图像处理解决种子计数方法
文章目录 一、背景及意义介绍研究背景农业考种需求传统计数方法的局限性人工计数仪器设备计数 研究意义提高育种效率提高计数准确性广泛的适用性数据存档与分析便利 二、概述三、材料与数据准备以及方法介绍整体流程图像采集图像预处理形态学操作腐蚀运算开运算 图像二值化种子…...

WPF 特性------Binding
工业控制中,经常会需要把一个bool 型输入信号的状态显示在面板上,使用wpf 绑定的办法,可简洁实现: 实现步骤: 1,定义类: using System; using System.Collections.Generic; using System.Com…...

深入解析 FastAPI 查询参数:配置、类型转换与灵活组合
深入解析 FastAPI 查询参数:配置、类型转换与灵活组合 本文全面解析了 FastAPI 查询参数的使用方法,包括配置默认值、设为可选或必选参数、类型转换以及组合使用等实用技巧。通过查询参数,开发者可以在路径操作函数中接收动态输入࿰…...

大学城水电管理系统开发:Spring Boot指南
2相关技术 2.1 MYSQL数据库 MySQL是一个真正的多用户、多线程SQL数据库服务器。 是基于SQL的客户/服务器模式的关系数据库管理系统,它的有点有有功能强大、使用简单、管理方便、安全可靠性高、运行速度快、多线程、跨平台性、完全网络化、稳定性等,非常…...

Lua 从基础入门到精通(非常详细)
目录 什么是 Lua? Lua 环境安装 Lua基本语法 注释 数据类型 nil(空) Boolean number(数字) string(字符串) function(函数) userdata thread tableÿ…...

[MySQL#11] 索引底层(2) | B+树 | 索引的CURD | 全文索引
目录 1.B树的特点 索引结构 复盘 其他数据结构的对比 B树与B树总结 聚簇索引与非聚簇索引 辅助索引 2. 索引操作 主键索引 1. 创建主键索引 第一种方式 第二种方式 第三种方式 2. 查询索引 第一种方法 第二种方法 第三种方法 3. 删除索引 删除主键索引 删除…...

一个指针可以被声明为 `volatile`
一个指针可以被声明为 volatile。当指针被声明为 volatile 时,指针本身的地址值可能会在程序之外的控制下发生变化,这意味着编译器在使用该指针时必须每次都重新从内存中读取它的地址,而不能假设指针的地址保持不变。 为什么指针可以是 vola…...

[0260].第25节:锁的不同角度分类
MySQL学习大纲 我的数据库学习大纲 从不同维度对锁的分类: 1.对数据操作的类型划分:读锁和写锁 1.1.读锁 与 写锁概述: 1.对于数据库中并发事务的读-读情况并不会引起什么问题。对于写-写、读-写或写-读这些情况可能会引起一些问题,需要使用…...

android数组控件Textview
说明:android循环控件,注册和显示内容 效果图: step1: E:\projectgood\resget\demozz\IosDialogDemo-main\app\src\main\java\com\example\iosdialogdemo\TimerActivity.java package com.example.iosdialogdemo;import android.os.Bundl…...

openpnp - 手工修改配置文件(元件高度,size,吸嘴)
文章目录 openpnp - 手工修改配置文件(元件高度,size,吸嘴)概述笔记parts.xmlpackages.xml 手工将已经存在的NT1,NT2拷贝出来改名备注END openpnp - 手工修改配置文件(元件高度,size,吸嘴) 概述 载入新板子贴片准备时,除了引入Named CSV文件,还要在ope…...

Java 集合一口气讲完!(中)d=====( ̄▽ ̄*)b
Java 队列 Java集合教程 - Java队列 队列是只能在其上执行操作的对象的集合两端的队列。 队列有两个末端,称为头和尾。 在简单队列中,对象被添加到尾部并从头部删除并首先删除首先添加的对象。 Java Collections Framework支持以下类型的队列。 简单…...

位运算:计算机科学中的基本操作
深入探讨位运算:计算机科学中的基本操作 位运算是计算机科学中的一种重要工具,它直接作用于数据的二进制位,能够高效地进行数据处理。本文将详细介绍位运算的基本概念、种类以及其实际应用。 什么是位运算? 位运算是对整数的二…...

MPSK(BPSK/QPSK/8PSK)调制解调的Matlab仿真全套
一、概述 MPSK(BPSK、QPSK、8PSK)等是常用的相位调制方式,本文对数据获取、比特流组织、基带调制、上变频发送、添加噪声、接收下变频、基带解调、数据还原等过程进行仿真。 模块化、通用化设计,将函数分为(1)数据读取转比特流;(2)基带调制【参数控制调制类型】;(…...
编写程序)
如何为STM32的EXTI(外部中断)编写程序
要为STM32的EXTI(外部中断)编写程序,你需要遵循以下步骤: 1. 初始化GPIO 首先,需要初始化连接到外部中断线的GPIO引脚。这个引脚需要配置为输入模式,并且根据需要选择上拉、下拉或浮空。 GPIO_InitTypeDe…...
八、快速入门Kubernetes之service
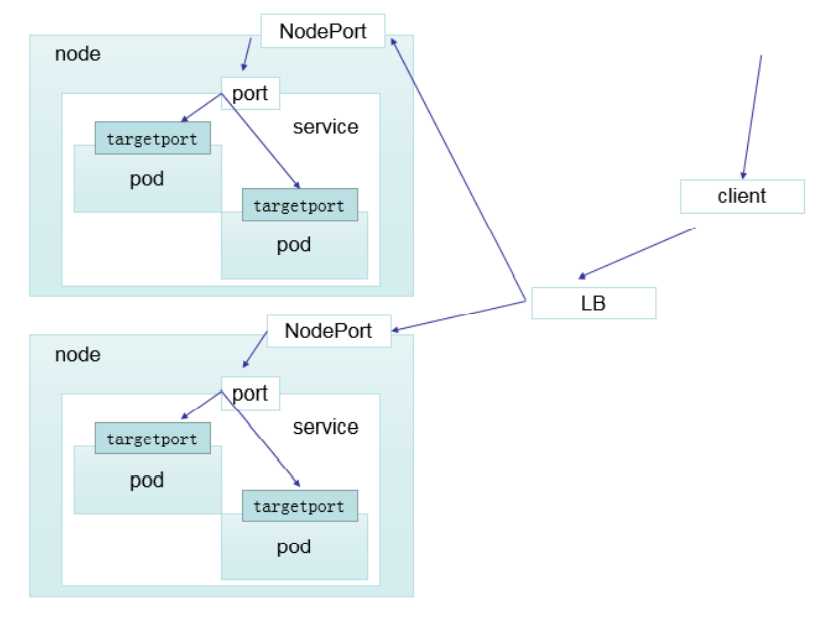
文章目录 Service:one: VIP和Service代理:star: 代理模式分类2、iptables代理模式3、ipvs代理模式 :two: ClusterIP:three:实列Service:four: Headless Service实列:five: NodePort:six: LoadBalancer:seven: ExternalName Service ⭐️ 概念:Kubernetes Service 定…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

React父子组件通信:Props怎么用?如何从父组件向子组件传递数据?
系列回顾: 在上一篇《React核心概念:State是什么?》中,我们学习了如何使用useState让一个组件拥有自己的内部数据(State),并通过一个计数器案例,实现了组件的自我更新。这很棒&#…...

Win系统权限提升篇UAC绕过DLL劫持未引号路径可控服务全检项目
应用场景: 1、常规某个机器被钓鱼后门攻击后,我们需要做更高权限操作或权限维持等。 2、内网域中某个机器被钓鱼后门攻击后,我们需要对后续内网域做安全测试。 #Win10&11-BypassUAC自动提权-MSF&UACME 为了远程执行目标的exe或者b…...

Android Framework预装traceroute执行文件到system/bin下
文章目录 Android SDK中寻找traceroute代码内置traceroute到SDK中traceroute参数说明-I 参数(使用 ICMP Echo 请求)-T 参数(使用 TCP SYN 包) 相关文章 Android SDK中寻找traceroute代码 设备使用的是Android 11,在/s…...
