《GBDT 算法的原理推导》 11-12计算损失函数的负梯度 公式解析
本文是将文章《GBDT 算法的原理推导》中的公式单独拿出来做一个详细的解析,便于初学者更好的理解。
公式(11-12)是GBDT算法中非常关键的一步,它表示了如何通过计算损失函数的负梯度来指导下一棵树的生长。
公式(11-12)如下:
r m i = − [ ∂ L ( y i , f ( x i ) ) ∂ f ( x i ) ] f ( x ) = f m − 1 ( x ) r_{mi} = - \left[ \frac{\partial L(y_i, f(x_i))}{\partial f(x_i)} \right]_{f(x) = f_{m-1}(x)} rmi=−[∂f(xi)∂L(yi,f(xi))]f(x)=fm−1(x)
1. 公式的背景
在GBDT中,我们的目标是最小化一个损失函数 L ( y , f ( x ) ) L(y, f(x)) L(y,f(x)),其中:
- y y y 是真实值,
- f ( x ) f(x) f(x) 是模型的预测值。
每一轮 m m m 的模型 f m ( x ) f_m(x) fm(x) 是在前一轮的基础上进行改进的,即:
f m ( x ) = f m − 1 ( x ) + T ( x ; Θ m ) f_m(x) = f_{m-1}(x) + T(x; \Theta_m) fm(x)=fm−1(x)+T(x;Θm)
这里的 T ( x ; Θ m ) T(x; \Theta_m) T(x;Θm) 是新增的树,我们希望它能纠正前一轮模型 f m − 1 ( x ) f_{m-1}(x) fm−1(x) 的误差。
2. 负梯度的意义
为了指导新树的构建,我们需要让新树 T ( x ; Θ m ) T(x; \Theta_m) T(x;Θm) 能够减少当前模型 f m − 1 ( x ) f_{m-1}(x) fm−1(x) 的误差。GBDT使用了一个关键的技巧:用损失函数的负梯度来近似每个样本的残差,即误差。
- 损失函数的负梯度表示模型需要改进的方向。通过沿着负梯度的方向优化,我们可以使得损失逐步减小。
- 具体来说,公式(11-12)中的 r m i r_{mi} rmi 是第 m m m 轮中第 i i i 个样本的负梯度,它表示当前模型对该样本的误差方向和大小。
3. 公式(11-12)的含义
公式(11-12)中的 r m i r_{mi} rmi 是针对第 m m m 轮中第 i i i 个样本计算的负梯度:
r m i = − [ ∂ L ( y i , f ( x i ) ) ∂ f ( x i ) ] f ( x ) = f m − 1 ( x ) r_{mi} = - \left[ \frac{\partial L(y_i, f(x_i))}{\partial f(x_i)} \right]_{f(x) = f_{m-1}(x)} rmi=−[∂f(xi)∂L(yi,f(xi))]f(x)=fm−1(x)
其中:
- L ( y i , f ( x i ) ) L(y_i, f(x_i)) L(yi,f(xi)) 是损失函数,表示模型预测 f ( x i ) f(x_i) f(xi) 与真实值 y i y_i yi 之间的误差。
- ∂ L ( y i , f ( x i ) ) ∂ f ( x i ) \frac{\partial L(y_i, f(x_i))}{\partial f(x_i)} ∂f(xi)∂L(yi,f(xi)) 是损失函数关于模型输出 f ( x i ) f(x_i) f(xi) 的偏导数。偏导数表示的是损失函数在 f ( x i ) f(x_i) f(xi) 处的变化趋势。
- 负号 − - − 表示我们要沿着负梯度方向去优化,即在模型的当前输出基础上减少误差。
因此, r m i r_{mi} rmi 表示的是在第 m m m 轮中,第 i i i 个样本的当前模型预测值与真实值之间的差异(残差)的一个估计,并且这个估计是基于损失函数的梯度计算的。
4. 负梯度用于训练新树
在GBDT的第 m m m 轮中,新树 T ( x ; Θ m ) T(x; \Theta_m) T(x;Θm) 是通过拟合所有样本的负梯度 r m i r_{mi} rmi 来生成的。也就是说,这棵新树的任务是尽可能准确地拟合当前模型的“误差”部分,从而在下一轮更新中进一步减少总损失。
5. 举个例子
假设我们使用的是平方损失函数:
L ( y i , f ( x i ) ) = 1 2 ( y i − f ( x i ) ) 2 L(y_i, f(x_i)) = \frac{1}{2} (y_i - f(x_i))^2 L(yi,f(xi))=21(yi−f(xi))2
那么,损失函数对于 f ( x i ) f(x_i) f(xi) 的导数是:
∂ L ( y i , f ( x i ) ) ∂ f ( x i ) = f ( x i ) − y i \frac{\partial L(y_i, f(x_i))}{\partial f(x_i)} = f(x_i) - y_i ∂f(xi)∂L(yi,f(xi))=f(xi)−yi
因此,在平方损失的情况下,公式(11-12)中的负梯度就是:
r m i = − ( f m − 1 ( x i ) − y i ) = y i − f m − 1 ( x i ) r_{mi} = - (f_{m-1}(x_i) - y_i) = y_i - f_{m-1}(x_i) rmi=−(fm−1(xi)−yi)=yi−fm−1(xi)
这表示负梯度等于当前模型的残差 y i − f m − 1 ( x i ) y_i - f_{m-1}(x_i) yi−fm−1(xi),即真实值和预测值的差值。因此,新的树会拟合这个残差,从而在下一轮更新时使模型预测值更接近真实值。
总结
公式(11-12)表示,GBDT中的每一轮迭代都使用当前模型的损失函数负梯度作为新的目标值,以此指导下一棵树的生成。这种方法使得每一棵新树都在不断纠正前面模型的不足,逐步提升整体模型的性能。
相关文章:

《GBDT 算法的原理推导》 11-12计算损失函数的负梯度 公式解析
本文是将文章《GBDT 算法的原理推导》中的公式单独拿出来做一个详细的解析,便于初学者更好的理解。 公式(11-12)是GBDT算法中非常关键的一步,它表示了如何通过计算损失函数的负梯度来指导下一棵树的生长。 公式(11-12)如下: r m i − [ ∂ …...

mysql设计
大家好,我是捡田螺的小男孩。 昨天一位粉丝,咨询了一个并发的问题~ 我提供了一个乐观锁兜底的方案,然后发现他们的表,都没有加version字段的,我想到,这不是表设计通用字段嘛。因此,本文跟大家聊聊…...

Android 斗鱼面经
Android 斗鱼面经 文章目录 Android 斗鱼面经一面二面 一面 先简单描述一下JVM JRE JDK的关系 :::info JVM(Java Virtual Machine) Java 虚拟机。它只认识 xxx.class 这种类型的文件,它能够将 class 文件中的字节码指令进行识别并调用操作…...

【机器学习】26. 聚类评估方法
聚类评估方法 1. Unsupervised Measure1.1. Method 1: measure cohesion and separationSilhouette coefficient Method 2:Correlation between two similarity matricesMethod 3:Visual Inspection of similarity matrix 2. Supervised measures3. 决定…...

linux 最多能创建多少个 TCP 连接?
linux 最大允许TCP连接数 约束一:服务器的端口范围约束二,服务器文件描述符限制约束三:系统线程约束四:系统内存总结 tcp连接四元组:源ip,源端口 <> 目标ip,目标端口 连续对同一个目标ip及…...

我为何要用wordpress搭建一个自己的独立博客
我在csdn有一个博客,这个博客是之前学习编程时建立的。 博客有哪些好处呢? 1,可以写自己的遇到的问题和如何解决的步骤 2,心得体会,经验,和踩坑 3,可以转载别人的好的技术知识 4,宝贵…...

Linux系统每日定时备份mysql数据
一、创建存储脚本的文件夹 创建文件夹,我的脚本放在/root/dbback/mysql mkdir ... cd /root/dbback/mysql 二、编写脚本 vi backup_mysql.sh 复制脚本内容 DB_USER"填写用户名" DB_PASSWORD"填写密码" DB_NAME"数据库名称" # …...

书生大模型第一关Linux基础知识
任务一:完成SSH连接与端口映射并运行hello_world.py 1.SSH及其端口映射 2.在VSCode中安装插件: 3.创建开发机 最后点击创建,然后可能需要等待一段较长的时间,大概需要5分钟左右,如果需要排队则更长时间 然后选择…...

机器学习之fetch_olivetti_faces人脸识别--基于Python实现
fetch_olivetti_faces 数据集下载 fetch_olivetti_faceshttps://github.com/jikechao/olivettifaces sklearn.datasets.fetch_olivetti_faces(*, data_homeNone, shuffleFalse, random_state0, download_if_missingTrue, return_X_yFalse, n_retries3, delay1.0)[source] L…...

【系统设计】深入理解HTTP缓存机制:从Read-Through缓存到HTTP缓存的交互流程
在现代Web开发中,缓存机制扮演着至关重要的角色。它不仅提升了用户体验,还极大地优化了资源的使用效率。在这篇博文中,我们将从“Read-Through”缓存的概念出发,深入探讨HTTP缓存的工作原理和交互流程,并详细描述max-a…...

FLINK单机版安装部署入门-1
文章目录 FLINK单机版安装部署高于1.9.3需要修改配置文件flink-conf.yaml(低于1.9.3可以跳过)linux启动集群windows下启动Flink实例运行(单机)还有一种方式是上传任务包运行examples\streamingjava: Compilation failed: internal java compiler error高版本启动脚本 FLINK单机…...

深度学习-学习率调整策略
在深度学习中,学习率调整策略(Learning Rate Scheduling)用于在训练过程中动态调整学习率,以实现更快的收敛和更好的模型性能。选择合适的学习率策略可以避免模型陷入局部最优、震荡不稳定等问题。下面介绍一些常见的学习率调整策…...

【学员提问bug】小程序在onUnload里面调接口,用来记录退出的时间, 但是接口调用还没成功, 页面就关闭了。如何让接口在onUnload关闭前调用成功?
这种问题比较通用,并不涉及到具体方法执行障碍,所以,解决起来也不麻烦。但是新手往往不知道如何做。 在小程序中,如果在 onUnload 中调用 API 记录页面退出时间,但因为页面关闭速度较快导致请求未完成,可以…...

【刷题13】链表专题
目录 一、两数相加二、两两交换链表的节点三、重排链表四、合并k个升序链表五、k个一组翻转链表 一、两数相加 题目: 思路: 注意整数是逆序存储的,结果要按照题目的要求用链表连接起来遍历l1的cur1,遍历l2的cur2,和…...

Python Turtle模块详解与使用教程
Python Turtle模块详解与使用教程 引言 Python是一种广泛使用的编程语言,其简洁易读的语法使得它成为初学者学习编程的理想选择。而Turtle模块则是Python标准库中一个非常有趣且实用的图形绘制工具,特别适合用于教育和学习编程的基础知识。通过Turtle模…...

【PTA】4-2 树的同构【数据结构】
给定两棵树 T1 和 T2。如果 T1 可以通过若干次左右孩子互换就变成 T2,则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的,因为我们把其中一棵树的结点A、B、G的左右孩子互换后,就得到另外一棵树。而图2就不是同构的。 图一…...

Node.js——fs模块-同步与异步
本文的分享到此结束,欢迎大家评论区一同讨论学习,下一篇继续分享Node.js的fs模块文件追加写入的学习。...
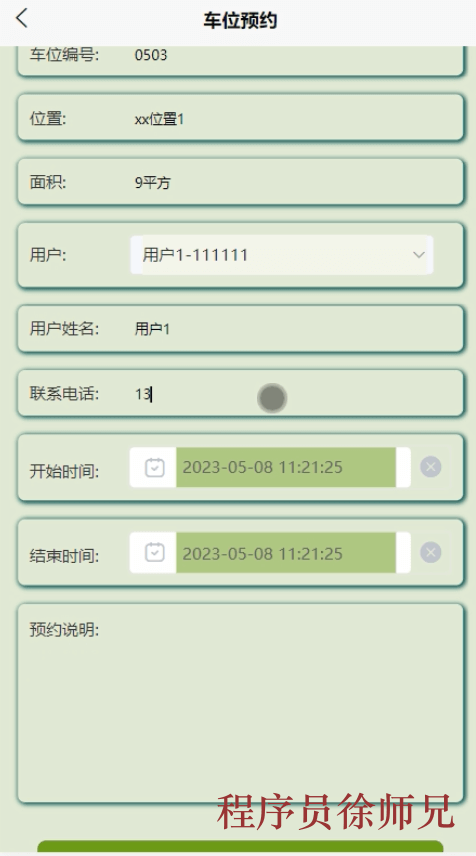
Java基于微信小程序的私家车位共享系统(附源码,文档)
博主介绍:✌stormjun、8年大厂程序员经历。全网粉丝15w、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇&…...
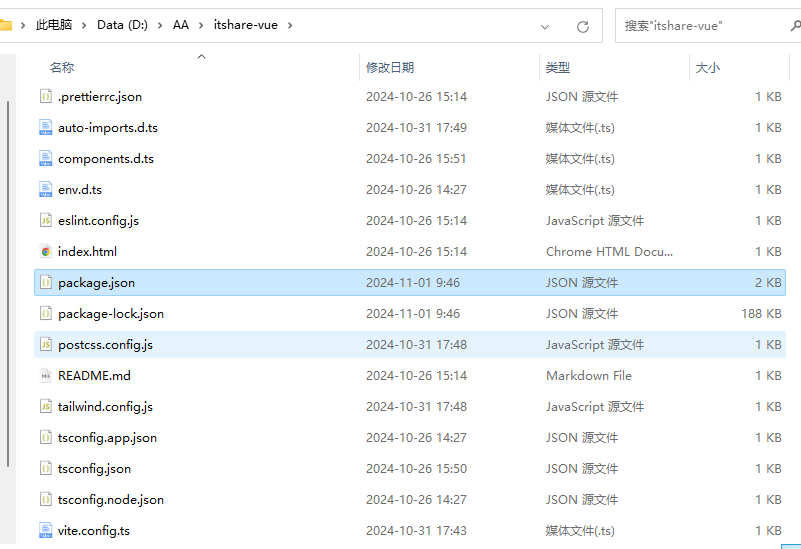
vscode 创建 vue 项目时,配置文件为什么收缩到一起展示了?
一、前言 今天用 vue 官方脚手架创建工程,然后通过 vscode 打开项目发现,配置文件都被收缩在一起了。就像下面这样 这有点反直觉,他们应该是在同一层级下的,怎么会这样,有点好奇,但是打开资源管理查看&…...

PySpark任务提交
一般情况下,spark任务是用scala开发的,但是对于一些偏业务人员,或者是基于上手的来说python的API确实降低了开发前置条件的难度,首当其冲的就是能跳过Java和Scala需要的知识储备,但是在提交任务到集群的时候就很麻烦了…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...
