从0开始学统计-什么是中心极限定理
引言
中心极限定理(Central Limit Theorem, CLT)是统计学中的一块基石,它揭示了一个难以置信的数学现象:无论一个随机变量的原始分布如何,只要我们取足够大的样本量,这些样本的平均值(或总和)的分布将趋近于正态分布,这种分布也被称为高斯分布。中心极限定理不仅为我们使用正态分布进行推断提供了理论基础,还让正态分布成了统计学中最为重要的分布之一。
历史
在统计学史上,中心极限定理的发展是一个渐进的过程。它不是一夜之间形成的,而是经过几个世纪的逐步完善,包含了多个数学家和统计学家的贡献。
18世纪,数学家棣莫弗(Abraham de Moivre)和拉普拉斯(Pierre-Simon Laplace)等开始探索二项分布的性质。1718年,在第一本概率理论书籍《道德和机遇的教训》(“The Doctrine of Chances”)中,棣莫弗首次提出了二项分布在大样本极限下趋近于正态分布的概念,这可以看作是中心极限定理的早期形态。拉普拉斯进一步扩展了这个概念,在1812年的《概率分析理论》(“Théorie Analytique des Probabilités”)中,他通过拉普拉斯展开(Laplace expansion)详细论述了这一点,说明在大数极限下,还有更多的分布趋近于正态分布。
1901年,李雅普诺夫(Aleksandr Lyapunov)证明了一个更一般形式的中心极限定理。该定理不仅适用于二项分布,而且适用于任意有限方差的独立随机变量。李雅普诺夫的工作标志着中心极限定理现代形式的开始。
20世纪中叶,数学家们进一步扩展了中心极限定理的适用范围和形式,其中包括对独立但不同分布的随机变量之和的考虑,以及对随机变量序列弱依赖条件下的应用。
什么是中心极限?
让我们来看一个经典的例子,抛硬币实验。假设我们抛硬币的结果只有两种可能:正面(我们记为1)和反面(我们记为0)。每次抛硬币是一个独立的随机试验,结果的分布是二项分布。
现在,我们进行一系列实验。在每个实验中,我们不止抛一次硬币,而是连续抛硬币n次,并记录正面出现的次数。为了直观展示中心极限定理,我们可以重复进行多个这样的实验(例如,1000次),每次都记录下正面出现的比例。例如,做10个抛10次硬币的实验,在4个左右的实验中,有5次朝上,如图所示:
 根据中心极限定理,不管单次抛硬币的结果分布如何,只要我们重复足够多次抛硬币操作,并且记录下正面出现的比例,这些比例的分布会趋近于正态分布。具体来说,随着实验次数的增加,这些比例的分布会越来越接近于一个均值为μ=0.5、方差为σ2/n(2指平方)的正态分布,其中σ2=0.25是单次抛硬币结果的方差,n是每次实验中抛硬币的次数。
根据中心极限定理,不管单次抛硬币的结果分布如何,只要我们重复足够多次抛硬币操作,并且记录下正面出现的比例,这些比例的分布会趋近于正态分布。具体来说,随着实验次数的增加,这些比例的分布会越来越接近于一个均值为μ=0.5、方差为σ2/n(2指平方)的正态分布,其中σ2=0.25是单次抛硬币结果的方差,n是每次实验中抛硬币的次数。
抛硬币实验说明,即使基础数据(正面或反面)不服从正态分布,大量独立实验的平均结果(或求和结果)也将趋向于正态分布。
什么是期望值?
期望值(Expected Value),也称为数学期望或均值,指在多次随机试验中某个随机变量可能结果的加权平均。对于离散随机变量,期望值是各可能值与其发生概率乘积的总和;对于连续随机变量,期望值是随机变量的概率密度函数乘以随机变量值的积分。
举个例子,假设你有一个标准的六面骰子,每面上的数字分别是1到6。这个实验的随机变量X就是骰子显示的面的数字。因为骰子是公平的,所以每个数字出现的概率都是相同的,即1/6。
我们想计算这个随机变量的期望值,也就是你在多次的掷骰子实验中,可以期待的平均骰子点数。期望值E(X)的计算公式是:

其中xi是第i面的数字,P(X=xi)是该面出现的概率。因此,对于六面骰子,期望值计算如下:

这意味着,虽然你不可能真的掷出3.5(因为骰子的面上没有3.5),但如果你做了很多次实验,那么平均每次掷出的期望是3.5。换句话说,期望值给出了在大量重复实验中,观察到的平均结果。
期望值是理论上的平均值。在实际的骰子游戏中,你每次掷骰子的结果是1到6中的一个整数,但如果你记录下非常多次掷骰子的结果,计算平均值,这个平均值会接近于3.5,这就是期望值的含义。
什么是二项分布?
二项分布( binomial distribution)是一种离散概率分布,它描述了在一系列独立的是/非(成功/失败)实验中,获得固定数量成功次数的概率。在独立的是/非(成功/失败)多次实验中,每次实验都被称为伯努利试验,它只有两种可能的结果:成功或失败。二项分布的典型特征是每次试验的成功概率不变。
让我们来看一个具体的例子,一个篮球运动员进行自由投篮训练。假设一个篮球运动员进行10次自由投篮,每次投篮成功的概率是0.5(即50%)。我们想要知道这个运动员在10次投篮中恰好投中5次的概率是多少。这个实验是一个典型的二项分布情景,因为:每次投篮(试验)只有两种可能结果:成功(投中)或失败(未投中)。每次投篮是独立的,即每次投篮的成功概率保持不变,不受前一次投篮结果的影响。我们关注的是在固定次数(n=10次投篮)的试验中成功的次数。使用二项分布的计算公式:
 代入数值:
代入数值:

其中,0.5是5次成功的概率,(1-0.5)的5次方部分是剩下的5次试验中失败的概率。计算结果为24.6%。因此,这位篮球运动员在10次自由投篮中恰好投中5次的概率大约是24.6%。
小结
中心极限定理的发展历程凝聚了多位数学家和统计学家的智慧。今天,中心极限定理不仅在统计学中占据着中心地位,也在社会科学、自然科学乃至于质量控制和金融工程等应用领域发挥着至关重要的作用。
相关文章:

从0开始学统计-什么是中心极限定理
引言 中心极限定理(Central Limit Theorem, CLT)是统计学中的一块基石,它揭示了一个难以置信的数学现象:无论一个随机变量的原始分布如何,只要我们取足够大的样本量,这些样本的平均值(或总和&a…...

工具方法 - 个人活动的分类
人类活动的分类是一个复杂的话题,因为人类的活动范围非常广泛且相互交叉。然而,我们可以尝试将人类的活动大致分为以下几个主要类别: 工作活动 工作活动是人类生活中不可或缺的一部分,通常包括以下方面: 1. 职业工作&a…...

11.1组会汇报-基于区块链的安全多方计算研究现状与展望
基础知识 *1.背书,这个词源来自银行票据业务,是指票据转让时,原持有人在票据背面加盖自己的印鉴,证明该票据真实有效、如果有问题就可以找原持有人。 区块链中的背书就好理解了。可以简单的理解为验证交易并声明此交易合法&…...

ubuntu【桌面】 配置NAT模式固定IP
DHCP分配导致虚拟机IP老变,SSH老要重新配置,设成静态方便些 一、设NAT模式 1、设为NAT模式 2、看模式对应的虚拟网卡 - VMnet8 3、共享主机网卡网络到虚拟网卡 - VMnet8 二、为虚拟网卡设置静态IP 记住这个IP 三、设置ubuntu固定IP 1、关闭DHCP并…...

评估 机器学习 回归模型 的性能和准确度
回归 是一种常用的预测模型,用于预测一个连续因变量和一个或多个自变量之间的关系。 那么,最后评估 回归模型 的性能和准确度非常重要,可以帮助我们判断模型是否有效并进行改进。 接下来,和大家分享如何评估 回归模型 的性能和准…...

如何下载安装TestLink?
一、下载TestLink、XAMPP TestLink 下载 |SourceForge.net 备用:GitHub - TestLinkOpenSourceTRMS/testlink-code: TestLink开源测试和需求管理系统 下载XAMPP: Download XAMPP 注意:TestLink与PHP版本有关系,所以XA…...

基于SSM+微信小程序的订餐管理系统(点餐2)
👉文末查看项目功能视频演示获取源码sql脚本视频导入教程视频 1、项目介绍 基于SSM微信小程序的订餐管理系统实现了管理员和用户。管理端实现了 首页、个人中心、用户管理、菜品分类管理、菜品信息管理、订单信息管理、配送信息管理、菜品评价管理、订单投诉管理、…...

【C++排序 双指针】1996. 游戏中弱角色的数量|1996
本文涉及的基础知识点 排序 C算法:滑动窗口及双指针总结 本题其它解法 【C单调栈 排序】1996. 游戏中弱角色的数量|1996 LeetCode1996. 游戏中弱角色的数量 你正在参加一个多角色游戏,每个角色都有两个主要属性:攻击 和 防御 。给你一个…...

GESP4级考试语法知识(捕捉异常)
参考程序代码: #include <iostream> using namespace std;double divide(double a, double b) {if (b 0) {throw "Division by zero error"; // 抛出异常}return a / b; }int main() {double num1, num2;cout << "Enter two numbers:…...

HTML 基础标签——元数据标签 <meta>
文章目录 1. `<meta>` 标签概述2. 属性详解2.1 `charset` 属性2.2 `name` 属性2.3 `content` 属性2.4 `http-equiv` 属性3. 其他常见属性小结在 HTML 文档中,元数据标签 <meta> 是一种重要的标签,用于提供关于文档的信息,这些信息不直接显示在网页内容中,但对于…...
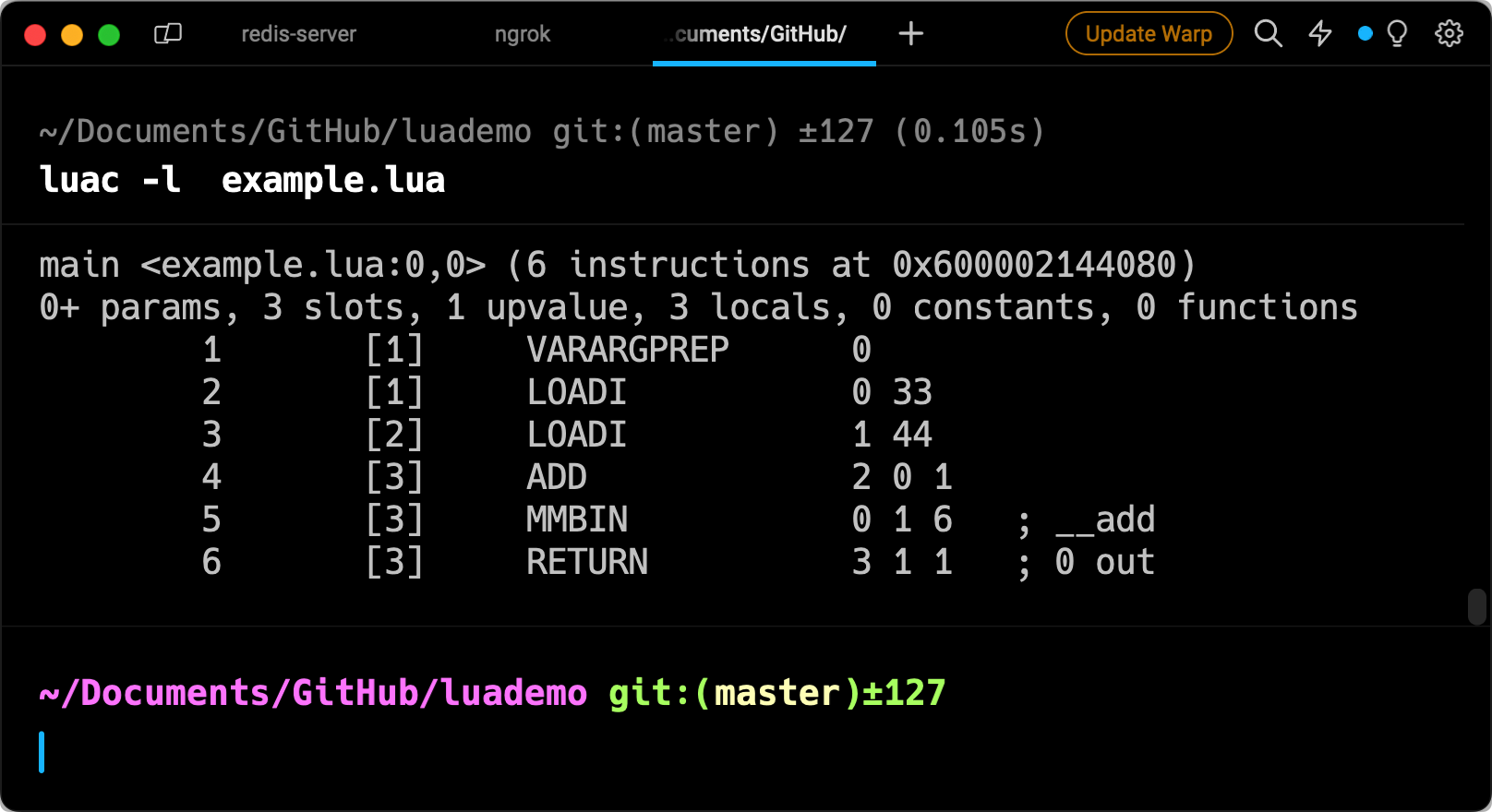
栈虚拟机和寄存器虚拟机,有什么不同?
本来这节内容是打算直接讲字节码指令的,但讲之前又必须得先讲指令集架构,而指令集架构又分为两种,一种是基于栈的,一种是基于寄存器的。 那不妨我们这节就单独来讲讲栈虚拟机和寄存器虚拟机,它们有什么不同࿰…...

Windows下基于fping进行批量IP测试
fping是Linux下一个很好用的IP测试工具,结合代码可以完成批量的IP测试,在网络调试中用途很广。本文是基于fping for Windows结合bat批处理,定制的测试脚本样例。 一、程序信息 本次测试使用fpingV5.1 for Windows版,版本信息如下…...

一款实用的Word文档图片转换与水印保护工具
目录 前言软件功能简介软件实现方法及关键代码 1. Word 文档转图片的实现2. 图片水印添加功能3. 生成数字指纹(哈希值)4. 保存图片信息到 JSON 文件 软件的实际使用场景软件操作指南 1. 下载和安装2. 操作流程 总结 1,前言 在日常办公和内…...
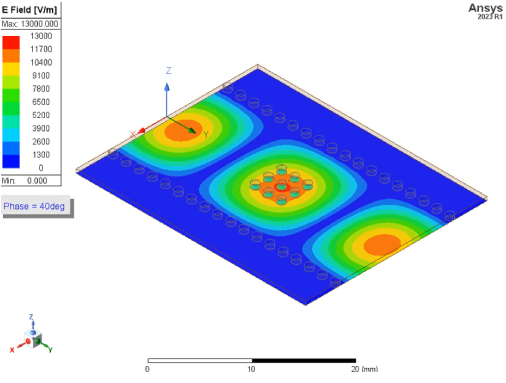
优化用于传感应用的衬底集成波导技术
ANSYS HFSS 是一款功能强大的电磁仿真软件,支持为微流体生物传感器应用设计和分析衬底集成波导 (SIW) 技术。它为快速设计优化、材料选择、系统集成和虚拟原型制作提供了一个强大的平台。借助 ANSYS HFSS,研究人员和工程师可以高效…...

Java多态特性的向上转型
Java的多态特性通过向上转型来实现。向上转型指的是将子类对象赋值给父类引用变量的操作。这样做的好处是可以使用父类引用变量来调用子类对象的方法。 例如,有一个父类Animal和一个子类Dog,可以这样进行向上转型: Animal animal new Dog(…...

C++ 判断语句的深入解析
C 判断语句的深入解析 C 是一种广泛使用的编程语言,以其高效性和灵活性著称。在 C 中,判断语句是控制程序流程的关键组成部分,它们允许程序根据不同的条件执行不同的代码路径。本文将深入探讨 C 中的判断语句,包括 if、else if、…...

15分钟学 Go 第 33 天:项目结构
第33天:项目结构 目标:了解Go项目的典型结构 在Go语言的开发中,项目结构的合理性直接影响着代码的可维护性、可扩展性和团队协作效率。本篇文章将深入探讨Go语言的典型项目结构,并提供实际示例代码和相关的流程图。 一、Go项目…...

conda迁移虚拟环境路径
方法一:使用软连接 ln -s ~/Anaconda3/envs /new/path/envs 方法二:修改~/.condarc文件 1.打开~/.condarc文件 #添加下面参数 envs_dirs: - /newpath/anaconda3/envs pkgs_dirs: - /newpath/anaconda3/pkgs 2. source ~/.bashrc 3.查看是否成功con…...

(八)JavaWeb后端开发——Tomcat
目录 1.Web服务器概念 2.tomcat 1.Web服务器概念 服务器:安装了服务器软件的计算机服务器软件:接收用户的请求,处理请求,做出响应web服务器软件:在web服务器软件中,可以部署web项目,让用户通…...
yocto中通常不直接修改提供的recipes的bb文件
不直接在 Yocto 官方提供的 recipe 中修改 通常是创建新的 metadata 和 recipe 来配置相关软件编译等过程 主要有以下几个原因: 1. 便于维护和升级 隔离自定义修改:Yocto 官方的 recipe 可能会随着版本更新而变化。如果直接修改官方 recipe࿰…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...
