常用滤波算法(二)-中位值滤波法
文章目录
- 一、中位值滤波法简介
- 二、C语言实现中位值滤波法
- 三、程序说明
- 信号初始化:
- 滤波窗口大小:
- 内存分配:
- 中位值滤波函数:
- 中位值计算函数:
- 内存释放:
- 四、总结
中位值滤波法,作为一种非线性滤波方法,能够有效去除信号中的噪声,尤其适用于处理脉冲噪声或随机噪声。
一、中位值滤波法简介
中位值滤波法的基本思想是用信号中某一点附近的一个邻域内所有点的中位值来代替该点的值。这种方法能够有效地抑制信号中的随机噪声和脉冲噪声,因为它依赖于数据的排序,而非数据的算术平均值。因此,即使噪声幅度较大,中位值滤波也能保持良好的滤波效果。
二、C语言实现中位值滤波法
下面是一个简单的C语言程序,用于实现一维信号的中位值滤波。
#include <stdio.h>
#include <stdlib.h>
// 函数声明
void medianFilter(int* signal, int signalLength, int filterSize, int* filteredSignal);
int median(int* array, int size);
int main() {
// 示例信号(含噪声)
int signal[] = {10, 12, 2, 20, 30, 25, 3, 18, 15, 14};
int signalLength = sizeof(signal) / sizeof(signal[0]);
int filterSize = 3; // 滤波窗口大小
// 验证滤波窗口大小是否为奇数
if (filterSize % 2 == 0) {printf("滤波窗口大小应为奇数。\n");return -1;
}// 分配内存给滤波后的信号
int* filteredSignal = (int*)malloc(signalLength * sizeof(int));
if (filteredSignal == NULL) {printf("内存分配失败。\n");return -1;
}// 应用中位值滤波
medianFilter(signal, signalLength, filterSize, filteredSignal);// 打印滤波后的信号
printf("滤波后的信号:\n");
for (int i = 0; i < signalLength; i++) {printf("%d ", filteredSignal[i]);
}
printf("\n");// 释放内存
free(filteredSignal);return 0;
}
// 中位值滤波函数
void medianFilter(int* signal, int signalLength, int filterSize, int* filteredSignal) {
int halfWindow = filterSize / 2;
for (int i = 0; i < signalLength; i++) {int* window = (int*)malloc((filterSize) * sizeof(int));if (window == NULL) {printf("内存分配失败。\n");exit(-1);}// 获取当前窗口内的信号值int count = 0;for (int j = -halfWindow; j <= halfWindow; j++) {int index = i + j;// 处理边界情况if (index >= 0 && index < signalLength) {window[count++] = signal[index];}}// 计算中位值filteredSignal[i] = median(window, count);// 释放窗口内存free(window);
}
}
// 计算数组的中位值
int median(int* array, int size) {
int* temp = (int*)malloc(size * sizeof(int));
if (temp == NULL) {
printf(“内存分配失败。\n”);
exit(-1);
}
// 复制并排序数组
for (int i = 0; i < size; i++) {temp[i] = array[i];
}
for (int i = 0; i < size - 1; i++) {for (int j = i + 1; j < size; j++) {if (temp[i] > temp[j]) {int swap = temp[i];temp[i] = temp[j];temp[j] = swap;}}
}// 获取中位值
int medianValue = temp[size / 2];// 释放临时数组内存
free(temp);return medianValue;
}
三、程序说明
信号初始化:
在main函数中,我们定义了一个包含噪声的示例信号。
滤波窗口大小:
我们设置了一个滤波窗口大小filterSize,并验证其是否为奇数,因为中位值滤波的窗口大小通常是奇数。
内存分配:
为滤波后的信号分配内存。
中位值滤波函数:
medianFilter函数遍历信号中的每个点,提取当前点附近窗口内的信号值,并计算这些值的中位值,以替换当前点的值。
中位值计算函数:
median函数负责计算一个数组的中位值。首先,它复制数组并对其进行排序,然后返回排序后数组的中位值。
内存释放:
在程序结束前,释放分配的内存。
四、总结
中位值滤波法是一种简单而有效的非线性滤波技术,特别适用于处理含有脉冲噪声的信号。本文通过一个C语言实例,详细展示了中位值滤波法的实现步骤,包括信号初始化、滤波窗口大小设置、内存分配与释放、中位值计算等关键步骤。希望这个实例能帮助读者更好地理解中位值滤波法的原理与应用。
相关文章:
-中位值滤波法)
常用滤波算法(二)-中位值滤波法
文章目录 一、中位值滤波法简介二、C语言实现中位值滤波法三、程序说明信号初始化:滤波窗口大小:内存分配:中位值滤波函数:中位值计算函数:内存释放: 四、总结 中位值滤波法,作为一种非线性滤波…...

HCIP--以太网交换安全(总实验)
实验背景 假如你是公司的网络管理员,为了提高公司网络安全性,你决定在接入交换机部署一些安全技术:端口隔、端口安全、DHCP snooping、IPSG。 实验拓扑图 实验的要求: 1.在R1、R2连接在GE0/0/1和GE0/0/2接口下,均划…...

C语言 | Leetcode C语言题解之第519题随机翻转矩阵
题目: 题解: typedef struct {unsigned long long val;UT_hash_handle hh; } Hash;typedef struct {Hash *hash;int n_rows;int n_cols; } Solution, SL;Solution* solutionCreate(int n_rows, int n_cols) {SL *obj malloc(sizeof(SL));obj->hash …...
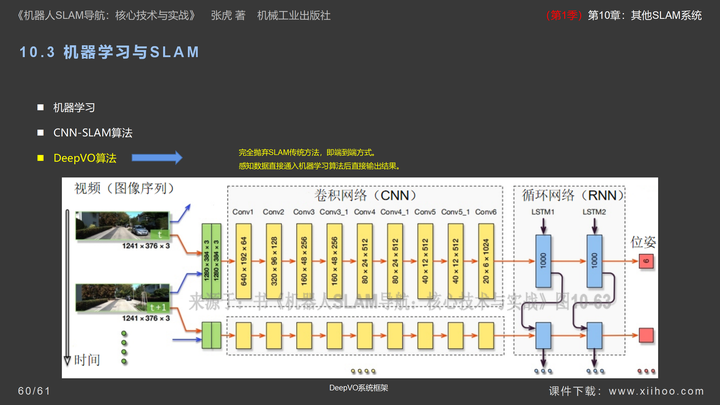
《机器人SLAM导航核心技术与实战》第1季:第10章_其他SLAM系统
视频讲解 【第1季】10.第10章_其他SLAM系统-视频讲解 【第1季】10.1.第10章_其他SLAM系统_RTABMAP算法-视频讲解 【第1季】10.2.第10章_其他SLAM系统_VINS算法-视频讲解 【第1季】10.3.第10章_其他SLAM系统_机器学习与SLAM-视频讲解 第1季:第10章_其他SLAM系统 …...

《双指针篇》---快乐数
题目传送门 1.创建一个bitsum函数用于得到这个数每位的平方和。 2.令快指针等于bitsum(n) 3.慢指针等于n。 逐步令 fast bitSum(bitSum(fast)); slow bitSum(slow); 若最后fast等于slow,则且等于1.则return true。 否则return false。 cla…...

U盘引导丢失问题的处理办法
项目背景:在使用自制的u盘系统的时候经常遇到引导丢失的问题,那么咱们怎么解决这个问题呢,首先第一步通过手动引导u盘 进入系统,同时再进行引导区的修复这样u盘系统就可以正常工作了。 1 进入grub 的提示符下面,首先…...

layui tree customSelet选中的内容重写,查找父级
layui tree customSelet选中的内容重写,查找父级 需要重新源码 // 递归查找函数 // tree 所有数据 ,nodeId选中数据id值 function findParent(tree, nodeId, parent null) {for (let i 0; i < tree.length; i) {if (tree[i].id nodeId) {return …...

Maven 插件
Maven 插件 Maven 是一个强大的项目管理和构建自动化工具,广泛应用于 Java 项目中。它通过插件来实现各种功能,如编译、测试、打包、部署等。Maven 插件是 Maven 的核心组成部分,它们扩展了 Maven 的功能,使其能够执行各种任务。…...

MybatisPlus入门(七)MybatisPlus-DQL编程控制
一、查询投影 查询投影:查出来的东西有多少字段,设置查询出来的结果长什么样,查出的字段控制; 查询投影适用于lamda格式,使用select 查询 lqw.select(User::getId,User::getName,User::getAge); 代码示例࿱…...

K8S概念及其常见组件和整体架构
1.概念 什么是Kubernetes 官网:Kubernetes 文档 | Kubernetes K8S的本质是一组服务器集群,可以在对应服务器集群的每个节点上运行程序,来对节点中的容器进行管理 类似Master-Work方式,每个服务器上安装特定的K8S组件,…...

LabVIEW继电器视觉检测系统
随着制造业的自动化与高精度要求不断提升,传统的人工检测方法逐渐难以满足高效和高精度的需求。特别是在航空航天、医疗设备等高端领域,密封继电器推动杆部件的质量直接影响到设备的性能与可靠性。LabVIEW自动化视觉检测系统,能对推动杆部件进…...

linux操作系统进程
linux操作系统是对下的软硬件进行管理,为了能够对上提供稳定,快速,安全的服务而诞生的软件。 广义上的操作系统是包含搭载在操作系统上的软件和函数库等文件的。 狭义上的操作系统就是操作系统内核,进行进程管理,文件…...

jeecgbootvue2菜单路由配置静态文件夹(public)下的html
需求:想要在菜单配置src/assets/iconfont/chart.html显示页面(目的是打包上线以后运维依然可以修改数据) 官网没有相关数据:菜单配置说明 JeecgBoot 开发文档 看云 问题现象: 我把文件放在src/assets/iconfont/chart.html然后在vue中作为 iframe 的 src 属性&am…...

PHP反序列化原生类字符串逃逸框架反序列化利用
PHP反序列化 概念 序列化的原因:为了解决开发中数据传输和数据解析的一个情况(类似于要发送一个椅子快递,不可能整个椅子打包发送,这是非常不方便的,所以就要对椅子进行序列化处理,让椅子分成很多部分在一起打包发送…...

6.1、属性动画
使用显式动画产生布局更新动画 1.旋转动画 只修改对应的属性 rotate({angle: this.angle}) 即可达到效果 动画效果 对应实现代码 @Entry @Component struct AnimationPage {@State angle:number = 0aboutToAppear() {...

v-model还可以作用于其他表单元素的使用
1、文本输入框 直接双向绑定输入的元素值 初始化默认值为空字符串 2、复选按钮 直接双向绑定输入的元素值 初始化默认值为flase,不选中 3、单选按钮, 1.使用name分组,产生互斥效果。 2.使用value存值, 3再用v-model双向绑定…...

最短路的求解
实验类型:◆验证性实验 ◇综合性实验 ◇设计性实验 实验目的:学会使用Matlab求解最短路。 实验内容:1.熟练运用Floyd算法;2. 熟练运用Dijkstra算法;3.利用Matlab编程实现最短路的计算。 例1:已知无向图…...
-- 异常 字符串)
四:java 基础知识(4)-- 异常 字符串
目录 1. 异常处理 1.1 什么是异常 1.2 异常的类型 1.2.1 检查异常 1.2.2 运行时异常 1.3 异常的捕获与处理 1.3.1 try-catch 语句 1.3.2 finally 块 1.3.3 throw 和 throws 关键字 1.4 自定义异常 1.5 异常的最佳实践 2. 字符串 2.1 String 类的概述 2.2 字符串的…...

Uniapp 实现app自动检测更新/自动更新功能
实现步骤 配置 manifest.json 在 manifest.json 中设置应用的基本信息,包括 versionName 和 versionCode。 一般默认0.0.1,1. 服务器端接口开发 提供一个 API 接口,返回应用的最新版本信息,版本号、下载链接。客户端检测更新 使…...

7.0、RIP
RIP (Routing Information Protocol) 简介 RIP是由Xerox在20世纪70年代开发的,最初定义在RFC1058中。RIP用两种数据包传输更新:更新和请求,每个有RIP功能的路由器在默认情况下,每隔30s利用UDP520端口向与它直连的网络邻居广播(RIP1)或组播(R…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...
