最短路的求解
实验类型:◆验证性实验 ◇综合性实验 ◇设计性实验
实验目的:学会使用Matlab求解最短路。
实验内容:1.熟练运用Floyd算法;2. 熟练运用Dijkstra算法;3.利用Matlab编程实现最短路的计算。
例1:已知无向图G如下所示,试利用Floyd算法求任意两点间的最短路。

例2:试利用Dijkstra算法求下面有向图G中从点v1到v9的最短路。

实验原理:
Floyd算法:
1.使用范围
①求任意两结点的最短路径;
②有向图、无向图、混合图。
2.基本思想
直接在网络图的权矩阵W WW中用插入顶点的方法依次递推地构造出n nn个矩阵D ( 1 ) , D ( 2 ) , … , D ( n ) D(1),D(2),…,D(n)D(1),D(2),…,D(n),D ( n ) D(n)D(n)是网络图的最短距离矩阵,同时引入一个路由矩阵记录任意两点之间的最短路径。
3.算法步骤
设D i j 为结点v i 到v j的距离;P i j为结点v i到v j路径上v i 的后继点;
W为权矩阵。
第1步:∀i,j,D ij=W ij,P ij=j,k=1;(赋初值)
第2步:∀i,j,若D i k + D k j < D i j,则D i j = D i k + D k j,P i j = P i k,k = k+1(更新D,PD,PD,P)
第3步:重复第2步,直到k=n+1。
Dijkstra算法:
算法特点:
迪科斯彻算法使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题,算法最终得到一个最短路径树。该算法常用于路由算法或者作为其他图算法的一个子模块。
算法的思路:
Dijkstra算法采用的是一种贪心的策略,声明一个数组dis来保存源点到各个顶点的最短距离和一个保存已经找到了最短路径的顶点的集合:T,初始时,原点 s 的路径权重被赋为 0 (dis[s] = 0)。若对于顶点 s 存在能直接到达的边(s,m),则把dis[m]设为w(s, m),同时把所有其他(s不能直接到达的)顶点的路径长度设为无穷大。初始时,集合T只有顶点s。
然后,从dis数组选择最小值,则该值就是源点s到该值对应的顶点的最短路径,并且把该点加入到T中,OK,此时完成一个顶点。
然后,我们需要看看新加入的顶点是否可以到达其他顶点并且看看通过该顶点到达其他点的路径长度是否比源点直接到达短,如果是,那么就替换这些顶点在dis中的值。
然后,又从dis中找出最小值,重复上述动作,直到T中包含了图的所有顶点。
实验步骤:
1. 上机实验前先编写出程序代码
2. 录入、编辑程序
3. 调适程序至正确运行
4. 记录运行时的输入和输出
5. 对程序做进一步完善
程序代码:
例1:
d=[0 3 5 Inf Inf Inf
3 0 1 2 2 Inf
5 1 0 Inf 4 Inf
Inf 2 Inf 0 2 4
Inf 2 4 2 0 2
Inf Inf Inf 4 2 0];
n=length(d);
U=d;
S=zeros(n,n);
for i=1:n
for j=1:n
S(i,j)=j;
end
end
for i=1:n
for j=1:n
for m=1:n
if U(i,j)>U(i,m)+U(m,j)
U(i,j)=U(i,m)+U(m,j);
S(i,j)=S(i,m);
end
end
end
end
S
U
例2:
W=input('此程序有关MST,请输入权矩阵:');
[i,j,s] = find(W);
ss = [i';j';s'];
dg = sparse(ss(1,:),ss(2,:),ss(3,:));
dg(9,9)=0;
h=view(biograph(dg,[],'ShowWeights','on'));
[dist,path,~]=graphshortestpath(dg,1,9,'Directed','true')
set(h.Nodes(path),'Color',[1 0.4 0.4]);
edges=getedgesbynodeid(h,get(h.Nodes(path),'ID'));
set(edges,'LineColor',[1 0 0]);
set(edges,'LineWidth',2);
实验运行结果界面:


实验总结:
本次实验通过Floyd算法和Dijkstra算法求解了最短路径问题,掌握了它们的基本原理和实现方法。Floyd算法适用于求解任意两点间的最短路径,而Dijkstra算法适用于求解从指定起点到指定终点的最短路径。
在适用范围上:
Floyd算法适用于求解任意两点间的最短路径,可以处理带负权边的图,但不能处理带负权回路的图。Dijkstra算法适用于求解从指定起点到其他所有点的最短路径,不能处理带负权边的图。
在稳定性上:
Floyd算法是一种动态规划算法,可以保证找到全局最优解。但是Dijkstra算法是一种贪心算法,每次选择当前最短路径的顶点,不能保证全局最优解,但对于非负权图可以保证最短路径是最优的。
在实现难度上:
Floyd算法相对简单,只需使用三重循环更新距离矩阵即可。Dijkstra算法在实现时需要使用优先队列等数据结构,相对复杂一些。
学到很多新的东西,路漫漫其修远兮,吾将上下而求索。加油!
相关文章:

最短路的求解
实验类型:◆验证性实验 ◇综合性实验 ◇设计性实验 实验目的:学会使用Matlab求解最短路。 实验内容:1.熟练运用Floyd算法;2. 熟练运用Dijkstra算法;3.利用Matlab编程实现最短路的计算。 例1:已知无向图…...
-- 异常 字符串)
四:java 基础知识(4)-- 异常 字符串
目录 1. 异常处理 1.1 什么是异常 1.2 异常的类型 1.2.1 检查异常 1.2.2 运行时异常 1.3 异常的捕获与处理 1.3.1 try-catch 语句 1.3.2 finally 块 1.3.3 throw 和 throws 关键字 1.4 自定义异常 1.5 异常的最佳实践 2. 字符串 2.1 String 类的概述 2.2 字符串的…...

Uniapp 实现app自动检测更新/自动更新功能
实现步骤 配置 manifest.json 在 manifest.json 中设置应用的基本信息,包括 versionName 和 versionCode。 一般默认0.0.1,1. 服务器端接口开发 提供一个 API 接口,返回应用的最新版本信息,版本号、下载链接。客户端检测更新 使…...

7.0、RIP
RIP (Routing Information Protocol) 简介 RIP是由Xerox在20世纪70年代开发的,最初定义在RFC1058中。RIP用两种数据包传输更新:更新和请求,每个有RIP功能的路由器在默认情况下,每隔30s利用UDP520端口向与它直连的网络邻居广播(RIP1)或组播(R…...
C#与C++结构体的交互
C#在和C进行交互时,有时候会需要传递结构体。 做一些总结,避免大家在用的时候踩坑。 一般情况 例如我们在C里定义了一个struct_basic结构体 1 struct struct_basic 2 { 3 WORD value_1; 4 LONG value_2; 5 DWORD value_3; 6 UINT v…...

sql纵表转横表
项目上有一个需求(例子): 用户表 user{ id, name, workCode } id name workCode 1 张三 WC1001 2 李四 WC1002 工作信息表 work{ id, name, workCode, workTimeSun } id name …...

数据采集-Kepware OPCUA 服务器实现
KepserverEX OPC UA server设置 系列文章目录 数据采集-Kepware 安装证书异常处理 目录 KepserverEX OPC UA server设置系列文章目录一、OPC UA(OPC Unified Architecture)二、防火墙的配置三、配置KepserverEX的OPC UA3.1 启用远程连接3.2 启动OPCUA服务器接口 四、管理OPCU…...

初识计算机网络
🌎初识计算机网络 文章目录: 初识计算机网络 计算机网络背景 网络协议 初识协议 制定协议标准的组织或公司 OSI七层模型 操作系统和计算机网络关系 再谈协议 网络传输的基本流程 …...

Oracle 第11章:异常处理
在 Oracle PL/SQL 中,异常处理是一个重要的概念,它用于管理程序执行过程中可能发生的错误或特殊情况。异常可以是系统预定义的,也可以是由用户自定义的。 异常类型与处理机制 PL/SQL 提供了两种类型的异常: 预定义异常…...

导航栏渐变色iOS
- (void)viewDidLoad {[super viewDidLoad];// 设置导航栏属性self.navigationBar.translucent NO;[self.navigationBar setTitleTextAttributes:{NSForegroundColorAttributeName : [UIColor whiteColor], NSFontAttributeName:[UIFont boldSystemFontOfSize:28]}];// 修复iO…...

mysql读写分离
一、proxysql实现mysql读写分离 二、mycat...

计算机的错误计算(一百四十二)
摘要 本节探讨 MATLAB中 附近数的正弦函数的计算精度问题。 例1. 已知 计算 与 直接贴图吧: 另外, 16位的正确值分别为 -0.3077518861551721e-8 与 0.4106402475009074e-3(ISRealsoft 提供)。 容易看出,MATLAB的…...

利用大模型辅助科研论文写作·第一期|论文写作·24-11-02
小罗碎碎念 从这期推文开始,开一个新的系列——如何利用大语言模型辅助论文写作。 我目前的推文主要都集中于分享已经发表的论文,前期背景积累到一定程度以后,我们要动手做实验然后写自己的论文。如果从头到尾,全都自己写…...

JavaScript。—关于语法基础的理解—
一、程序控制语句 JavaScript 提供了 if 、if else 和 switch 3种条件语句,条件语句也可以嵌套。 (一)、条件语句 1、单向判断 : if... (1)概述 < if >元素用于在判断该语句是否满足特定条…...

Tomcat 11 下载/安装 与基本使用
为什么要使用Tomcat? 使用Apache Tomcat的原因有很多,以下是一些主要的优点和特点: 1. 开源与免费 Tomcat是一个完全开源的项目,任何人都可以免费使用。它由Apache软件基金会维护,拥有一个活跃的社区,这…...

Linux系统时间服务——Chrony服务器
文章目录 Linux系统时间服务——Chrony服务器前言时间同步的重要性Linux系统的两种时钟系统时钟(System Clock)相关命令硬件时钟 (RTC - Real Time Clock)相关命令 Chrony介绍NTP Chronyc相关命令服务管理相关命令chronyc 基本命令时间校正和控制命令NTP…...
)
C# 接口(Interface)
C# 接口(Interface) 接口在C#中是一种非常重要的概念,它定义了一个约定,实现该接口的类必须遵循这个约定。接口可以包含方法、属性、事件和索引器,但不包含实现。这使得接口成为定义抽象行为的理想选择。在本文中&…...

《高频电子线路》—— 电容三端LC振荡器
文章内容来源于【中国大学MOOC 华中科技大学通信(高频)电子线路精品公开课】,此篇文章仅作为笔记分享。 电容三端LC振荡器 基本原理(考毕兹电路) 反馈电压从C2上取得,作为输入电压,形成正反馈&a…...

leetcode35.搜索插入位置
1)题目描述: 2)本题要求使用 时间复杂度O(log n)的算法,这里使用二分查找的方法,这道题本身不复杂,但是,在使用递归调用时,笔者经常把递归结束的边界搞错,这里给出几版代…...
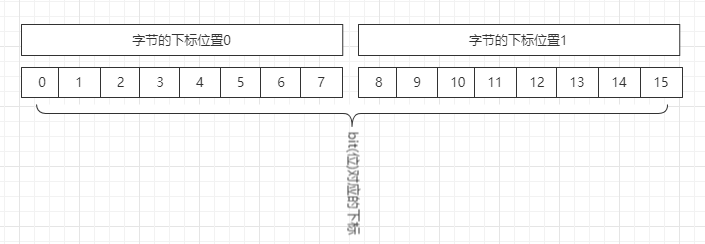
Redis全系列学习基础篇之位图(bitmap)常用命令的解析
文章目录 描述常用命令及解析常用命令解析 应用场景统计不确定时间周期内用户登录情况思路分析实现 统计某一特定时间内活跃用户(登录一次即算活跃)的数量思路分析与实现 描述 bitmap是redis封装的用于针对位(bit)的操作,其特点是计算效率高,占用空间少,常被用来统计…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...
