leetcode35.搜索插入位置
1)题目描述:

2)本题要求使用 时间复杂度O(log n)的算法,这里使用二分查找的方法,这道题本身不复杂,但是,在使用递归调用时,笔者经常把递归结束的边界搞错,这里给出几版代码,做一下讨论
第1版代码:
class Solution {
public:int findMid(vector<int>& nums, int l, int r, int target) {int mid = (l+r)/2;if(nums[mid] == target) {return mid;}else if(l == r) {if(nums[mid] < target) {return mid+1;}else {return mid;}}else if(l > r) {// array is [3, 5, 7, 9, 10], target=8// ...// l=3, r=4 m=3 nums[mid]>target// l=3, r=2 m=2// when l > r, just return lreturn l;}else {if(nums[mid] < target) {l = mid + 1;}else {r = mid - 1;}}return findMid(nums, l, r, target);}int searchInsert(vector<int>& nums, int target) {return findMid(nums, 0, nums.size()-1, target);}
};这里需要注意的一点是,如果需要继续二分查找,则需要更新左右边界,笔者直觉上认为,如果nums[mid] < target,将左边界更新为mid+1,如果nums[mid] > target,将右边界更新为mid-1,但是在实际执行程序时,这样做可能会出现左边界>右边界的情况,程序进入无限循环,如下图所示:

所以在原始代码的基础上增加了对于"左边界>右边界的情况"的简单处理,当然了,之所以可以简单处理,是因为出现这种情况时,搜索插入位置可以确定了。
第2版代码:
class Solution {
public:int findMid(vector<int>& nums, int l, int r, int target) {int mid = (l+r)/2;if(nums[mid] == target) {return mid;}else if(l == r) {if(nums[mid] < target) {return mid+1;}else {return mid;}}else {if(nums[mid] < target) {l = mid + 1;}else {r = mid;}}return findMid(nums, l, r, target);}int searchInsert(vector<int>& nums, int target) {return findMid(nums, 0, nums.size()-1, target);}
};在第1版代码的基础上,笔者在想,是否可以避免"左边界>右边界的情况",同时为了要找到插入位置,还要不断地缩小搜索空间,在上面列举的出现"左边界>右边界的情况"的例子中,最后,l=3,r=4,m=3,最后nums[mid]>target,需要将r更新为mid-1,那么这里我们可以做保守处理,将r更新为mid。如果l与r相同,代码做了详尽处理。l=mid+1、r=mid-1的边界更新策略就是没有很好地处理l+1=r的情况,这里检查一下l=mid+1、r=mid的边界更新策略是否能处理r-l=1的情况。如果r-l=1,则mid=(l+l+1)/2=l,如果nums[mid]=target,则搜索插入位置是mid,如果nums[mid]<target,则l保持不变,r更新为mid(上一步的l),如果nums[mid]>target,则l更新为mid+1(上一步的l+1),r保持不变。如果r-l>1,在不断地缩小搜索空间后,总会进入到l=r或r-l=1的情况。
第3版代码:
class Solution {
public:int findMid(vector<int>& nums, int l, int r, int target) {int mid = (l+r)/2;if(mid*2+1 == l+r) {mid++;}if(nums[mid] == target) {return mid;}else if(l == r) {if(nums[mid] < target) {return mid+1;}else {return mid;}}else {if(nums[mid] < target) {l = mid;}else {r = mid - 1;}}return findMid(nums, l, r, target);}int searchInsert(vector<int>& nums, int target) {return findMid(nums, 0, nums.size()-1, target);}
};这里将第3版代码与第2版做对比,讨论mid与左右边界的关系、以及左右边界的更新策略,当l+r不能整除时,(l+r)/2取下整,举个例子,如果l=3,r=4,则mid应该是3.5,当然计算机默认策略是取下整3,是小于3.5的一个整数,所以在r-l=1时,l与mid是重合的,如果是左边界更新,可以将其更新为mid+1,向右边界靠近,如果是右边界更新,只能将其更新为mid(如果更新为mid-1,则可能出现左边界>右边界的情况),也可以理解,mid=(l+r)/2可能在左右边界的中间位置,也有可能偏左。第3版代码就是在(l+r)不能整除2的情况下,让mid偏右,这时左右边界的更新策略可以改为l=mid,r=mid-1。
4)关于递归,要仔细考虑到自己的代码最后结束的情况有哪几种,这样才能避免未预期的情况。
相关文章:

leetcode35.搜索插入位置
1)题目描述: 2)本题要求使用 时间复杂度O(log n)的算法,这里使用二分查找的方法,这道题本身不复杂,但是,在使用递归调用时,笔者经常把递归结束的边界搞错,这里给出几版代…...
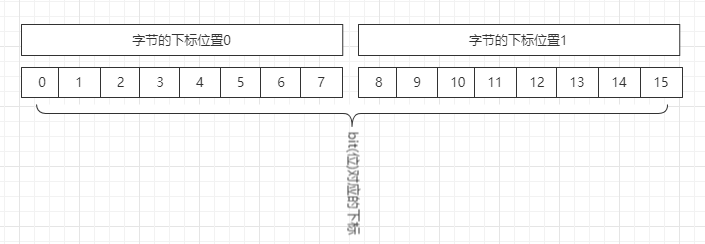
Redis全系列学习基础篇之位图(bitmap)常用命令的解析
文章目录 描述常用命令及解析常用命令解析 应用场景统计不确定时间周期内用户登录情况思路分析实现 统计某一特定时间内活跃用户(登录一次即算活跃)的数量思路分析与实现 描述 bitmap是redis封装的用于针对位(bit)的操作,其特点是计算效率高,占用空间少,常被用来统计…...

Copilot功能
Copilot 1、简介:Copilot是由GitHub与OpenAI共同开发的一款AI编程助手,旨在帮助开发者提高工作效率,改善代码质量。 2、主要功能包括: 1.代码补全:Copilot可以在开发者编写代码时提供代码建议,包括函数、循…...

《GBDT 算法的原理推导》 11-13初始化模型 公式解析
本文是将文章《GBDT 算法的原理推导》中的公式单独拿出来做一个详细的解析,便于初学者更好的理解。 公式(11-13)是GBDT算法的第一步,它描述了如何初始化模型。公式如下: f 0 ( x ) arg min c ∑ i 1 N L ( y i , c ) f_0(x) \arg \m…...

# Easysearch 与 LLM 融合打造高效智能问答系统
LangChain通过提供统一的抽象层和丰富的工具,极大地简化了LLM应用程序的开发过程,使得开发者能够更加专注于业务逻辑。RAG技术则通过索引和检索生成两步流程,利用最新数据或私有数据作为背景信息来增强大模型的推理能力。然而,对于…...

本地可以插入表记录,生产不能插入表记录
先说解决方案: 切面没有注入容器,在切面这加上Component详情: 大致是这样一个方法,本地运行会插入数据到sys_log表,但部署到服务器上就不会插入,而服务部署三年多了,一个表一直是空的居然没人…...

11.Three.js使用indexeddb前端缓存模型优化前端加载效率
11.Three.js使用indexeddb前端缓存模型优化前端加载效率 1.简述 在使用Three.js做数字孪生应用场景时,我们常常需要用到大量模型或数据。在访问我们的数字孪生应用时,每次刷新都需要从web端进行请求大量的模型数据或其他渲染数据等等,会极大…...

功能测试:方法、流程与工具介绍
功能测试是对产品的各功能进行验证的一种测试方法,旨在确保软件以期望的方式运行并满足设计需求。以下是对功能测试的详细解释: 一、定义与目的 定义:功能测试(Functional Testing),也称为行为测试&#…...

【Orange Pi 5 Linux 5.x 内核编程】-设备驱动中的sysfs
设备驱动中的sysfs 文章目录 设备驱动中的sysfs1、sysfs介绍2、内核对象(kobject)介绍3、设备驱动中的SysFS31 在/sys中创建目录3.2 创建sysfs文件3.2.1 创建属性3.2.2 创建sysfs文件4、驱动程序实现5、驱动验证1、sysfs介绍 sysfs是内核导出的虚拟文件系统,类似于/proc。sys…...

微信小程序-全局数据共享/页面间通信
一.全局数据共享 声明全局的变量,在app.js文件里 App({//全局共享的数据globalData:{token:},//设置全局数据setToken(token){this.globalData.tokentoken}})使用 getApp() 获取全局App实例 //返回全局唯一的APP实例 const appInstancegetApp()Page({login(){con…...
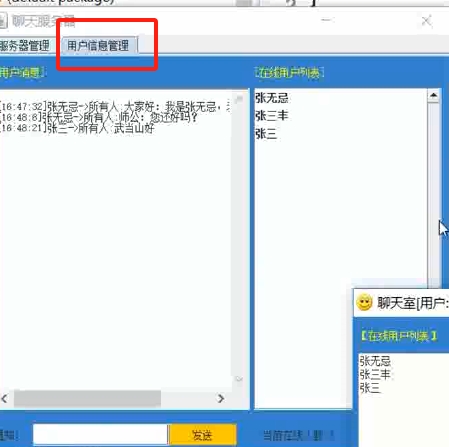
java计算机毕设课设—Java聊天室(附源码、文章、相关截图、部署视频)
这是什么系统? 资源获取方式再最下方 java计算机毕设课设—Java聊天室(附源码、文章、相关截图、部署视频) Java聊天室系统是一个基于Java语言开发的在线即时通讯平台,旨在为用户提供一个简单、易用的实时交流环境。该系统支持多用户同时在线交流&…...

图像识别基础认识
import numpy as np import pandas as pd import matplotlib.pyplot as plt import cv2 %matplotlib inline读取图像 img = cv2.imread(shuzi.png) # 显示图像 cv2.imshow(shuzi, img) # 设置窗口大小 #cv2.resizeWindow(shuzi, 800, 600) # 设置宽为800,高为600 cv2.waitKe…...

使用 OpenCV 读取和显示图像与视频
概述 OpenCV 是一个强大的计算机视觉库,广泛应用于图像处理和视频处理等领域。本文将详细介绍如何使用 OpenCV 在 Python 中读取和显示图像以及视频,并通过具体的代码示例来展示整个过程。 环境准备 在开始之前,请确保已经安装了 OpenCV 库…...

【1】Elasticsearch 30分钟快速入门
文章目录 一、Elasticsearch 基本概念及工作原理(一)基本概念(二)工作原理二、Elasticsearch 原生 RESTful 方式的增删改查(一)创建索引(二)插入文档(三)查询文档(四)更新文档(五)删除文档(六)删除索引三、Python SDK 实现增删改查(一)安装 Elasticsearch Py…...

教材管理系统设计与实现
教材管理系统设计与实现 1. 系统概述 教材管理系统是一个基于PHP和SQL的Web应用程序,旨在为学校提供一个高效的教材管理平台。该系统可以帮助管理员录入教材信息、教师查询和申请教材、学生查询教材信息,提高教材管理的效率和透明度。 2. 技术栈 前端…...

软考(中级-软件设计师)数据库篇(1101)
第6章 数据库系统基础知识 一、基本概念 1、数据库 数据库(Database ,DB)是指长期存储在计算机内的、有组织的、可共享的数据集合。数据库中的数据按一定的数据模型组织、描述和存储,具有较小的冗余度、较高的数据独立性和扩展…...

安装nscd及glibc包冲突降级【centos7】
安装nscd及glibc包冲突降级【centos7】 一、查看当前glibc版本二、查找可用的glibc版本三、备份系统和数据四、降级glibc五、验证降级是否成功六、解决其他依赖问题七、测试和验证八、考虑使用容器技术endl [08:41:07 rootcentos7 ~]# yum -y install nscd Loaded plugins: fas…...

Qt字符编码
目前字符编码有以下几种: 1、UTF-8 UTF-8编码是Unicode字符集的一种编码方式(CEF),其特点是使用变长字节数(即变长码元序列、变宽码元序列)来编码。一般是1到4个字节,当然,也可以更长。 2、UTF-16 UTF-16是Unicode字符编码五层次…...
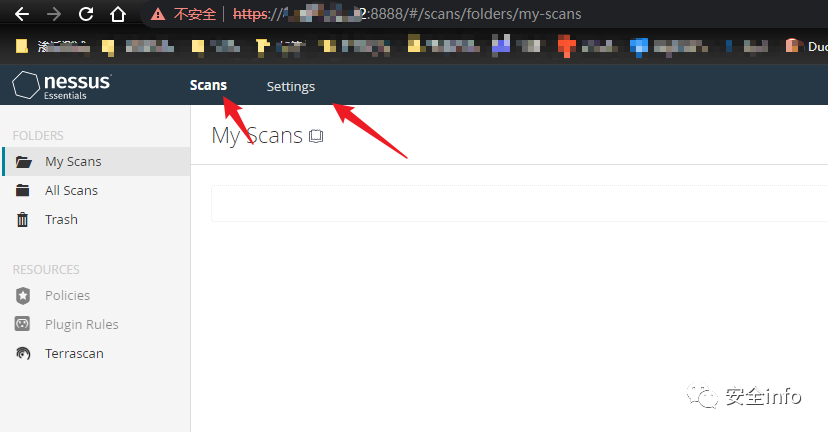
Ubuntu用docker安装AWVS和Nessus(含破解)
Ubuntu安装AWVS(更多搜索:超详细Ubuntu用docker安装AWVS和Nessus) 首先安装docker,通过dockers镜像安装很方便,且很快;Docker及Docker-Compose-安装教程。 1.通过docker search awvs命令查看镜像; docker search awvs…...

tauri开发中如果取消了默认的菜单项,复制黏贴撤销等功能也就没有了,解决办法
取消默认的菜单项:清除tauri默认的菜单项,让顶部的菜单menu不显示-CSDN博客 就是通过配置空菜单,让菜单不显示,但是这个引发的问题就是复制黏贴撤销等功能也就没有了,解决办法: 新增加编辑下的子菜单&…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...
