C#二叉树原理及二叉搜索树代码实现
一、概念
二叉树(Binary Tree)是一种树形数据结构,其中每个节点最多有两个子节点,分别称为左子节点和右子节点。二叉树的每个节点包含三个部分:一个值、一个指向左子节点的引用和一个指向右子节点的引用。
二、二叉树的基本概念
- 节点:二叉树中的每个元素称为节点。每个节点包含一个值以及指向其左子节点和右子节点的引用。
- 根节点:二叉树的顶端节点称为根节点。它是树中唯一没有父节点的节点。
- 子节点:每个节点可以有零个、一或两个子节点。子节点分为左子节点和右子节点。
- 叶节点:没有子节点的节点称为叶节点或终端节点。
- 内部节点:至少有一个子节点的节点称为内部节点。
- 高度:从根节点到某个节点的最长路径上的边数称为该节点的高度。树的高度是所有节点高度的最大值。
- 深度:从根节点到某个节点的路径上的边数称为该节点的深度。根节点的深度为0。
- 层次:树中所有深度相同的节点组成一层。根节点在第0层,其子节点在第1层,以此类推。
三、二叉树的类型
- 满二叉树:每个节点要么是叶节点,要么有两个子节点。
- 完全二叉树:除了最后一层外,每一层都是满的,并且最后一层的所有节点都尽可能地靠左排列。
- 二叉搜索树(BST):对于树中的每个节点,其左子树中的所有节点值都小于该节点的值,而其右子树中的所有节点值都大于该节点的值。
四、二叉树的作用
- 快速查找:二叉搜索树允许我们以O(log n)的时间复杂度进行查找操作。
- 排序:通过中序遍历,可以得到一个有序的元素列表。
- 动态集合:支持动态插入和删除操作,适用于需要频繁修改的数据集合。
- 表达式解析:二叉树常用于表示算术表达式,其中内部节点表示运算符,叶节点表示操作数。
五、二叉树的遍历
遍历是指访问树中每个节点的过程。常见的遍历方法包括:
- 前序遍历(Pre-order Traversal):先访问根节点,然后递归地访问左子树,最后递归地访问右子树。
- 中序遍历(In-order Traversal):先递归地访问左子树,然后访问根节点,最后递归地访问右子树。这种遍历方式特别适用于二叉搜索树,因为它会按升序访问所有节点。
- 后序遍历(Post-order Traversal):先递归地访问左子树,然后递归地访问右子树,最后访问根节点。
- 层次遍历(Level-order Traversal):按层次逐层访问节点,从上到下,从左到右。
六、二叉搜索树(Binary Search Tree, BST)
定义
二叉搜索树是一种特殊的二叉树,它满足以下性质:
- 对于树中的每个节点,其左子树中的所有节点值都小于该节点的值,而其右子树中的所有节点值都大于该节点的值。
特性
- 查找操作:由于二叉搜索树的性质,可以通过比较节点值快速定位目标节点,平均时间复杂度为O(log n)。
- 插入操作:新节点总是插入到叶节点的位置,保持二叉搜索树的性质。
- 删除操作:删除节点时需要考虑三种情况:
- 节点是叶节点:直接删除即可。
- 节点有一个子节点:用子节点替换被删除的节点。
- 节点有两个子节点:找到该节点的中序后继(右子树中的最小节点)或中序前驱(左子树中的最大节点),用它替换被删除的节点,然后删除该后继或前驱节点。
七、二叉搜索树代码实现
1、定义二叉树结构
/// <summary>/// 二叉树搜索树节点结构/// </summary>public class TreeNode{public int Value;public TreeNode? Left;public TreeNode? Right;public TreeNode(int value) {Value = value;Left = null;Right = null;}}2、定义二叉搜索树类,实现包括二叉搜索树的插入、删除、搜索、中序遍历等
/// <summary>
/// 二叉搜索树
/// </summary>
public class BinarySearchTree
{private TreeNode? root;public BinarySearchTree() { root = null; }//二叉树插入数据public void BinaryTreeInsert(int value){if (root == null){root = new TreeNode(value); }else{InsertRec(root, value);} }//递归插入数据到二叉树public void InsertRec(TreeNode node,int value){if(value < node.Value)//小于当前节点,往当前节点的左子树判断插入{if(node.Left == null){node.Left = new TreeNode(value);}else{InsertRec(node.Left, value);}}else if(value > node.Value)//大于当前节点,往当前节点的右子树判断插入{if(node.Right == null){node.Right = new TreeNode(value);}else{InsertRec(node.Right, value);}}else if (value == node.Value) //等于当前节点,重复不插入{return;}}//二叉树搜索public bool BinaryTreeSearch(int value){return SearchRec(root, value);}//递归搜索二叉树public bool SearchRec(TreeNode? node,int value){if(node == null){return false;}if (value < node.Value)//小于当前节点,往当前节点的左子树判断比较{return SearchRec(node.Left, value);}else if (value > node.Value){return SearchRec(node.Right, value);//大于当前节点,往当前节点的左子树判断比较}else{return true; }}//二叉树删除节点public void BinaryTreeRemove(int value){root = RemoveRec(root, value);}//递归删除二叉树节点public TreeNode? RemoveRec(TreeNode? node,int value){if (node == null){ return null; }if(value < node.Value){node.Left = RemoveRec(node.Left, value);}else if(value > node.Value){node.Right = RemoveRec(node.Right, value);}else{if(node.Left != null && node.Right != null){//如果需要删除的节点左右子节点都不为空,使用节点的右子树的最小节点替换当前节点TreeNode? minNode = FinMinNode(node.Right);if(minNode != null){node.Value = minNode.Value;node.Right = RemoveRec(node.Right, minNode.Value);}}else{TreeNode? tempNode = node.Left != null ? node.Left : node.Right;node = tempNode;}}return node;}//查找二叉树的最小节点public TreeNode? FinMinNode(TreeNode? node){if(node == null){return null;}while (node.Left != null) //往左子树找最小{ node = node.Left;}return node;}//遍历二叉树排序输出public List<int> InorderTraversal(){List<int> arry = new List<int>();InorderTraversalRec(root,arry);return arry;}public void InorderTraversalRec(TreeNode? node, List<int> arrys){if(node != null){InorderTraversalRec(node.Left , arrys);arrys.Add(node.Value);InorderTraversalRec(node.Right , arrys);}}//后序遍历public void PostOrderTraversal(){PostOrderTraversalRec(root);}public void PostOrderTraversalRec(TreeNode? node){if (node == null){return;}PostOrderTraversalRec(node.Right);PostOrderTraversalRec(node.Left);Console.WriteLine(node.Value);}//前序遍历public void PreOrderTraversal(){PreOrderTraversalRec(root);}public void PreOrderTraversalRec(TreeNode? node){if(root == null){return;}Console.WriteLine(node.Value);PreOrderTraversalRec(node.Left);PreOrderTraversalRec(node.Right);}
}八、二叉搜索树验证
1、编写验证代码:
static async Task Main(string[] args)
{BinarySearchTreeTest();
}/// <summary>
/// 二叉树测试
/// </summary>
static void BinarySearchTreeTest()
{var bst = new BinarySearchTree();bst.BinaryTreeInsert(35);bst.BinaryTreeInsert(13);bst.BinaryTreeInsert(23);bst.BinaryTreeInsert(45);bst.BinaryTreeInsert(78);bst.BinaryTreeInsert(4);bst.BinaryTreeInsert(17);bst.BinaryTreeInsert(89);bst.BinaryTreeInsert(67);Console.WriteLine("中序遍历(打印有序数组):");List<int> list = bst.InorderTraversal();foreach (int i in list){Console.WriteLine(i);}Console.WriteLine("\n");// 查找Console.WriteLine("Search for 45: " + bst.BinaryTreeSearch(45)); // 输出: TrueConsole.WriteLine("Search for 25: " + bst.BinaryTreeSearch(25)); // 输出: FalseConsole.WriteLine("\n");// 删除bst.BinaryTreeRemove(17);Console.WriteLine("删除17后,中序遍历(打印有序数组):");List<int> list1 = bst.InorderTraversal();foreach (int j in list1){Console.WriteLine(j);}
}2、运行验证

总结
相关文章:

C#二叉树原理及二叉搜索树代码实现
一、概念 二叉树(Binary Tree)是一种树形数据结构,其中每个节点最多有两个子节点,分别称为左子节点和右子节点。二叉树的每个节点包含三个部分:一个值、一个指向左子节点的引用和一个指向右子节点的引用。 二、二叉树…...

.eslintrc.js 的解释
如果您的项目中没有 .eslintrc.js 文件,您可以按以下步骤创建并配置 ESLint: 1. 创建 ESLint 配置文件 在您的项目根目录下创建一个新的文件,命名为 .eslintrc.js。 2. 配置 ESLint 规则 在 .eslintrc.js 文件中添加以下内容,…...

确保企业架构与业务的一致性与合规性:数字化转型中的关键要素与战略实施
在现代企业的数字化转型过程中,确保企业架构(Enterprise Architecture, EA)与企业业务的紧密一致性与合规性至关重要。无论是在战略层面还是运营层面,EA都为企业的未来发展提供了清晰的蓝图,确保企业在应对复杂的业务环…...

goframe开发一个企业网站 前端界面 拆分界面7
将页面拆出几个公用部分 在resource/template/front创建meta.html header.html footer.html meta.html <head><meta charset"utf-8"><meta content"widthdevice-width, initial-scale1.0" name"viewport"><title>{{.…...

Postman断言与依赖接口测试详解!
在接口测试中,断言是不可或缺的一环。它不仅能够自动判断业务逻辑的正确性,还能确保接口的实际功能实现符合预期。Postman作为一款强大的接口测试工具,不仅支持发送HTTP请求和接收响应,还提供了丰富的断言功能,帮助测试…...

github打不开网络问题
当打开github出现超时或者网络不能访问的情况时,我们进行如下方法解决: 1,ping gitbub.com查看域名分析的DNS IP C:\Users\86156>ping github.com 正在 Ping github.com [20.205.243.166] 具有 32 字节的数据: 来自 20.205.243.166 的回复…...

智能教育工具:基于SpringBoot的在线试题库
1 绪论 1.1 研究背景 现在大家正处于互联网加的时代,这个时代它就是一个信息内容无比丰富,信息处理与管理变得越加高效的网络化的时代,这个时代让大家的生活不仅变得更加地便利化,也让时间变得更加地宝贵化,因为每天的…...

typescript 如何跳过ts类型检查?
文章目录 前言any类型条件判断进行使用断言加注释跳过ts检查 前言 typescript 的使用,虽然让代码更加规范,利于维护,但也给开发带来很多麻烦。为了跳过很多ts的类型检查,大家也是费尽心思,下面就介绍一些常用的方式&a…...

详解ReentrantLock--三种加锁方式
目录 介绍AQS: 直观方式解释加锁的流程: Node是什么:它里面有什么属性呢 图解队列的排队过程: 源码分析三种加锁流程: 我们先讲解一下非公平锁的加锁流程: Lock()方式加锁: 在源码里对于Lock()的解…...

SQL 基础语法(一)
文章目录 1. SQL 分类2. 数据库操作3. 数据表操作4. 增删改操作5. 查询操作6. 用户管理7. 权限控制 1. SQL 分类 2. 数据库操作 #创建数据库 create database if not exists test;#查询所有数据库 show databases;#查询当前数据库 select database();#删除数据库 drop databas…...

Python酷库之旅-第三方库Pandas(190)
目录 一、用法精讲 881、pandas.Index.is_方法 881-1、语法 881-2、参数 881-3、功能 881-4、返回值 881-5、说明 881-6、用法 881-6-1、数据准备 881-6-2、代码示例 881-6-3、结果输出 882、pandas.Index.min方法 882-1、语法 882-2、参数 882-3、功能 882-4、…...

Spring学习笔记_19——@PostConstruct @PreDestroy
PostConstruct && PreDestroy 1. 介绍 PostConstruct注解与PreDestroy注解都是JSR250规范中提供的注解。 PostConstruct注解标注的方法可以在创建Bean后在为属性赋值后,初始化Bean之前执行。 PreDestroy注解标注的方法可以在Bean销毁之前执行。 2. 依赖…...

《云计算网络技术与应用》实训8-1:OpenvSwitch简单配置练习
1.按《云计算网络技术与应用》实训5-1进行环境配置,安装好OVS 2.开启OVS虚拟交换机 3.创建一个网桥br0 4.查看网桥列表 5.把ens34网卡连接到网桥br0上 6. 查看网桥br0所有端口 7.列出网卡ens34连接的所有网桥列表 8.查看OVS网络状态 9.将网桥br0上连接的网卡ens34删…...

【架构艺术】服务架构稳定性的基础保障
一个产品随着不断研发,其服务架构的复杂度会越来越高。随着产品的用户体量变大,为了保证产品能够长线运营,就需要保证整个服务架构的稳定性。因此,今天这篇文章,就从实操的角度,粗浅讨论一下,服…...

Python中使用pip换源的详细指南
在Python开发过程中,我们经常需要安装各种第三方库。pip是Python的包管理工具,用于安装和管理Python库。然而,由于网络原因,有时访问默认的Python包索引(PyPI)可能会比较慢。这时,我们可以通过更…...
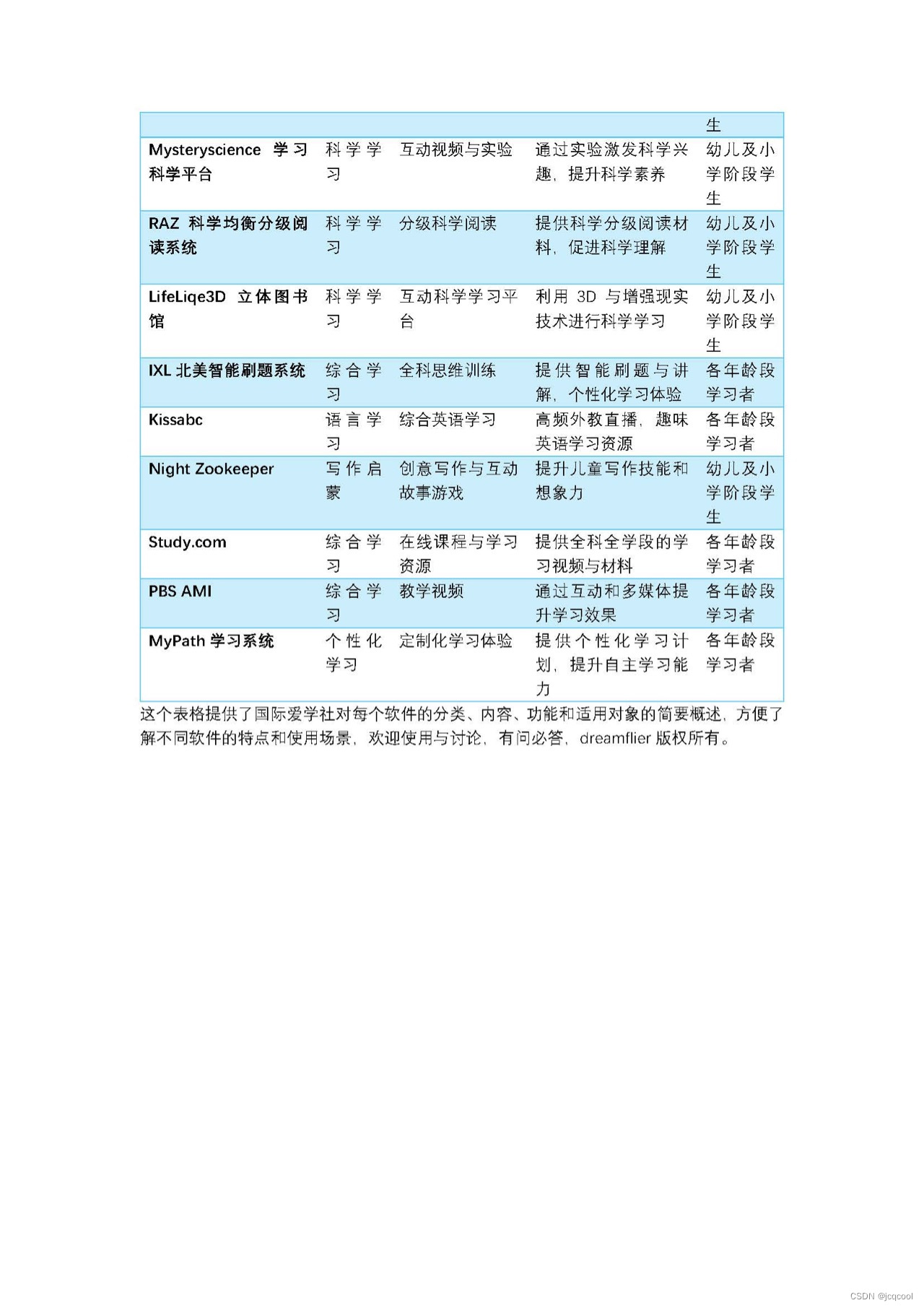
一站打包国际智慧教育自主学练软件资源
👑🌟一站打包国际智慧教育自主学练软件与资源平台,欧美学校正在使用,不出国就可以学👒🎈 💛 多元学练:我们正在使用的自主学练软件是美国学校一线教师使用的,涵盖了英语…...

用股票API获取高频行情数据来实现数据分析和量化
用股市API获取高频行情来实现数据分析和量化 使用股市API是一种有效的方式来获取高频行情数据,以便进行行情数据分析和量化交易。Python是一种广泛应用于金融数据领域的编程语言,它提供了丰富的库和工具,可用于与股市API进行交互。通过调用股…...

C++ | Leetcode C++题解之第526题优美的排列
题目: 题解: class Solution { public:int countArrangement(int n) {vector<int> f(1 << n);f[0] 1;for (int mask 1; mask < (1 << n); mask) {int num __builtin_popcount(mask);for (int i 0; i < n; i) {if (mask &am…...

【RabbitMQ】01-RabbitMQ
1. MQ MQ可以有更好的并发性。 2. 安装 docker run \-e RABBITMQ_DEFAULT_USERitheima \-e RABBITMQ_DEFAULT_PASS123321 \-v mq-plugins:/plugins \--name mq \--hostname mq \-p 15672:15672 \-p 5672:5672 \--network hm-net\-d \rabbitmq:3.8-management3. 结构 4. 数据…...
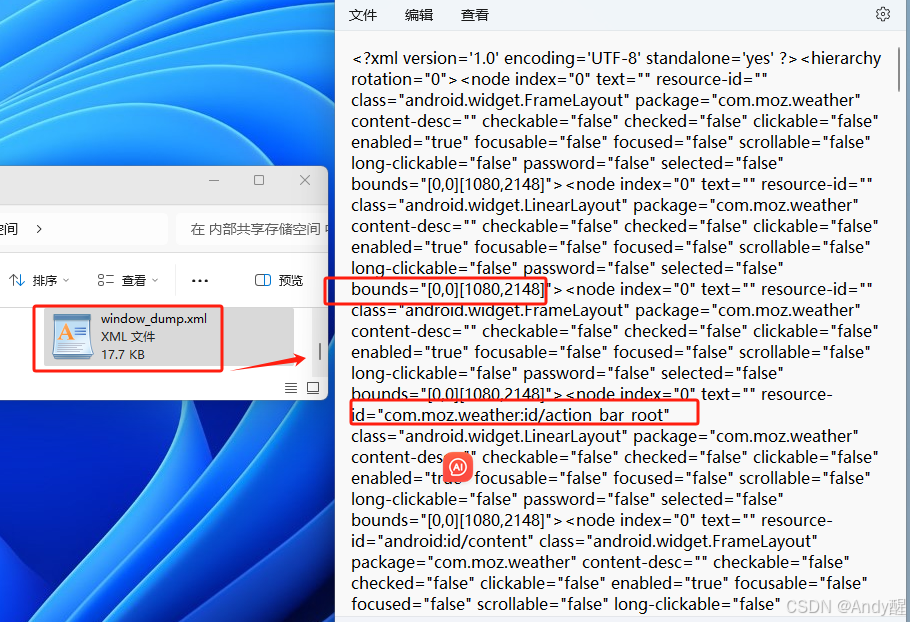
使用 ADB 在某个特定时间点点击 Android 设备上的某个按钮
前提条件 安装 ADB:确保你已经在计算机上安装了 Android SDK(或单独的 ADB)。并将其添加到系统环境变量中,以便你可以在命令行中运行 adb。 USB调试:确保 Android 设备已启用 USB 调试模式。这可以在设备的“设置” -…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...
