牛客题目解析
一.最长回文子串
1.题目:给定一个仅包含小写字母的字符串,求它的最长回文子串的长度。
最长回文子串__牛客网
2.算法原理:
<1>动态规划算法:O(n^2),O(n^2) 具有通性,凡涉及回文子串的问题都可利用此法解决
知识储备:对与只有一个字符的字符串一定是回文串;对于有两个字符的字符串当两个字符相等时,才是回文串;当字符串的长度大于2时,若该字符串是回文串则去掉首尾两个字符后仍是回文串。
创建一个n*n的dp表,统计[i,j]区间段内的子串是否是回文串。当i<j时,dp[i][j]=0;当i==j时,dp[i][j]==1;当j-i==1时,判断str[i]和str[j]是否相等;当j-i>1时,若str[i]==str[j],则判断dp[i+1][j-1]是否为1,若str[i]!=str[j],则dp[i][j]=0
注意:要是按照常规思维,利用字符串的长度两次循环的话,会出现判断dp[3][6]需要去看dp[4][5]的情形,而dp[4][5]还没有进行计算的情况,所以我们可以利用首尾字符间的距离作为第一层循环的自变量,从而避免访问还未判断位置的信息的情况
int getLongestPalindrome(string A) {int n=A.size();vector<vector<int>> r(n,vector<int>(n));int back;//创建矩阵在r中保存当前r[i][j]是否是回文子串,判定的依据为r[i+1][j-1]==1且A[i]==A[j]for(int d=0;d<n;d++)//d:两者间的间距{for(int i=0;i<n-d;i++){int j=i+d;if(d==0)r[i][j]=1;else if(d==1)r[i][j]=(A[i]==A[j]);elser[i][j]=(A[i]==A[j]&&r[i+1][j-1]==1);if(r[i][j]&&d+1>ret.size()){back=j-i+1;}}}return back;<2>马拉车算法:O(n),O(n) 不具有通性,只能用于解决这一种问题
此种算法思想小编暂时还没有掌握,后续若是掌握了会在评论区介绍的,有兴趣的宝子可以自己尝试理解,要是学会了记得教小编一下
<3>中心扩展算法:O(n^2),O(1)
遍历字符串,以拿到的字符str[i]为回文子串的中心字符,然后利用两个指针left和right以str[i]为中心,分别向左右扩展,直至不符合str[left]!=str[right],更新回文子串的最长长度。
注意:因为回文子串的长度可以是奇数也可以是偶数,所以对于初始时left的赋值应该考虑left=i,和left=i-1两种情况
#include <iostream>
#include<string>
using namespace std;int main() {string str;cin>>str;//中心扩展算法int left=0,right=0,ret=0;for(int i=0;i<str.size();i++){//长度为奇数的回文串left=i-1;right=i+1;while(left>=0 && right<str.size() && str[left]==str[right]){left--;right++;}ret=max(ret,right-left-1);//长度为偶数的回文串left=i;right=i+1;while(left>=0 && right<str.size() && str[left]==str[right]){left--;right++;}ret=max(ret,right-left-1);}cout<<ret<<endl;return 0;
}二.游游的水果大礼包(二元一次方程组的求解问题)
1.题目: 游游的水果大礼包__牛客网
游游有n个苹果,m个桃子。她可以把2个苹果和1个桃子组成价值a元的一号水果大礼包,也可以把1个苹果和2个桃子组成价值b元的二号水果大礼包。游游想知道,自己最多能组成多少价值总和的大礼包?
2.算法原理:
利用枚举法从0开始假设可以组成x个1号大礼包,x的取值范围为[0,min(n/2,m)],定下来1号礼包的个数,那么可以计算出2号礼包的个数,y=min(n-2*x,(m-x)/2),则礼包总值为a*x+b*y,在枚举过程中更新总值的最大值
3.代码实现:
#include <iostream>
using namespace std;int main() {long long n,m,a,b;cin>>n>>m>>a>>b;long long ret=0;for(long long x=0;x<=min(n/2,m);x++)//枚举1号礼包个数{long long y=min((n-2*x),(m-x)/2);//计算2号礼包个数ret=max(ret,a*x+b*y);}cout<<ret<<endl;return 0;
}
注:有些题目的数字类型要特别注意,否则可能会让测试结果就卡在70%左右非常恶心,建议对于可能取大值的数据一律定义long long类型,一了百了
三.两个链表的第一个公共节点
1.题目:两个链表的第一个公共结点_牛客题霸_牛客网
输入两个无环的单向链表,找出它们的第一个公共结点,如果没有公共节点则返回空。
2.算法原理:
<1>常规思路:统计出两个链表的长度,让长的链表先走两链表差值步,再和另一链表开始一起向后走,当第一次碰到相同的节点时,则该节点就是第一个公共节点
注意:有可能在长链表走链表差步时,就已经达到第一个公共节点处,此情况不要忘记考虑
<2>等量关系:让cur1,cur2分别指向两链表的头节点,当cur1走到空时,让cur1指向另一个链表的头节点;同理,当cur2走到空时,让cur2指向另一个链表的头节点,让cur1==cur2时,所指向的节点就是第一个公共节点。

class Solution {
public:ListNode* FindFirstCommonNode( ListNode* pHead1, ListNode* pHead2) {if(pHead1==nullptr || pHead2==nullptr) return nullptr;ListNode* cur1=pHead1;ListNode* cur2=pHead2;while(cur1!=cur2){cur1=cur1==nullptr?pHead2:cur1->next;cur2=cur2==nullptr?pHead1:cur2->next;}return cur1;}
};小小感慨一下,果然普通人是比不上天才的,这种思路绝对不是我这种普通人能想出来的🥲
四.Mari和shiny(多状态的动态规划问题)
1.题目:在一个字符串中找出"shy"的子序列
注:子串和子序列是不一样的,子串要求在原字符串中连续出现,但是子序列不要求连续出现,吐槽一句真恶心
2.算法原理:
利用数组统计在该字符前有多少个满足条件的选项。
创建shy数组统计该字符前有多少个“sh",若是str[i]=='y',则shy[i]=shy[i-1]+sh[i];若不等,则shy[i]=shy[i-1]
创建sh数组统计该字符前有多少个“s",若是str[i]=='h',则sh[i]=sh[i-1]+s[i];若不等,则sh[i]=sh[i-1]
创建s数组统计该字符前有多少个“s",若是str[i]=='s‘,则s[i]=s[i-1]+1;若不等,则s[i]=s[i-1]
注:可对本题做空间优化,即不创建数组直接利用三个变量统计
若str[i]=='s',则s++;若str[i]=='h',则h+=s;若str[i]=='y',则y+=h;
3.代码实现:
#include<iostream>
#include<string>
using namespace std;int main()
{string str;cin >> str;int s = 0, h = 0, y = 0;for (int i = 0; i < str.size(); i++){if (str[i] == 's') s++;else if (str[i] == 'h') h += s;else if (str[i] == 'y') y += h;}cout << y << endl;return 0;
}zhu
相关文章:

牛客题目解析
一.最长回文子串 1.题目:给定一个仅包含小写字母的字符串,求它的最长回文子串的长度。 最长回文子串__牛客网 2.算法原理: <1>动态规划算法:O(n^2),O(n^2) 具有通性,凡涉及回文子串的问题都可利用此法解决 知识储备&am…...

AG32的3个ADC可以并联使用吗
AG32的3个ADC可以并联使用吗? Customer: 需求: 在t1时间段,用5M的速度ch1通道采样得到结果1. 在t2时间段,用5M的速度ch2通道采样得到结果2. 在t3时间段,用5M的速度ch3通道采样得到结果3. 然后如此循环 。 考虑用3…...

什么是 OpenTelemetry?
OpenTelemetry 定义 OpenTelemetry (OTel) 是一个开源可观测性框架,允许开发团队以单一、统一的格式生成、处理和传输遥测数据(telemetry data)。它由云原生计算基金会 (CNCF) 开发,旨在提供标准化协议和工具,用于收集…...

[vulnhub]DC:7
https://www.vulnhub.com/entry/dc-7,356/ 端口扫描主机发现 探测存活主机,178是靶机 nmap -sP 192.168.75.0/24 Starting Nmap 7.94SVN ( https://nmap.org ) at 2024-11-03 13:30 CST Nmap scan report for 192.168.75.1 Host is up (0.00037s l…...

个性化十足的贵族服务器,惠普ML310e Gen8,服务器中的 “潘多拉魔盒”
个性化十足的贵族服务器,惠普ML310e Gen8,服务器中的 “潘多拉魔盒” 小伙伴们大家好呀,这里是勤奋的凯尔森同学,今天给大家分享一款好玩的服务器,惠普ML310e Gen8 V2,相比大家都很熟悉HP ProLiant MicroS…...

百度社招内推
百度社招内推 「百度内推」快来投递你心仪的职位吧( 网申链接地址:https://dwz.cn/ah4OUcca),填入内推码,完成投递,get内推绿色通道~我的内推码:IZ9PVH 内推有什么好处: 简历直达…...
本地部署开源在线即时通讯软件Fiora打造个人私密聊天室
文章目录 前言1.关于Fiora2.安装Docker3.本地部署Fiora4.使用Fiora5.cpolar内网穿透工具安装6.创建远程连接公网地址7.固定Uptime Kuma公网地址 前言 相信大家在聊天时候总是很没安全感,比如在和小姐妹背着男朋友聊一些不能说的坏话,或者背着女朋友和兄…...

TS(类 接口 泛型)
文章目录 类复习相关知识属性修饰符public 修饰符属性的简写形式 protected修饰符private修饰符readonly修饰符 抽象类 接口(interface)定义类结构定义对象结构定义函数结构接口之间的继承接口自动合并 (可重复定义)一些相似的概念…...

docker 启动 neo4j
docker 启动 neo4j 1. 启动2. 导入数据 1. 启动 运行下面命令启动 neo4j, docker run \-d \--restartalways \--publish7474:7474 --publish7687:7687 \--volume$HOME/neo4j-4.4.38/data:/data \--name neo4j-apoc-4.4.38 \-e NEO4J_dbms_allow__upgradetrue \-e …...
OPENAI官方prompt文档解析
官方文档地址:https://platform.openai.com/docs/guides/gpt-best-practices 文档中文版来源:OpenAI 官方提示工程指南 [译] | 宝玉的分享 (baoyu.io) 1.写清楚说明 如果prompt给的范围十分模糊或是过于宽泛,那么GPT就会开始猜测您想要的内容,从而导致生成的结果偏离预期. …...
【GESP】C++一级练习BCQM3092,双面打印
GESP一级知识点if分支语句和取余、整除操作练习。比较简单。 题目题解详见:https://www.coderli.com/gesp-1-bcqm3092/ 【GESP】C一级练习BCQM3092,双面打印 | OneCoderGESP一级知识点if分支语句和取余、整除操作练习。比较简单。https://www.coderli.…...

mysql--多表查询
一、联合查询 作用:合并结果集就是把两个select语句的查询结果合并到一起! 合并结果集有两种方式: UNION:合并并去除重复记录,例如:SELECT * FROM t1 UNION SELECT * FROM t2; UNION ALL&a…...

RHCE-Web-nginx http实验和nginx https实验
一、web服务器简介 (1)什么是www www 是 world wide web 的缩写,也就是全球信息广播的意思。通常说的上网就是使用 www 来查询用户 所需要的信息。 www 可以结合文字、图形、影像以及声音等多媒体,并通过可以让鼠标单击超链接的…...

少儿编程学习现状洞察:青少年编程教育需求与学习频率分析
随着少儿编程教育的逐渐普及,越来越多的家庭开始关注孩子在编程学习中的表现。根据最新数据,90%的少儿编程学员保持每周至少一节课的学习频率,而95%的编程课程都安排在周末。特别是在8岁、10岁、12岁及15岁以上的年龄层次,孩子的学…...

接口集成、快速对接-阿里身份证实名认证接口
身份证实名认证接口现已被应用在联网的各种业务场景中,如电商、在线教育、银行等等,下面以电商平台为例,列举翔云身份证实名认证接口在电商平台中的具体应用和优势。 电商平台的出现方便了人们的生活,进行电商的实名认证有助于提高…...

HTTP、WebSocket、gRPC 或 WebRTC:各种协议的区别
在为您的应用程序选择通信协议时,有很多不同的选择。 本文将了解四种流行的解决方案:HTTP、WebSocket、gRPC 和 WebRTC。 我们将通过深入学习其背后原理、最佳用途及其优缺点来探索每个协议。 通信方式在不断改进:变得更快、更方便、更可靠&…...

Unity3D学习FPS游戏(8)装弹和弹夹UI显示
前言:实现了武器的基本发射功能,但是我们弹夹数量是有限,之前并没有做装弹和弹夹显示的功能。本篇实现装弹和弹夹显示。 装弹和弹夹UI显示 装弹目标思路和实现 弹夹UI显示目标弹夹UI的思路和实现UI代码的思路和实现 武器控制的完整代码效果补…...
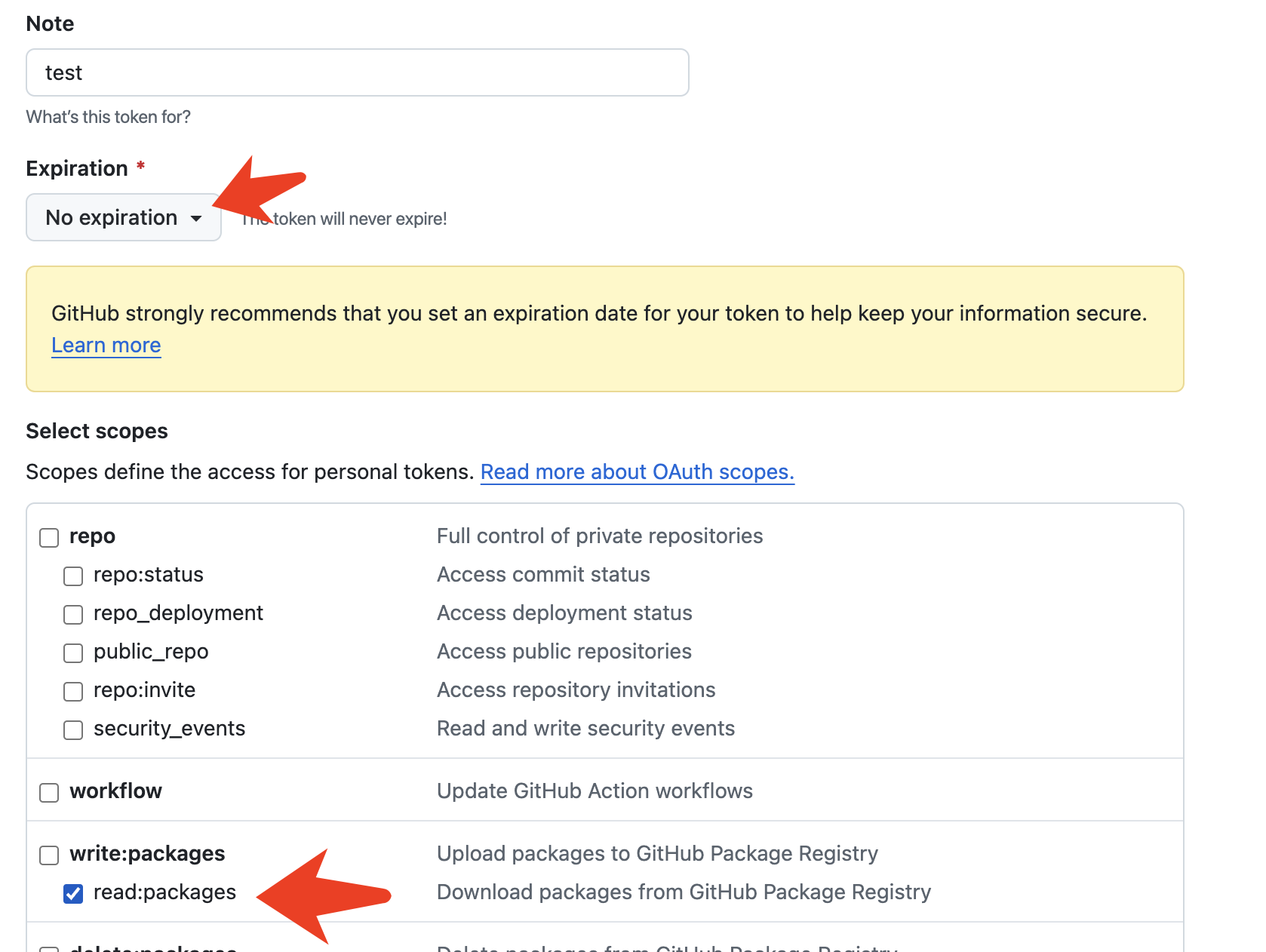
Android 托管 Github Action 发布 Github Packages ,实现 Mvn 免费自动化托管
自从多年前 JCenter 关闭服务之后,GSY 项目版本就一直发布在 Jitpack 上,如今每个月也都有大概 10w 左右下载,但是近年来时不时就会出现历史版本丢失的问题,而且有时候还不是某个具体版本丢失,而是版本里的某几个依赖突…...
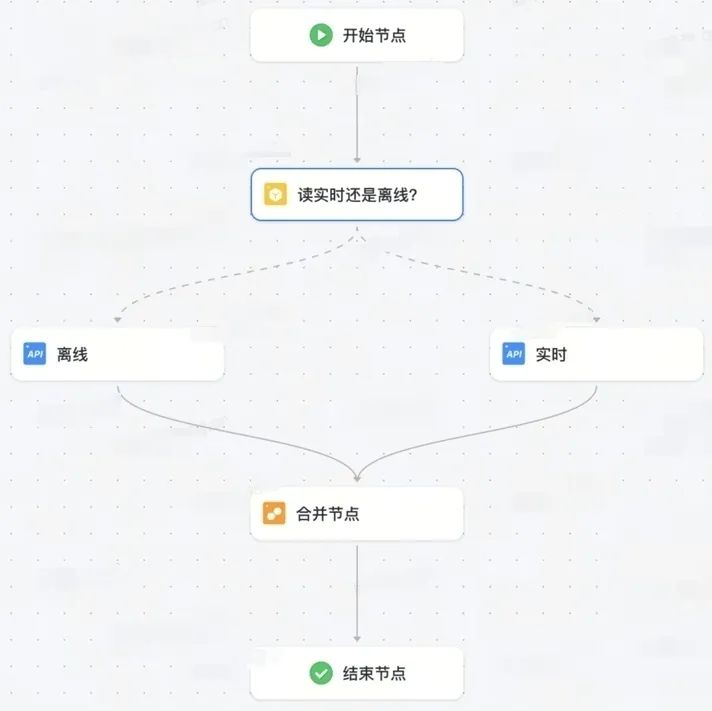
火山引擎VeDI数据服务平台:在电商场景中,如何解决API编排问题?
01 平台介绍 数据服务平台可以在保证服务高可靠性和高安全性的同时,为各业务线搭建数据服务统一出口,促进数据共享,为数据和应用之间建立了一座“沟通桥梁”。 同时,解决数据理解困难、异构、重复建设、审计运维困难等问题&#x…...

【每日C/C++问题】
一、 结构体和联合体有什么区别?能否在声明过程当中缺省名字?(需要写清楚使用方法) 结构体的各个成员占用不同的内存空间,总大小是所有成员大小之和(结构体字节对齐): typedef str…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...
