分数阶傅里叶变换与信息熵怎么用于信号处理？

天马行空的理解与思考方式：分数阶傅里叶变换与信息熵怎么用于信号处理？

ChiX-Y

快速学习，快速尝试，快速失败

已关注

35 人赞同了该文章

这篇文章希望能写的有趣，同时有质量，学习就是要多维度多角度！

信息熵怎么用于各类信号处理？（信号特征提取？信号识别与分类？）

一.什么是信息熵？

热力学中的热熵是表示分子状态混乱程度的物理量，而信息熵的概念是用来描述信源的不确定度的；信息论之父香农曾在论文中提出“任何信息都存在冗余，冗余大小与信息中每个符号（数字、字母或单词）的出现概率或者说不确定性有关。”香农借助热力学概念，把信息中排除了冗余后的平均信息量称为“信息熵”。

通常，一个信源发送出什么符号是不确定的，衡量它可以根据其出现的概率来度量。出现的概率大，则不确定性小，所提供的信息量就少；反之不确定性就大。

根据以上定义和描述，可以得到不确定性函数应具有的两个条件：

①不确定性函数 f 是概率 p 的减函数；②两个独立符号所产生的不确定性应等于各自不确定性之和，即 f(p1,p2)=f(p1)+f(p2) ,这是不确定性函数的可加性。

同时满足以上两个条件的函数 f 是对数函数，即 f(p)=log1p=−log(p)

在信源中，考虑的不是某一单个符号发生的不确定性，而是要考虑这个信源所有可能发生情况的平均不确定性。若某个信源可以出现n种符号来传递信息： U1...Ui...Un ，对应的概率为： p1...pi...pn ，且各种符号的出现彼此独立。这时，信源的平均不确定性应当为单个符号不确定性 −log(pi) 的统计平均值（E），称为信息熵，即 H(U)=E[−log(pi)]=−∑i=1npilog(pi)

上式中的对数一般取2为底，单位为比特。

离散的信源信息熵具有：①非负性 ②对称性 ③确定性 ④极值性

二.分数阶傅里叶变换

为了能让信息熵更好的在信号处理中派上用场，需要先学习一种更高级的信号处理数学工具

分数阶傅里叶变换

---

这里真的很想吐槽一下，网上关于分数阶傅里叶变换的学习资料真的是蛮少的，很多“大佬”对于这个数学方法的描述就是列出来一大堆复杂而又难懂的数学公式，看懂了数学公式，理清了推导过程也只是“知其然，而不知其所以然”，所以承担着掉几根头发的代价...我想到了一种以图像来理解分数阶傅里叶变换本质思想的方法，这将有助于后续的信号处理应用。当然，如果有数学系大佬指出其中理解不妥的地方，那真的非常感激！

---

我们不着急从这个复杂的数学方法入手，作为一个基本的工科生，我们一定是学过傅里叶变换的，如果你在平日的学习中习惯于思考，那么你一定会记得傅里叶变换就是在“帮助我们换个角度看世界”。

“世界变化无常，可换个角度，或许只是已经写好的乐章。”

傅爷爷告诉我们，任何周期函数（非周期函数需要无数个），都可以由许多不同振幅，不同相位的正弦波叠加而来。我们看一下下面这一张来自维基百科的图。

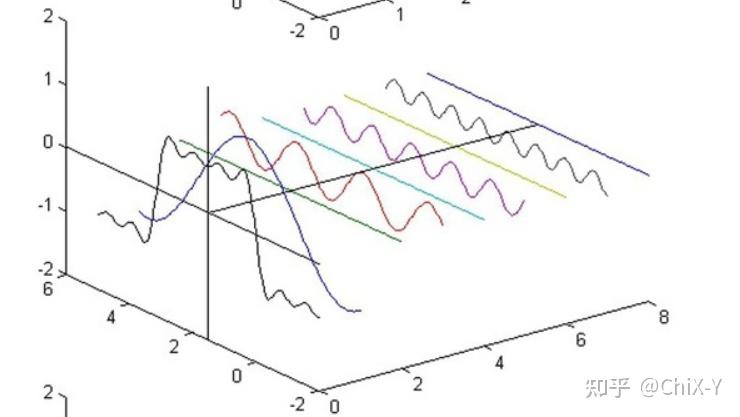
最前面那条黑色的函数曲线（矩形波），可以由后面多条正弦曲线叠加而成，这些依不同颜色排列而成的正弦曲线就是组合成为矩形波的各个频率分量。细心的你可能发现中间有一些直线，这些直线是振幅为0的正弦曲线，这就说明为了组成不同的曲线，有些频率成分是不需要的！

OK，既然我们已经回忆了一般的傅里叶变换做了什么事情，那我们接下来就可以想一下，一条时间维度上的信号曲线到底换了怎么样的角度而到了我们想要频域空间呢？？必须要天马行空的想想，这对于帮助我们理解分数阶傅里叶变换有着至关重要的作用！

我们看下面这张图：

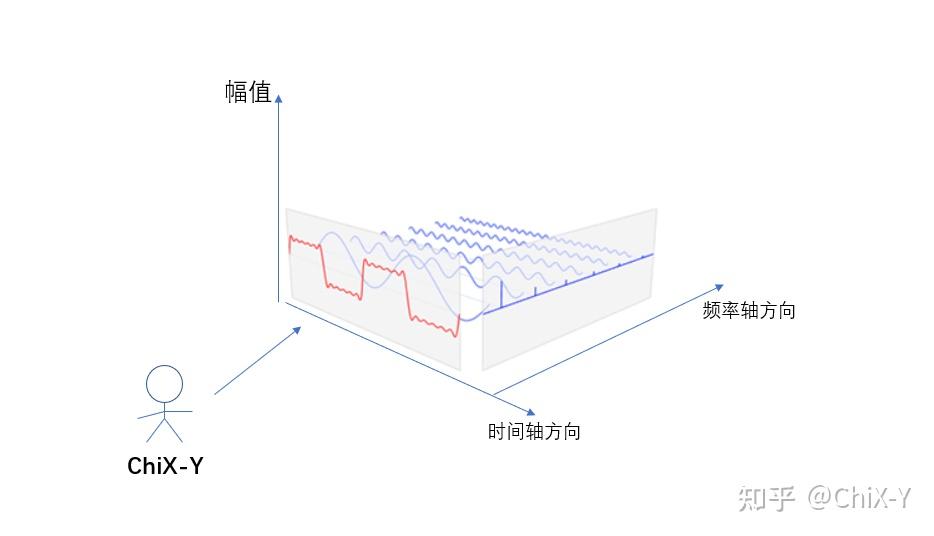
一开始，我（ChiX-Y）站在垂直时间轴而平行于频率轴的方向，这个时候我看到的就是那一条红色的曲线（它由后面许多不同频率成分的正弦波叠加而成），从这个角度看到的红色曲线其实就是时间域上的信号曲线了，ok，那么我要换什么角度才能够看到频域世界里这条曲线的模样呢？我想你们一定已经想到了，对，就是逆时针旋转90°以后，从侧面方向来看这一天红色曲线！！！（如下图）

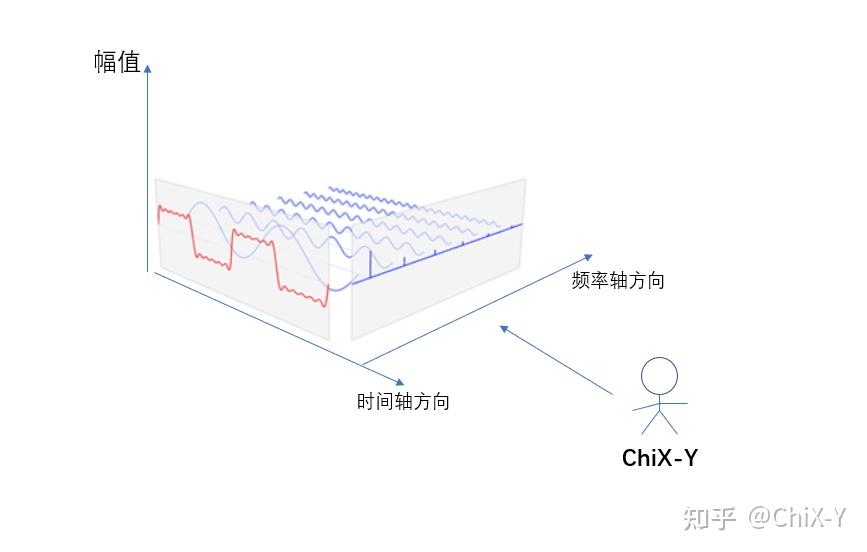
我走到上图中的这个角度以后，我看到各个频率成分的正弦曲线就是一条条平行于Z轴的竖线，而此时的横轴是频率轴，怎么样？熟悉吗？这不就是我们一直以来求的频谱吗！！！

所以我们完全可以这么去解释傅里叶变换：信号的Fourier变换可以看成将其在时间轴上逆时针旋转 π/2到频率轴上的！换句好理解的话来讲，信号的Fourier变换就是从时间轴角度转了90°到频率轴上来看到的新世界！

OK，既然我想到了以这么一种立体而又形象的角度去看待傅里叶变换，那么接下来的分数阶傅里叶变换就容易解释了！

所谓的分数阶傅里叶变换就是换更多的角度去看待问题，怎么解释？

就是我在从初始位置走向90°方位的时候，并不是一次性的就走过去了，而是每走一定的角度就停下来看一看我们在当前角度下能够看到红色信号曲线的什么特征与特性，并记录每个角度下“频率域”的频谱，这么做是因为大部分的信号都是非平稳信号，仅仅用傅里叶变换不足以分析其显著的特征，运用分数阶傅里叶变换主要是能选取信息最集中的角度去分析。

大家想想，分析问题的角度越多，是不是解决问题的方法就越完善呢？

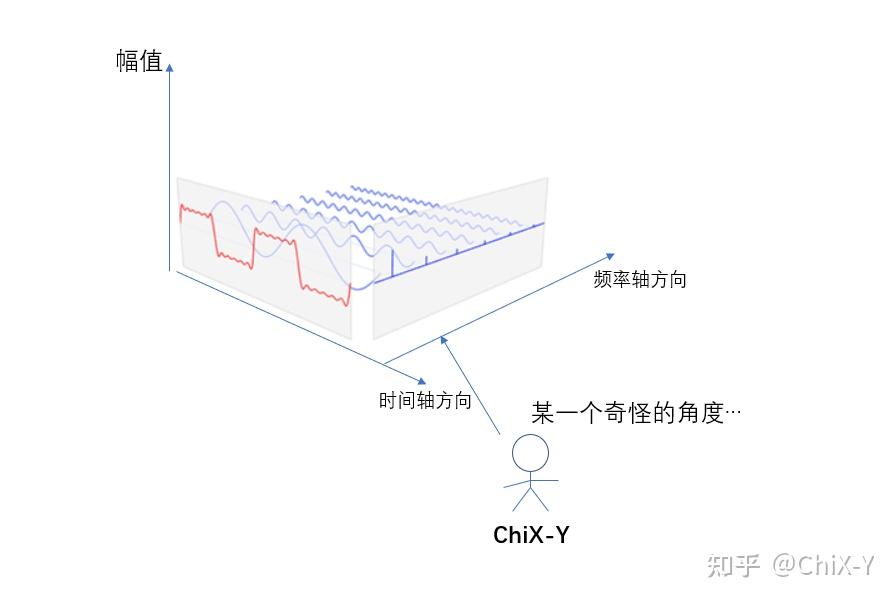
到这里我希望大家是能够理解了我分析这个数学方法的角度，也希望各位能够从复杂的数学公式中跳脱出来，真正理解了分数阶傅里叶变换到底做了什么事情，做到了这一点，让我想到了利用信息熵来做信号处理的一种思路！

三.信息熵+分数阶傅里叶变换->信号处理

如果理解了前文我所写的全部内容，那么接下来这个信号处理的思路就真的很简单了，算是自己的一些想法吧，我拿心电信号来举例子：

（1）采集一段心电信号并做预处理，获得信号d

（2）对信号d进行n个阶次（n个角度，大家懂的！）的分数阶傅里叶变换，从而进一步得到每一个阶次变换的幅度谱 Fi

（3）对幅度谱 Fi归一化后，计算每一个幅度谱的信息熵，n个阶次对应n个信息熵，从而得到一个n点长的向量[E1,...,Ei,...,En]，这个向量就可以作为心电信号所提取的特征，然后进一步用于算法的学习与信号分类。

这样的思路我认为有两个优势：第一是从更多的角度去提取信号的特征，使得信号特征更为丰富与全面，能够提升对信号分类与识别准确率；第二是利用信息熵有效缓解了角度过而导致的特征过于复杂的问题，因为一个角度的信息熵只有一个值哦！

四.有趣的感悟

我们眼中的世界就像是一条条时域中的曲线，变换多端，毫无规律，难以预测......但或许真的存在一种角度，能够看到其实我们的世界真的没有那么复杂，它只是一场已经安排好的音乐会，每一个音符都已经注定会出现，就像是频谱中一条条平行于Z轴的直线，简单清晰。

编辑于 2021-08-13 12:25