【数据结构二叉树】C非递归算法实现二叉树的先序、中序、后序遍历
引言:
遍历二叉树:指按某条搜索路径巡访二叉树中每个结点,使得每个结点均被访问一次,而且仅被访问一次。
除了层次遍历外,二叉树有三个重要的遍历方法:先序遍历、中序遍历、后序遍历。
1、递归算法实现先序、中序、后序遍历:
(1)先序遍历:
void PreOrderTraverse(BiTree T)
{if(T){cout<<T->data;PreOrderTraverse(T->lchild);PreOrderTraverse(T->rchild);}
}
(2)中序遍历:
void InOrderTraverse(BiTree T)
{ if(T){InOrderTraverse(T->lchild);cout<<T->data;InOrderTraverse(T->rchild);}
} (3)后序遍历
void PostOrderTraverse(BiTree T)
{ if(T){ PostOrderTraverse(T->lchild); PostOrderTraverse(T->rchild); cout<<T->data; }
}
2.非递归算法实现先序、中序、后序遍历:
采用非递归算法则需要利用栈来实现对二叉树的遍历:
(1)先序遍历非递归算法
void PreOrder_non_recursion(BiTree T)//先序遍历的非递归算法
{LinkStack S;InitStack (S); BiTree p,q;p=T;while(p||!StackEmpty(S)){if(p){Push(S,*p); cout<<p->data; //访问根节点 p=p->lchild; //遍历左子树 }else{Pop(S,*q);p=q->rchild; //遍历右子树 }}
}
(2)中序遍历非递归算法
void InOrder_non_recursion(BiTree T)//中序遍历的非递归算法
{LinkStack S;InitStack (S); BiTree p; BiTree q; p=T;while(p||!StackEmpty(S)){if(p){Push(S,*p); p=p->lchild; //遍历左子树 }else{Pop(S,*q);cout<<q->data; //访问根节点 p=q->rchild; //遍历右子树 }}
}
(3)后序遍历非递归算法
(采用非递归算法实现对二叉树的后序遍历,会稍微复杂一些,本算法借用了两个栈结构)
void PostOrder_non_recursion(BiTree T)//后序遍历的非递归算法
{LinkStack l_S,r_S;InitStack (l_S);InitStack (r_S);BiTree p,q; p=T;Push(l_S,*p);while(!StackEmpty(l_S)){Pop(l_S, *q);Push(r_S,*q);if(q->lchild){Push(l_S, *q->lchild);}if(q->rchild){Push(l_S,*q->rchild);}}while(!StackEmpty(r_S)){Pop(r_S,*q);cout<<q->data;}
}
3.完整代码
1、采用按照先序遍历的顺序建立二叉链表,用‘#’表示空树。如图所示:

2、先序遍历的递归与非递归算法的对比:
#include<iostream>
#define OK 1
#define ERROR 0
#define OVERFLOW -2
using namespace std;
typedef char TElemType;
typedef int Status;typedef struct BiTNode{ //二叉树的存储结构TElemType data; // 数据域struct BiTNode *lchild; //左孩子指针struct BiTNode *rchild; //右孩子指针
}BiTNode, *BiTree;typedef struct StackNode { //栈的存储结构BiTNode data; //栈数据元素类型为树结点型 struct StackNode *next;
} StackNode, *LinkStack;Status InitStack(LinkStack &S) { //栈初始化S = NULL;return OK;
}Status Push(LinkStack &S, BiTNode e) { //入栈LinkStack p;p = new StackNode; //生成新结点if (!p) {return OVERFLOW;}p->data = e; //将新结点数据域置为ep->next = S; //将新结点插入栈顶S = p; //修改栈顶指针为preturn OK;
}Status Pop(LinkStack &S, BiTNode &e) { //出栈LinkStack p;if (S == NULL)return ERROR; //栈空e = S->data; //将栈顶元素赋给ep = S; //用p临时保存栈顶元素空间,以备释放S = S->next; //修改栈顶指针delete p; //释放原栈顶元素的空间return OK;
}bool StackEmpty(LinkStack S) { //判断是否空栈if (!S)return true;return false;
}void CreateBiTree_PreOrder(BiTree &T){ //以先序次序创建二叉树 char ch; cin>>ch;if(ch=='#')T=NULL; else{T=new BiTNode; //生成根结点T->data=ch; //根结点的数据域置为chCreateBiTree_PreOrder(T->lchild);//构造左子树CreateBiTree_PreOrder(T->rchild); //构造右子树}}void PreOrder(BiTree T){ //先序遍历的递归递归算法if(T){cout<<T->data;PreOrder(T->lchild);PreOrder(T->rchild);}
}void PreOrder_non_recursion(BiTree T)//先序遍历的非递归算法
{LinkStack S;InitStack (S); BiTree p,q;p=T;while(p||!StackEmpty(S)){if(p){Push(S,*p); cout<<p->data; //访问根节点 p=p->lchild; //遍历左子树 }else{Pop(S,*q);p=q->rchild; //遍历右子树 }}
}int main() {BiTree T;cout<<"以先序次序创建二叉链表,以#表示空子树:"<<endl;CreateBiTree_PreOrder(T);cout<<"先序序列(递归算法):"; PreOrder(T); cout<<"\n先序序列(非递归算法):"; PreOrder_non_recursion(T);return 0;
}实验结果:

3、中序遍历的递归与非递归算法的对比:
#include<iostream>
#define OK 1
#define ERROR 0
#define OVERFLOW -2
using namespace std;
typedef char TElemType;
typedef int Status;typedef struct BiTNode{ //二叉树的存储结构TElemType data; // 数据域struct BiTNode *lchild; //左孩子指针struct BiTNode *rchild; //右孩子指针
}BiTNode, *BiTree;typedef struct StackNode { //栈的存储结构BiTNode data; //栈数据元素类型为树结点型 struct StackNode *next;
} StackNode, *LinkStack;Status InitStack(LinkStack &S) { //栈初始化S = NULL;return OK;
}Status Push(LinkStack &S, BiTNode e) { //入栈LinkStack p;p = new StackNode; //生成新结点if (!p) {return OVERFLOW;}p->data = e; //将新结点数据域置为ep->next = S; //将新结点插入栈顶S = p; //修改栈顶指针为preturn OK;
}Status Pop(LinkStack &S, BiTNode &e) { //出栈LinkStack p;if (S == NULL)return ERROR; //栈空e = S->data; //将栈顶元素赋给ep = S; //用p临时保存栈顶元素空间,以备释放S = S->next; //修改栈顶指针delete p; //释放原栈顶元素的空间return OK;
}bool StackEmpty(LinkStack S) { //判断是否空栈if (!S)return true;return false;
}void CreateBiTree_PreOrder(BiTree &T){ //以先序次序创建二叉树 char ch; cin>>ch;if(ch=='#')T=NULL; else{T=new BiTNode; //生成根结点T->data=ch; //根结点的数据域置为chCreateBiTree_PreOrder(T->lchild);//构造左子树CreateBiTree_PreOrder(T->rchild); //构造右子树}}void InOrder(BiTree T){ //中序遍历的递归递归算法if(T){InOrder(T->lchild);cout<<T->data;InOrder(T->rchild);}
}void InOrder_non_recursion(BiTree T)//中序遍历的非递归算法
{LinkStack S;InitStack (S); BiTree p; BiTree q; p=T;while(p||!StackEmpty(S)){if(p){Push(S,*p); p=p->lchild; //遍历左子树 }else{Pop(S,*q);cout<<q->data; //访问根节点 p=q->rchild; //遍历右子树 }}
}int main() {BiTree T;cout<<"以先序次序创建二叉链表,以#表示空子树:"<<endl;CreateBiTree_PreOrder(T);cout<<"中序序列(递归算法):"; InOrder(T); cout<<"\n中序序列(非递归算法):"; InOrder_non_recursion(T);return 0;
}实验结果:

4、后序遍历的递归与非递归算法的对比:
#include<iostream>
#define OK 1
#define ERROR 0
#define OVERFLOW -2
using namespace std;
typedef char TElemType;
typedef int Status;typedef struct BiTNode{ //二叉树的存储结构TElemType data; // 数据域struct BiTNode *lchild; //左孩子指针struct BiTNode *rchild; //右孩子指针
}BiTNode, *BiTree;typedef struct StackNode { //栈的存储结构BiTNode data; //栈数据元素类型为树结点型 struct StackNode *next;
} StackNode, *LinkStack;Status InitStack(LinkStack &S) { //栈初始化S = NULL;return OK;
}Status Push(LinkStack &S, BiTNode e) { //入栈LinkStack p;p = new StackNode; //生成新结点if (!p) {return OVERFLOW;}p->data = e; //将新结点数据域置为ep->next = S; //将新结点插入栈顶S = p; //修改栈顶指针为preturn OK;
}Status Pop(LinkStack &S, BiTNode &e) { //出栈LinkStack p;if (S == NULL)return ERROR; //栈空e = S->data; //将栈顶元素赋给ep = S; //用p临时保存栈顶元素空间,以备释放S = S->next; //修改栈顶指针delete p; //释放原栈顶元素的空间return OK;
}bool StackEmpty(LinkStack S) { //判断是否空栈if (!S)return true;return false;
}void CreateBiTree_PreOrder(BiTree &T){ //以先序次序创建二叉树 char ch; cin>>ch;if(ch=='#')T=NULL; else{T=new BiTNode; //生成根结点T->data=ch; //根结点的数据域置为chCreateBiTree_PreOrder(T->lchild);//构造左子树CreateBiTree_PreOrder(T->rchild); //构造右子树}}void PostOrder(BiTree T){ //后序遍历的递归递归算法if(T){PostOrder(T->lchild);PostOrder(T->rchild);cout<<T->data;}
}void PostOrder_non_recursion(BiTree T)//后序遍历的非递归算法
{LinkStack l_S,r_S;InitStack (l_S);InitStack (r_S);BiTree p,q; p=T;Push(l_S,*p);while(!StackEmpty(l_S)){Pop(l_S, *q);Push(r_S,*q);if(q->lchild){Push(l_S, *q->lchild);}if(q->rchild){Push(l_S,*q->rchild);}}while(!StackEmpty(r_S)){Pop(r_S,*q);cout<<q->data;}
}int main() {BiTree T;cout<<"以先序次序创建二叉链表,以#表示空子树:"<<endl;CreateBiTree_PreOrder(T);cout<<"后序序列(递归算法):"; PostOrder(T); cout<<"\n后序序列(非递归算法):"; PostOrder_non_recursion(T);return 0;
}实验结果:

4.结语
对于先序、中序和后序遍历,如果采用非递归算法,则需要借助栈来实现。对于二叉树而言,还有一种大家更为熟知的遍历方式,那就是层次遍历。实现对二叉树的层次遍历,则需要借助队列来实现。实现对二叉树的层次遍历,可以参考C实现二叉树的层次遍历
欢迎大家一起来交流~
相关文章:

【数据结构二叉树】C非递归算法实现二叉树的先序、中序、后序遍历
引言: 遍历二叉树:指按某条搜索路径巡访二叉树中每个结点,使得每个结点均被访问一次,而且仅被访问一次。 除了层次遍历外,二叉树有三个重要的遍历方法:先序遍历、中序遍历、后序遍历。 1、递归算法实现先序、中序、后…...

解决网盘资源搜索难题的利器——全面解析哎哟喂啊盘搜及其优秀推荐平台
海量的资源让我们的选择更加丰富,但同时也带来了资源搜索的诸多痛点。无论是寻找最新的影视资源、软件工具,还是各类学习资料,用户常常面临以下几个问题: 资源更新不及时:很多平台资源更新缓慢,用户难以第一时间获取最新内容。 搜索效率低下:关键词搜索不精准,导致需要翻阅大量…...

草料二维码:低成本高效率的访客管理解决方案
在当前的商业和政治环境中,企业和政府机构越来越重视安全保密措施,尤其是对外来人员的行踪记录和管理。访客管理已成为企业运营中不可或缺的一环,它不仅提升了安全性,还增强了效率和便捷性。然而,许多机构仍在使用传统…...

qt管理系统框架(好看界面、漂亮界面、好看的界面、漂亮的界面)
概述 最近一个项目用QT开发,然后找了美工帮设计了下界面。总算完工,后想一下干脆抽出一个基础框架,方便以后用。 功能 支持mysql、echarts。 支持加载动态权限菜单,轻松权限控制。 支持遮罩对话框、抽屉 支持开机启动动画界面 内…...
在VSCode中读取Markdown文件
在VSCode安装Markdown All in One或Markdown Preview Enhanced即可 插件Markdown All in One GitHub:https://github.com/yzhang-gh/vscode-markdown v3.6.2下载链接:https://marketplace.visualstudio.com/_apis/public/gallery/publishers/yzhang/vs…...

Linux rabbitmq客户端 SimpleAmqpClient 源码编译
SimpleAmqpClient的编译成库,加入到工程中 1、下载SimpleAmqpClient 源码: git克隆的路径为:https://github.com/alanxz/SimpleAmqpClient.git 下载压缩包路径:https://codeload.github.com/alanxz/SimpleAmqpClient/zip/maste…...

一台手机可以登录运营多少个TikTok账号?
很多TikTok内容创作者和商家通过运营多个账号来实现品牌曝光和产品销售,这种矩阵运营方式需要一定的技巧和设备成本,那么对于很多新手来说,一台手机可以登录和运营多少个TikTok账号呢? 一、运营TikTok账号的数量限制 TikTok的官…...

Python毕业设计选题:基于Hadoop的租房数据分析系统的设计与实现
开发语言:Python框架:flaskPython版本:python3.7.7数据库:mysql 5.7数据库工具:Navicat11开发软件:PyCharm 系统展示 系统首页 房屋信息详情 个人中心 管理员登录界面 管理员功能界面 用户管理界面 房屋信…...

k8s Service四层负载:服务端口暴露
在 Kubernetes 中,通过 Service 可以实现四层(L4)负载均衡,将流量分发至后端的 Pod。四层负载主要用于传输层(TCP/UDP),而不像七层负载均衡(HTTP/HTTPS)那样进行应用层的…...

QT 关于mousePressEvent无法过滤
QT 关于mousePressEvent无法过滤 bool Filter::eventFilter(QObject *watched, QEvent *event) {// 判断是不是点击事件if((event->type() QEvent::MouseButtonPress) || (event->type() QEvent::MouseButtonDblClick)){//打印一个全局变量static int globalVar 0;gl…...

【VScode】深度对比:Cursor与VScode(CodeMoss)工具,谁才是你的GPT编程最佳助手?
文章目录 一、Cursor的强大功能1.1 Cursor的主要特点1.2 Cursor的使用技巧 二、CodeMoss的功能2.1 CodeMoss的主要特点2.2 CodeMoss的使用技巧 三、Cursor与CodeMoss的对比分析3.1 功能对比3.2 性能对比 四、总结与展望 在科技迅猛发展的今天,AI编程工具如雨后春笋般…...

大数据计算里的-Runtime Filter
文章目录 Runtime Filter示例 Runtime Filter 从纸面意义来看,就是程序在运行时,根据实际的数据去进行一些过滤操作。这和静态的规则优化不同,静态优化不考虑实现的数据的分布。 示例 select a.* ,b.* a join b on a.idb.id假设一下数据…...
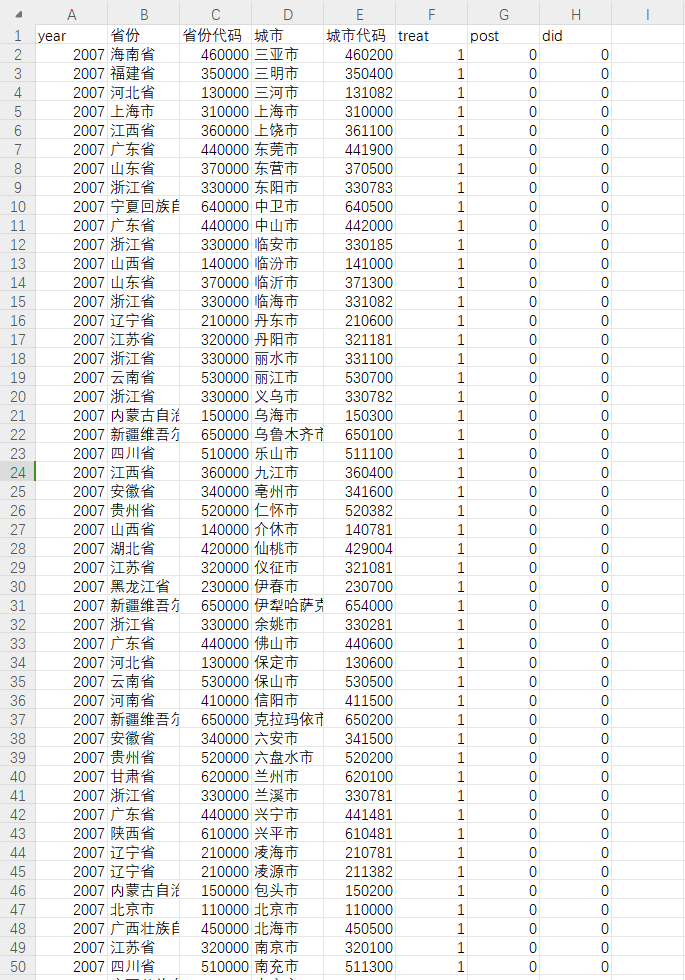
【工具变量】大数据管理机构改革DID(2007-2023年)
数据简介:数字ZF是指以新一代信息技术为支撑,重塑政务信息化管理架构、业务架构、技术架构的现代化治理模式。随着数字政府的建设,特别是借助大数据等新一代数字技术,极大地提升了政府的治理能力,从而起到辅助监管机构…...

Linux -- 初识信号
目录 什么是信号? 如何使用信号? 代码: testSig.cc makefile: 验证: 2号信号: 9号信号: 建立对信号的认识: 信号的处理 自定义信号的处理方式: signal 函数…...

Ubuntu系统如何实现键盘按键映射到其他按键(以 Ctrl+c 映射到 F3,Ctrl+v 映射到 F4 为例)
文章目录 写在前面1. 功能描述2. 实现步骤2.1 安装AutoKey2.2 软件设置2.2.1 软件设置 2.3 测试是否安装成功 参考链接 写在前面 自己的测试环境: Ubuntu20.04 1. 功能描述 Ubuntu系统使用Ctrlc 、Ctrlv 进行复制粘贴操作的时候,时间长了就会出现小拇指…...

el-select、el-autocomplete的选项内容过长显示完整内容
问题: el-select、el-autocomplete的选项内容过长需要看清完整内容 解决方案: 使用el-popover悬停显示完整内容 代码: <el-form-item label"备注" prop"remark"><el-autocomplete v-model"form.remar…...

Go-单元测试
单元测试 测试用例的命名必须是以xxx_test.go的格式 测试用例函数必须以TestXxx开头,一般来说是Test被测试函数名,且必须为大驼峰命名 TestAdd(t *tesing.T)的形参类型必须是*tesing.T 运行测试用例指令 cmd>go test 运行正确,无日志&a…...

【Linux】IPC 进程间通信(一):管道(匿名管道命名管道)
✨ 无人扶我青云志,我自踏雪至山巅 🌏 📃个人主页:island1314 🔥个人专栏:Linux—登神长阶 ⛺️ 欢迎关注:👍点赞 &#…...

Kotlin类与对象
类的定义与对象创建 类的创建是比较简单的,主要是看一下注意点: 1.如果主构造函数没有任何注释或可见性修饰符,则可以省略constructor关键字,如果类中没有其他内容要写,可以直接省略花括号,最后就变成下面…...

Windows版 nginx安装,启动,目录解析,常用命令
Windows版 nginx安装,启动,目录解析,常用命令 一级目录二级目录三级目录 1. 下载2. 启动方式一:方式二: 3. 验证是否启动4. 安装目录解析5. 常用命令 一级目录 二级目录 三级目录 1. 下载 官网下载:ngi…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...
