搜索引擎语法大全(Google、bing、baidu)
搜索引擎语法大全
搜索引擎语法通常指的是在搜索引擎中使用特定的运算符和语法来优化搜索结果。
-
提高搜索精度:使用特定的语法可以帮助用户更精确地找到相关信息,避免无关结果。例如,通过使用引号搜索确切短语,可以确保搜索结果包含该短语的完整性。
-
排除不相关内容:通过运算符(如减号)可以有效排除某些词,使得搜索结果更加聚焦于用户感兴趣的内容。
-
扩展搜索范围:使用逻辑运算符(如 OR)可以同时搜索多个相关主题,帮助用户获取更多信息。
-
限制搜索范围:使用如
site:或filetype:的语法,可以限制搜索到特定网站或文件类型,便于用户快速找到特定资源。 -
优化信息获取:通过组合多种搜索语法,用户可以快速筛选出大量信息中的关键内容,提高信息获取的效率。
-
增强检索能力:对研究人员、学生或专业人士来说,掌握搜索引擎语法可以帮助他们在大量文献或数据中迅速找到所需信息。
总之,搜索引擎语法是提高搜索效率和效果的重要工具。
一、bing和百度语法
bing语法和百度语法基本上是一样的所以整合在一起了,搜索引擎提供了非常丰富的高级搜索语法,使用高级关键字可获取更好的搜索结果,使用关键字可以缩小搜索范围,让你快速找到真正需要的内容。
| 关键字 | 定义 | 示例 | 注意事项 |
|---|---|---|---|
| site | 您可以使用site:搜索不超过两层的Web域、顶级域及目录等子域名。 您还可以在一个网站上搜索包含特定搜索字词的网页。 | 在互联网的世界里”网站上搜索有关SEO的网页,请键入site:www.chinaz.com seo | 注意:“site:”后面跟的站点域名,不要带“http://”。site:和站点名之间,不要带空格。 |
| inurl | 搜索 到的网站结果,将显示包含指定内容的网站。 | 在搜索框中输入 inurl:操作手册 | inurl:和后面的 不要空格 |
| intitle | 网页标题一定要涵盖后面的关键词 | intitle:登录,搜索的网站标题一定有登录 | intitle:和后面的关键词之间不要有空格。 |
| inanchor | 指定搜索条件定位标记的网页。为搜索条件指定一个关键字 | inanchor:msn 查找定位标记中包含 msn的网页 | 关键词之间不要有空格。 |
| inbody | 指定搜索条件正文的网页。为搜索条件指定一个关键字 | inbody:seo 正文中包含 seo 的网页 | 关键词之间不要有空格。 |
| contains | 只搜索包含指定文件类型的链接的网站。 | 音乐 contains:wma 搜索只包含 .wma 文件链接的网站 |
二、Google语法
谷歌有十几种搜索指令,使用这些语法指令可以帮助我们更加准确地查找信息。重要提示:命令中引号、逗号、冒号等标点均需要英文
| 指令 | 用法 | 示例 |
|---|---|---|
| ""(引号) | 用引号来查询一个确切的单词或短语 | 查找有关《百年孤独》这本书的网页,语法:"百年孤独" |
| OR(或者) | 用OR分隔搜索词,同时执行两个搜索查询,这将找到包含多个单词之一的页面。 | 搜索引用了“Google Drive”、“Dropbox”或“OneDrive”的页面,语法:Google Drive OR Dropbox OR OneDrive |
| -(减号、连字符) | 在单词或网站前使用连字符将其从搜索结果中排除 | 从搜索结果中排除维基百科页面,语法:- site:http://wikipedia.org |
| allintext: | 使用allintext:[搜索短语]查找正文中包含这些单词的页面 | 查找正文中有关Roth、IRA投资讯息的页面,语法:allintext:Roth IRA 投资 |
| allintitle: | 使用allintitle:[搜索短语]查找标题中包含这些单词的页面 | 查找标题中同时包含“Apple”和“notebook”的页面,语法:allintitle:Apple notebook |
| allinurl: | 使用allinurl:[搜索短语]查找URL中包含这些单词的页面 | 查找URL中同时包含”Microsoft” and “Surface”的页面,语法:allinurl:Microsoft Surface |
| site: | 使用site:[URL]将搜索结果限制到特定网站 | 查找云点SEO网关于谷歌SEO的页面,语法:site:http://yundianseo.com 谷歌SEO |
| ~(波浪号) | 使用波浪号获得目标关键词及其近似词的搜索结果 | 查找SEO方面的策略或者教程,语法:SEO ~教程 |
| related: | 使用related:[URL]查找与特定网站类似的网站 | 查找与云点SEO类似的网站,语法:related:http://yundianseo.com |
| define: | 使用define:[搜索短语]查找其定义 | 查找SEO的定义,语法:define:SEO |
| $ | 使用$查找特定价格的商品 | 查找一款售价在99美金的手机,语法:mobile phone $99 |
| location: | 使用location:[地点]查看某个地区内的相关信息 | 查询南京的酒店,语法:hotel location:Nanjing |
| *(星号) | 添加星号作为未知单词或事实的占位符 | 查找以“生活就像一个”开头的引语,语法:生活就像一个* |
| filetype: | 使用filetype:[后缀]将结果限制为特定的文件格式,如PDF或DOC。 | 查找PDF格式的Microsoft Office键盘快捷键相关文件,语法:filetype:pdf Microsoft Office键盘快捷键 |
| ..(两点) | 用两个句点分隔数字,不带空格,以搜索该范围内的数字 | 查找1950年至2000年间发生的计算机里程碑,语法:”计算机里程碑” 1950..2000 |
| AROUND(n) | 在两个搜索词之间加上AROUND(n),以查找两个词间有特定距离的页面。用数字n设置术语之间的最大距离,这对于查找两个搜索词之间的关系很有用。 | 查找在同一句话或段落中提到Facebook和Microsoft的页面,语法:Facebook AROUND(7) Microsoft |
结语:
搜索引擎语法的通配符很多都是相通的,如OR、""、-、*、+之类的符号,不同的语句搭配使用,不同语句之前中间要加空格。
-
引号 (" "):用于搜索确切短语。例如,搜索
"人工智能"将返回包含这个确切短语的结果。 -
减号 (-):用于排除某个词。例如,搜索
苹果 -水果将返回与“苹果”相关但不包含“水果”的结果。 -
星号 (*):作为通配符,用于替代一个或多个词。例如,搜索
机器学习 * 应用可以找到“机器学习”的不同应用场景。 -
加号 (+) :查询词用加号+语法可以帮您在搜索结果中必需包含特定的关键词所有网页。例子:电影 +qvod查询词“电影”在搜索结果中,“qvod”被必需被包含在搜索结果中。
相关文章:
)
搜索引擎语法大全(Google、bing、baidu)
搜索引擎语法大全 搜索引擎语法通常指的是在搜索引擎中使用特定的运算符和语法来优化搜索结果。 提高搜索精度:使用特定的语法可以帮助用户更精确地找到相关信息,避免无关结果。例如,通过使用引号搜索确切短语,可以确保搜索结果包…...

java设计模式之行为型模式(11种)
行为型模式 行为型模式用于描述程序在运行时复杂的流程控制,即描述多个类或对象之间怎样相互协作共同完成单个对象都无法单独完成的任务,它涉及算法与对象间职责的分配。 行为型模式分为类行为模式和对象型模式,前者采用继承机制来在类间分派…...

微服务系列一:基础拆分实践
目录 前言 一、认识微服务 1.1 单体架构 VS 微服务架构 1.2 微服务的集大成者:SpringCloud 1.3 微服务拆分原则 1.4 微服务拆分方式 二、微服务拆分入门步骤 :以拆分商品模块为例 三、服务注册订阅与远程调用:以拆分购物车为例 3.1 …...

leetcode 1470.重新排列数组
1.题目要求: 2.题目代码: class Solution { public:vector<int> shuffle(vector<int>& nums, int n) {vector<int> x_array(nums.begin(),nums.begin() n);vector<int> y_array(nums.begin() n,nums.end());int x_index 0;int y_index 0;for…...

windows在两台机器上测试 MySQL 集群实现实时备份
在两台机器上测试 MySQL 集群实现实时备份的基本步骤: 一、环境准备 机器配置 确保两台机器(假设为服务器 A 和服务器 B)能够互相通信,例如它们在同一个局域网内,并且开放了 MySQL 通信所需的端口(默认是 …...

点晴模切ERP系统助力模切企业转型升级之路
随着我国制造业规模不断扩大,中国制造业已经从高速扩张转向深入挖潜的关键阶段。数字化转型不仅有助于提升企业的生产效率和管理水平,还能有效应对市场竞争,实现可持续发展。在数字化转型的过程中,企业资源规划(ERP&am…...

redis修改配置文件配置密码开启远程访问后台运行
编辑 Redis 配置文件 编辑 /etc/redis/redis.conf,设置必要的参数。 sudo vim /etc/redis/redis.conf设置后台运行: 找到以下行,将 no 改为 yes: daemonize yes设置密码: 找到以下行,取消注释并设置密码为…...
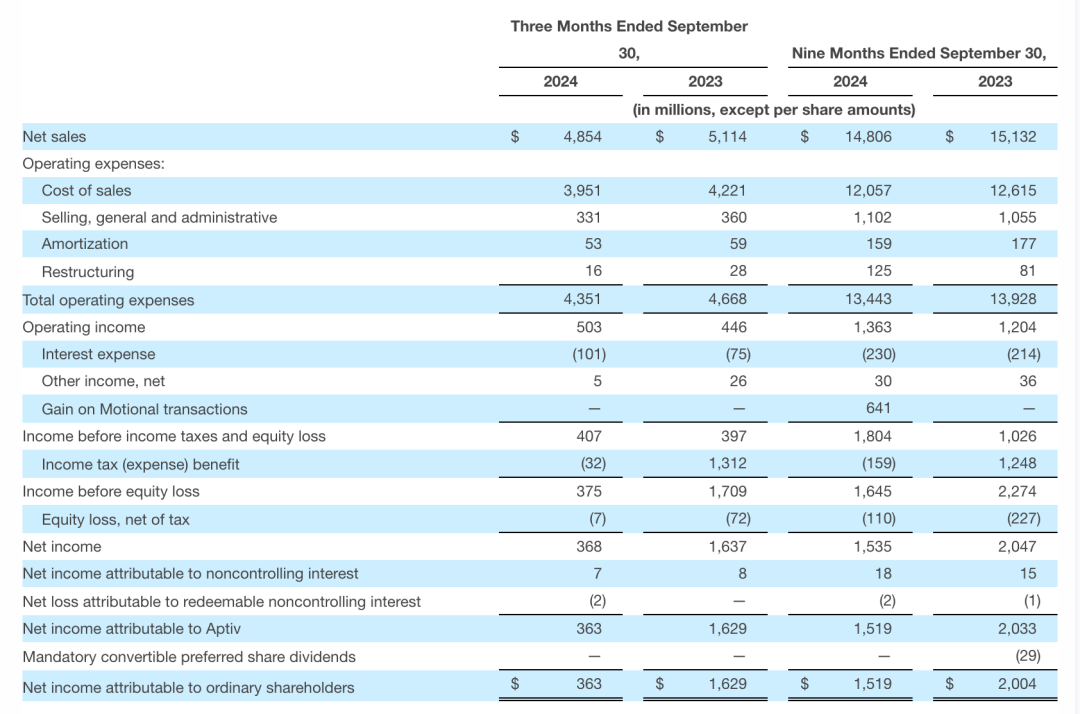
市场分化!汽车零部件「变天」
全球汽车市场的动荡不安,还在持续。 本周,全球TOP20汽车零部件公司—安波福(Aptiv)发布2024年第三季度财报显示,三季度公司经调整后确认收入同比下降6%;按照区域市场来看,也几乎是清一色的下滑景…...

SCSS在Vue中的用法
SCSS在Vue中的用法 一、安装相关依赖1、安装sass - loader和node - sass(或dart - sass) 二、在组件中使用SCSS1、单文件组件(.vue)中的样式使用2、**全局样式使用SCSS**3、在组件中使用变量和混入(Mixins)…...

CPU用户时间百分比
在计算机系统中,"CPU用户时间百分比(CPU User Time)"是一个性能监控指标,它描述了CPU在用户模式下执行的累积时间与总的CPU时间的比例。这个指标可以帮助我们了解系统在执行用户态程序时的负载情况。下面是一些关于CPU用…...

RN中的StyleSheet
一、RN中样式的特点 RN的样式和前端的CSS的样式有一些区别。主要如下: RN中的样式 前端的CSS 继承性 没有继承性 有继承性 命名 fontSize(小驼峰命名) font-size 尺寸单位 with: 100 With: 100px 特殊的样式名 marginHorizontal…...

Swift 开发教程系列 - 第1章:Swift 简介与开发环境配置
在开始开发 Swift 应用之前,了解 Swift 语言的背景和设置开发环境非常重要。接下来,我们将逐步介绍 Swift 的基本概念,并带你完成开发环境的安装和项目创建。 1.1 Swift 简介 Swift 是由 Apple 开发的一种现代化编程语言,于 201…...
)
躺平成长-下一个更新的数据(躺平成长数据显示核心)
旭日图(Sunburst Chart)是一种用于展示具有层次结构数据的可视化图表。 开源竞争: (当你无法掌握技术的时候,就开源这个技术,培养出更多的技术依赖,让更多的人帮助你完善你的技术,那…...

你们接口怎么测?有没有完完整整的把一个接口测下来?
面试官在问到这道问题的时候,我们应该这么去回答,根据自己技术掌握的水准进行由浅入深的回答。 基础: 我们接口测试之前,开发都会有一份接口文档给到我们,我们要分析接口中的入参和响应。 针对入参的参数类型和参数…...

Pinia-状态管理
Pinia-状态管理 特点: 1. 轻量和模块化 Pinia 是一个轻量级的状态管理库,支持模块化管理,即可以将应用的状态分成多个 store 以实现更好的组织。使用 Pinia,可以定义多个 store,每个 store 都是一个独立的模块&#x…...

IP系列之bscan讨论
1、做Bcan前首先要确定ip_vender是否已经在phy_level做好了bscan_chian??? 若已经做好,那么vender会给一个XXX.bsdl文件,结合详细的ip文档指导手册,确定bscan_chain是在内部的tap下挂着,还是单…...

Centos安装配置Jenkins
下载安装 注意:推荐的LTS版本对部分插件不适配,直接用最新的版本,jenkins还需要用到git和maven,服务器上已经安装,可查看参考文档[1]、[2],本次不再演示 访问开始使用 Jenkins 下载jenkins 上传至服务器…...
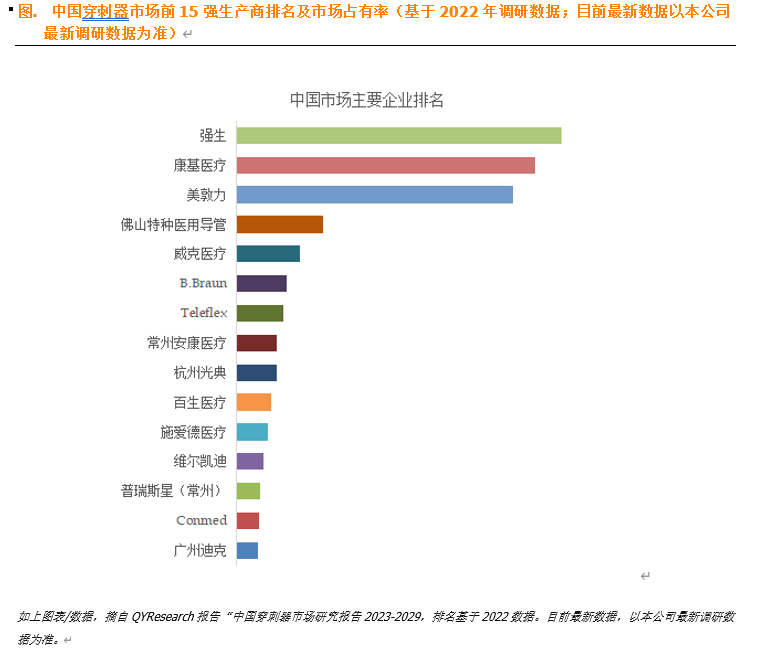
创新医疗突破:新型穿刺器显著提高手术安全性与效率
据QYResearch调研团队最新报告“中国穿刺器市场报告2023-2029”显示,预计2029年中国穿刺器市场规模将达到18.5亿美元,未来几年年复合增长率CAGR为18.1%。 如上图表/数据,摘自QYResearch最新报告“中国穿刺器市场研究报告2023-2029. 如上图表/…...

【MySQL】可重复读级别下基于Next Key Lock解决幻读
昨天读到了一篇文章[1],里面讲,面试官说mysql的可重复读级别下有解决幻读的方式,最后公布了答案,是在sql后面加for update。这么说倒是没错,但是这种问法给我一种奇怪的感觉,因为for update无论在哪个隔离级…...

【安全性分析】正式安全分析与非正式安全分析
安全性分析-系列文章目录 第一章 【安全性分析】正式安全分析与非正式安全分析 第二章 【安全性分析】BAN逻辑 (BAN Logic) 文章目录 安全性分析-系列文章目录前言一、正式安全分析1. 理想化模型(如随机预言机模型)2. 标准模型(Standard Model)3. 形式化验证4. 数学证明二…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...
