算法妙妙屋-------1.递归的深邃回响:二叉树的奇妙剪枝
大佬们好呀,这一次讲解的是二叉树的深度搜索,大佬们请阅
1.前言
⼆叉树中的深搜(介绍)
深度优先遍历(DFS,全称为DepthFirstTraversal),是我们树或者图这样的数据结构中常⽤的⼀种***遍历算法***。这个算法会尽可能深的搜索树或者图的分⽀,直到⼀条路径上的所有节点都被遍历完毕,然后再回溯到上⼀层,继续找⼀条路遍历。
在⼆叉树中,常⻅的深度优先遍历为:前序遍历、中序遍历以及后序遍历。
因为树的定义本⾝就是递归定义,因此采⽤递归的⽅法去实现树的三种遍历不仅容易理解⽽且代码很简洁。并且前中后序三种遍历的唯⼀区别就是 ***访问根节点的时机不同***,在做题的时候,选择⼀个适当的遍历顺序,对于算法的理解是⾮常有帮助的。
好了,接下来让我们用习题来介绍吧
1.计算布尔⼆叉树的值(medium)
题目链接:计算布尔二叉树的值
题目介绍:
给你⼀棵完整⼆叉树的根,这棵树有以下特征:
叶⼦节点要么值为0要么值为1,其中0表⽰False,1表⽰True。
⾮叶⼦节点要么值为2要么值为3,其中2表⽰逻辑或OR,3表⽰逻辑与AND。
计算⼀个节点的值⽅式如下:
如果节点是个叶⼦节点,那么节点的值为它本⾝,即True或者False。
否则,计算两个孩⼦的节点值,然后将该节点的运算符对两个孩⼦值进⾏运算。
返回根节点root的布尔运算值。
完整⼆叉树是每个节点有0个或者2个孩⼦的⼆叉树。
叶⼦节点是没有孩⼦的节点。

算法思路:
-
- 对于规模为n的问题,需要求得当前节点值。
-
- 节点值不为0或1时, ***
规模为n的问题可以被拆分为规模为n-1的⼦问题***:
- 节点值不为0或1时, ***
- a:所有⼦节点的值;
- b:通过⼦节点的值运算出当前节点值。
-
- 当问题的规模变为n=1时,即叶⼦节点的值为0或1,我们可以
直接获取当前节点值为0或1。
- 当问题的规模变为n=1时,即叶⼦节点的值为0或1,我们可以
递归函数流程:
-
- 当前问题规模为n=1时,即叶⼦节点,直接返回当前节点值
-
- 递归求得左右⼦节点的值;
-
- 通过***判断当前节点的逻辑运算符***,计算左右⼦节点值运算得出的结果;
代码如下:
class Solution {
public:bool evaluateTree(TreeNode* root) {if(root->left==nullptr||root->right==nullptr){return root->val;}else{if(root->val==2)return evaluateTree(root->left)||evaluateTree(root->right);elsereturn evaluateTree(root->left)&&evaluateTree(root->right);}}
};
2. 求根节点到叶节点数字之和(medium)
题目链接:求根节点到叶节点数字之和
题目介绍:
给你⼀个⼆叉树的根节点root,树中每个节点都存放有⼀个0到9之间的数字。
每条从根节点到叶节点的路径都代表⼀个数字:
例如,从根节点到叶节点的路径1->2->3表⽰数字123。
计算从根节点到叶节点⽣成的所有数字之和。
叶节点是指没有⼦节点的节点。

解题思路:
解法(dfs-前序遍历):
前序遍历按照根节点、左⼦树、右⼦树的顺序遍历⼆叉树的所有节点,通常⽤于 ⼦节点的状态依赖于⽗节点状态的题⽬。
在前序遍历的过程中,我们可以 往左右⼦树传递信息,并且在回溯时得到左右⼦树的返回值。递归函数可以帮我们完成两件事:
- 将⽗节点的数字与当前节点的信息整合到⼀起,计算出当前节点的数字,然后传递到下⼀层进⾏递归;
- 当遇到叶⼦节点的时候,就***不再向下传递信息***,⽽是 ***
将整合的结果向上⼀直回溯到根节点***。在递归结束时,根节点需要返回的值也就被更新为了整棵树的数字和。
递归函数流程:
-
- 当遇到空节点的时候,说明这条路从根节点开始没有分⽀,返回0;
-
- 结合⽗节点传下的信息以及当前节点的val,
计算出当前节点数字sum;
- 结合⽗节点传下的信息以及当前节点的val,
-
- 如果当前结点是叶⼦节点,
直接返回整合后的结果sum
- 如果当前结点是叶⼦节点,
-
- 如果当前结点不是叶⼦节点,将sum传到左右⼦树中去,得到左右⼦树中节点路径的数字和,然后 ***
相加后返回结果***。
- 如果当前结点不是叶⼦节点,将sum传到左右⼦树中去,得到左右⼦树中节点路径的数字和,然后 ***
代码如下:
class Solution {
public:int sumNumbers(TreeNode* root) {return sumNumber(root,0);}int sumNumber(TreeNode* root,int x) {if(root==nullptr)return x;else{x=x*10+root->val;}if(root->left!=nullptr&&root->right!=nullptr)return sumNumber(root->left,x)+sumNumber(root->right,x);else if(root->left!=nullptr)return sumNumber(root->left,x);else if(root->right!=nullptr)return sumNumber(root->right,x);elsereturn x;}
};
3.⼆叉树剪枝(medium)
题⽬链接:二叉树剪枝
题目介绍:
给你⼆叉树的根结点root,此外树的每个结点的值要么是0,要么是1。
返回移除了所有不包含1的⼦树的原⼆叉树。
节点node的⼦树为node本⾝加上所有node的后代。

解法(dfs-后序遍历):
后序遍历按照左⼦树、右⼦树、根节点的顺序遍历⼆叉树的所有节点,通常⽤于 ⽗节点的状态依赖于⼦节点状态的题⽬。
后序遍历的主要流程:
-
- 递归出⼝:当传⼊节点为空时,不做任何处理;
-
- 递归处理***左⼦树***;
-
- 递归处理***右⼦树***;
-
- 处理当前节点:判断该节点是否为叶⼦节点(即左右⼦节点均被删除,前点成为叶⼦节点),
并且节点的值为0:
a. 如果是,就删除掉;
b. 如果不是,就不做任何处理。
- 处理当前节点:判断该节点是否为叶⼦节点(即左右⼦节点均被删除,前点成为叶⼦节点),
代码如下:
class Solution {
public:TreeNode* pruneTree(TreeNode* root) {dfs(root);if(root->left==nullptr&&root->right==nullptr&&root->val==0)return nullptr;elsereturn root;}bool dfs(TreeNode* root) {if (root) {if(root->left==nullptr&&root->right==nullptr)return root->val;bool l = dfs(root->left);bool r = dfs(root->right);if (l == false) {root->left = nullptr;}if (r == false) {root->right = nullptr;}if(root->val==0)return l || r;elsereturn 1;}elsereturn false;}
};
4. ⼆叉搜索树中第k⼩的元素(medium)
题目链接:⼆叉搜索树中第k⼩的元素
题目描述:
给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 小的元素(从 1 开始计数)。

解题思路:
(中序遍历+计数器剪枝)
上述解法不仅使⽤⼤量额外空间存储数据,并且会将所有的结点都遍历⼀遍。
但是,我们可以根据中序遍历的过程,只需扫描前k个结点即可。
因此,我们可以创建⼀个全局的计数器***count***,将其初始化为***k***,每遍历⼀个节点就将***count–***。直到某次递归的时候,count的值等于0,说明此时的结点就是我们要找的结果。
代码如下:
class Solution {
public:int kthSmallest(TreeNode* root, int k) {int flag = 0;dfs(root, k, flag);return flag;}void dfs(TreeNode* root, int& k, int& flag) {if (root) {dfs(root->left, k, flag);k--;if (k == 0) {flag = root->val;}dfs(root->right, k, flag);}}
};
好啦,递归问题就讲到这里,下一次讲解的是搜索,回溯和全排列,我们下次再见
相关文章:

算法妙妙屋-------1.递归的深邃回响:二叉树的奇妙剪枝
大佬们好呀,这一次讲解的是二叉树的深度搜索,大佬们请阅 1.前言 ⼆叉树中的深搜(介绍) 深度优先遍历(DFS,全称为DepthFirstTraversal),是我们树或者图这样的数据结构中常⽤的⼀种…...

编写第一个 Appium 测试脚本:从安装到运行!
前言 最近接到一个测试项目,简单描述一下,需求就是:一端发送指令,另一端接受指令并处理指令。大概看了看有上百条指令,点点点岂不是废了,而且后期迭代,每次都需要点点点,想想就头大…...

mysql查表相关练习
作业要求: 单表练习: 1 . 查询出部门编号为 D2019060011 的所有员工 2 . 所有财务总监的姓名、编号和部门编号。 3 . 找出奖金高于工资的员工。 4 . 找出奖金高于工资 40% 的员工。 5 找出部门编号为 D2019090011 中所有财务总监,和…...

airtest+poco多脚本、多设备批处理运行测试用例自动生成测试报告
一:主要内容 框架功能、框架架构及测试报告效果 airtest安装、环境搭建 框架搭建、框架运行说明 框架源码 二:框架功能及测试报告效果 1. 框架功能: 该框架笔者用来作为公司的项目的前端自动化,支持pc和app,本文…...

Prometheus套装部署到K8S+Dashboard部署详解
1、添加helm源并更新 helm repo add prometheus-community https://prometheus-community.github.io/helm-charts helm repo update2、创建namespace kubectl create namespace monitoring 3、安装Prometheus监控套装 helm install prometheus prometheus-community/prome…...

python使用pymysql
为了封装这个数据库操作为一个通用方法,我们可以创建一个函数,该函数接受数据库连接参数(如主机名、用户名、密码、数据库名)、SQL语句以及必要的参数(用于参数化查询)。下面是一个简单的封装示例ÿ…...

Vue3 + TypeScript 组件和文件命名规范及 setup 导入顺序规范
前言 在 Vue3 项目中,合理的文件命名规范和导入顺序不仅有助于提高代码的可读性,还能增强团队协作的效率。特别是在使用 TypeScript 和 Composition API 的项目中,清晰的组件和文件结构尤为重要。本文将详细介绍 Vue3 TypeScript 项目中的组…...

netty之处理连接源码分析
写在前面 在这篇文章看了netty服务是如何启动的,服务启动成功后,也就相当于是迎宾工作都已经准备好了,那么当客人来了怎么招待客人呢?也就是本文要看的处理连接的工作。 1:正文 先启动源码example模块的echoserver&a…...

Dockerfile文件编写
1、打nginx原始包 登录后复制 ROM nginxENV LANG zh_CN.UTF-8 ENV LC_ALL zh_CN.UTF-8 ENV TZ Asia/Singapore# 设置时区,同样保持在一层 RUN ln -sf /usr/share/zoneinfo/${TZ} /etc/localtime && \echo "${TZ}" > /etc/timezoneRUN apt-get …...

Oracle SQL 使用 ROWNUM 分页查询速度太慢的问题及解决方案!
在使用 Oracle 数据库进行数据查询时,分页查询是一种常见的需求。传统上,开发者常常使用 ROWNUM 来实现分页功能。 然而,当数据量较大时,使用 ROWNUM 进行分页查询可能会导致性能问题。本文将深入探讨这一问题的原因,并提供多种解决方案,以提高分页查询的性能。 一、RO…...

Django3 + Vue.js 前后端分离书籍添加项目Web开发实战
文章目录 Django3后端项目创建切换数据库创建Django实战项目App新建Vue.js前端项目 Django3后端项目创建 创建Django项目,采用Pycharm或者命令行创建皆可。此处,以命令行方式作为演示,项目名为django_vue。 django-admin startproject djang…...

楼梯区域分割系统:Web效果惊艳
楼梯区域分割系统源码&数据集分享 [yolov8-seg-FocalModulation&yolov8-seg-GFPN等50全套改进创新点发刊_一键训练教程_Web前端展示] 1.研究背景与意义 项目参考ILSVRC ImageNet Large Scale Visual Recognition Challenge 项目来源AAAI Global Al l…...

Day10加一
给定一个由 整数 组成的 非空 数组所表示的非负整数,在该数的基础上加一。 最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。 你可以假设除了整数 0 之外,这个整数不会以零开头。 class Solution {public int[] plusOne(int[] di…...

UTF-8简介
UTF-8 UTF-8(8-bit Unicode Transformation Format)是一种针对Unicode的可变长度字符编码,也是一种前缀码。它可以用一至四个字节对Unicode字符集中的所有有效编码点进行编码,属于Unicode标准的一部分,最初由肯汤普逊…...

基于Openwrt系统架构,实现应用与驱动的实例。
一、在openwrt系统架构,编写helloworld的应用程序。 第一步先创建目录,项目代码要放在 openwrt根目下的 package 目录中,这里源码写在了 hellworld 的 src 目录下,因为外层还有需要编写的文件。 mkdir -p ~/openwrt/package/hel…...

SQL进阶技巧:如何利用三次指数平滑模型预测商品零售额?
目录 0 问题背景 1 数据准备 2 问题解决 2.1 模型构建 (1)符号规定 (2)基本假设...

HTB:Cicada[WriteUP]
目录 连接至HTB服务器并启动靶机 使用nmap对靶机进行开放端口扫描 使用nmap对靶机开放端口进行脚本、服务信息扫描 首先尝试空密码连接靶机SMB服务 由于不知道账户名,这里我们使用crackmapexec对smb服务进行用户爆破 通过该账户连接至靶机SMB服务器提取敏感信…...

小张求职记四
学校食堂的装修富丽堂皇,像个金碧辉煌的宫殿,可实际上却充斥着廉价的塑料制品和刺鼻的消毒水味。这金玉其外败絮其中的景象,与食堂承包商的“精明算计”如出一辙。 小张和小丽应约来到了一个档口下,“红烧肉”,之前就是…...

适用于 c++ 的 wxWidgets框架源码编译SDK-windows篇
本文章记录了下载wxWidgets源码在windows 11上使用visual Studio 2022编译的全过程,讲的不详细请给我留言,让我知道错误并改进。 本教程是入门级。有更深入的交流可以留言给我。 如今互联网流行现在大家都忘记了这块桌面的开发,我认为桌面应用还是有用武之地,是WEB无法替代…...

flink 内存配置(二):设置TaskManager内存
TaskManager在Flink中运行用户代码。根据需要配置内存使用,可以极大地减少Flink的资源占用,提高作业的稳定性。 注意下面的讲解适用于TaskManager 1.10之后的版本。与JobManager进程的内存模型相比,TaskManager内存组件具有类似但更复杂的结构…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...
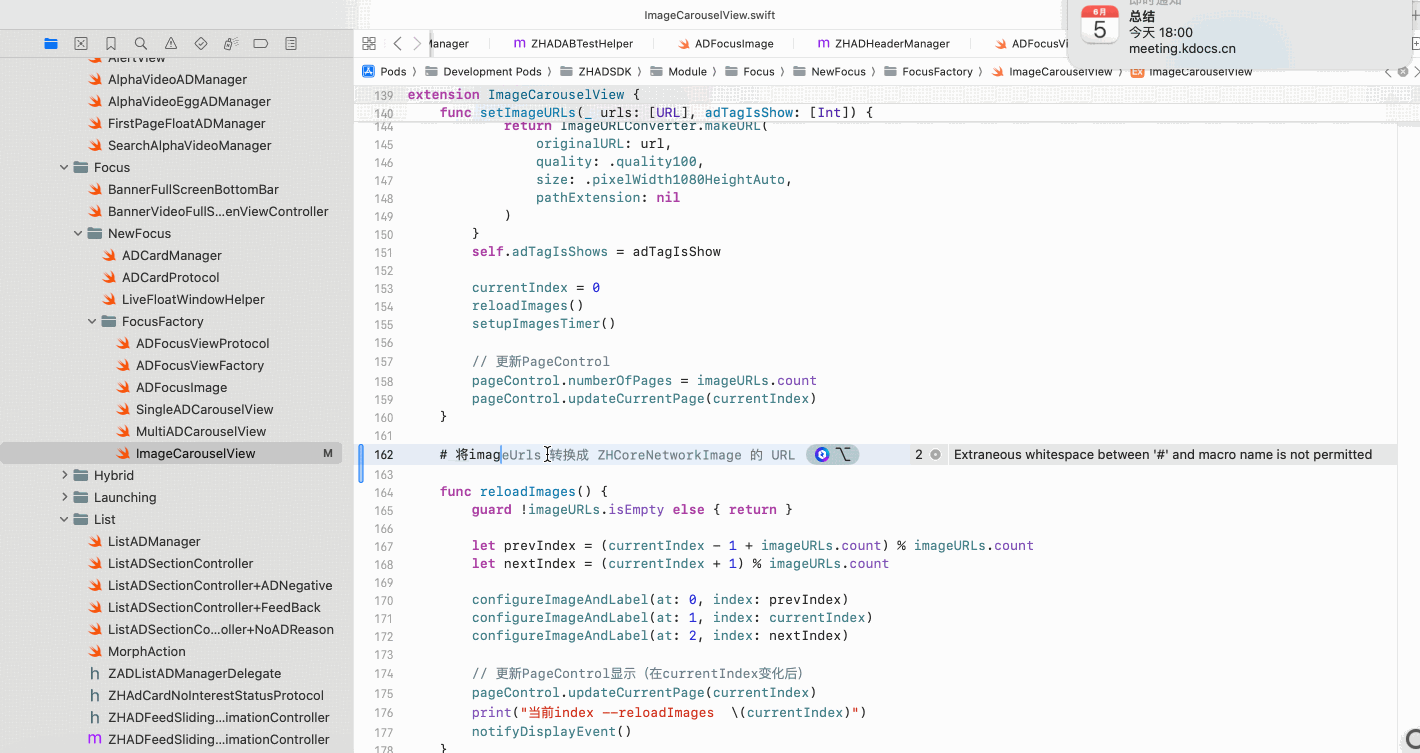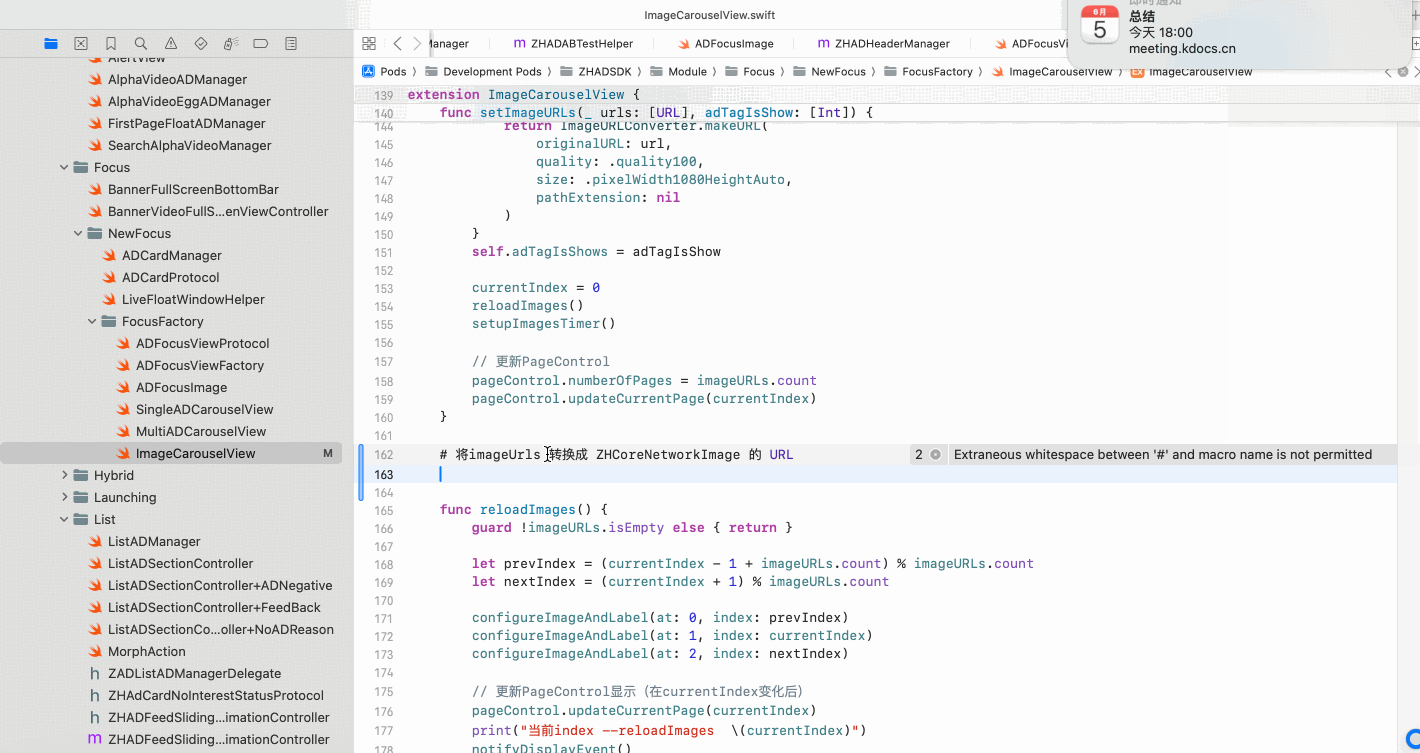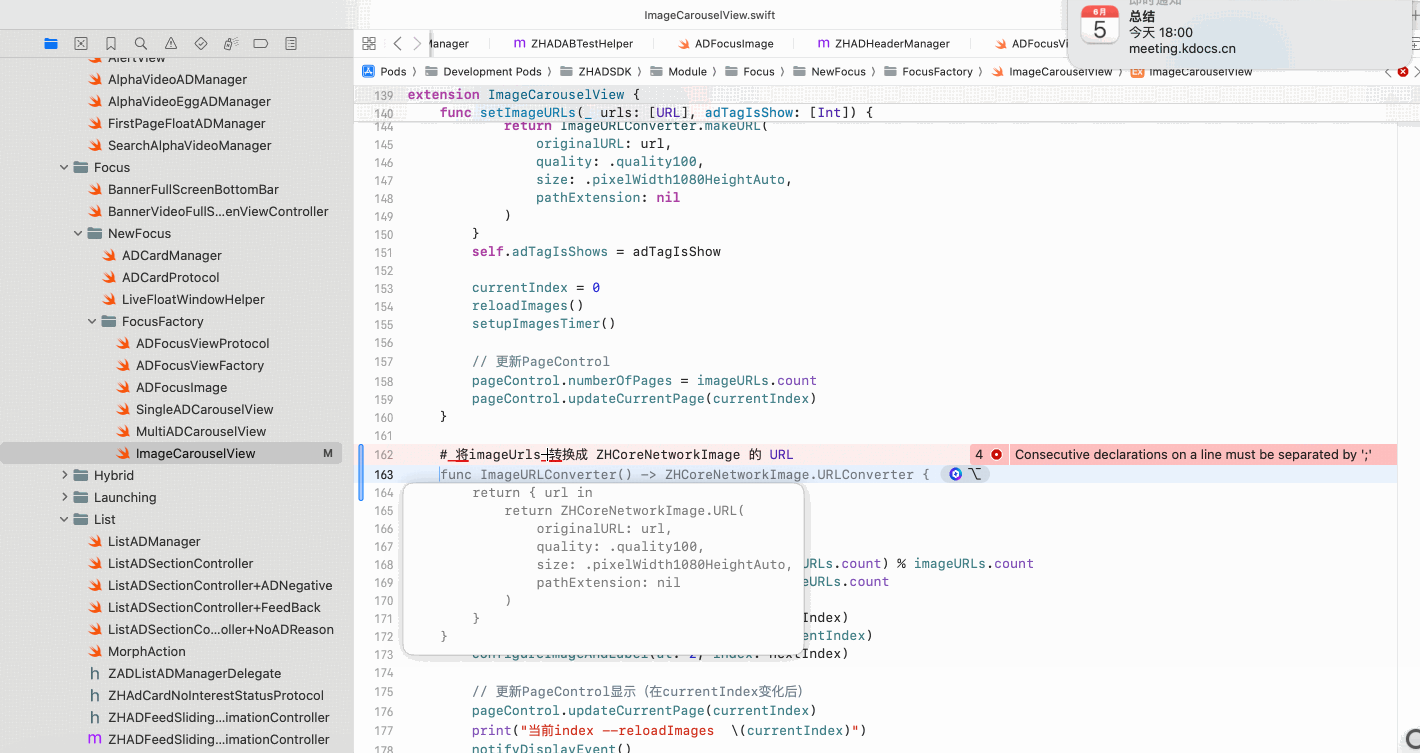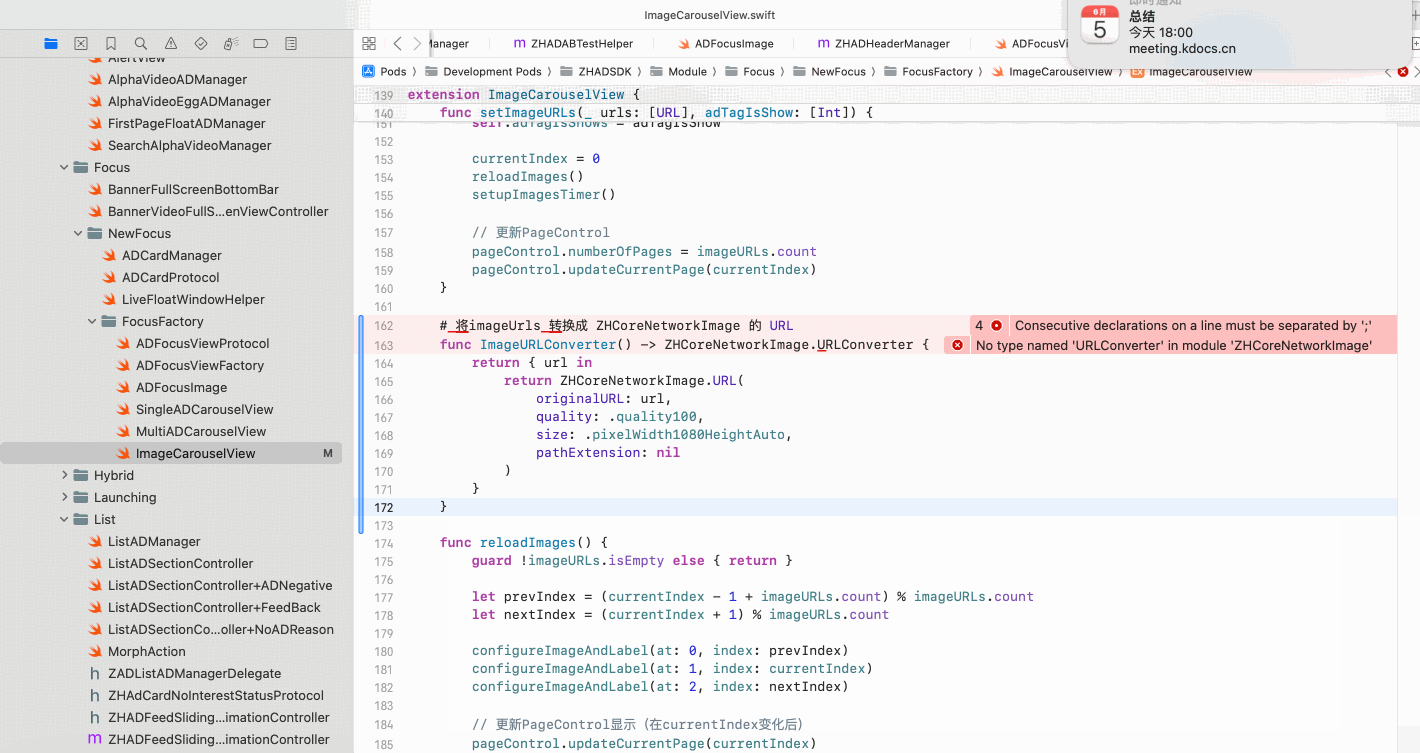
Copilot for Xcode (iOS的 AI辅助编程)
Copilot for Xcode 简介Copilot下载与安装 体验环境要求下载最新的安装包安装登录系统权限设置 AI辅助编程生成注释代码补全简单需求代码生成辅助编程行间代码生成注释联想 代码生成 总结 简介 尝试使用了Copilot,它能根据上下文补全代码,快速生成常用…...

初探用uniapp写微信小程序遇到的问题及解决(vue3+ts)
零、关于开发思路 (一)拿到工作任务,先理清楚需求 1.逻辑部分 不放过原型里说的每一句话,有疑惑的部分该问产品/测试/之前的开发就问 2.页面部分(含国际化) 整体看过需要开发页面的原型后,分类一下哪些组件/样式可以复用,直接提取出来使用 (时间充分的前提下,不…...

SpringCloud优势
目录 完善的微服务支持 高可用性和容错性 灵活的配置管理 强大的服务网关 分布式追踪能力 丰富的社区生态 易于与其他技术栈集成 完善的微服务支持 Spring Cloud 提供了一整套工具和组件来支持微服务架构的开发,包括服务注册与发现、负载均衡、断路器、配置管理等功能…...

今日行情明日机会——20250609
上证指数放量上涨,接近3400点,个股涨多跌少。 深证放量上涨,但有个小上影线,相对上证走势更弱。 2025年6月9日涨停股主要行业方向分析(基于最新图片数据) 1. 医药(11家涨停) 代表标…...
