A*算法求第k短路
话不多说先上例题。。
acwing:178. 第K短路
给定一张 NN 个点(编号 1,2…N1,2…N),MM 条边的有向图,求从起点 SS 到终点 TT 的第 KK 短路的长度,路径允许重复经过点或边。
注意: 每条最短路中至少要包含一条边。
输入格式
第一行包含两个整数 NN 和 MM。
接下来 MM 行,每行包含三个整数 A,BA,B 和 LL,表示点 AA 与点 BB 之间存在有向边,且边长为 LL。
最后一行包含三个整数 S,TS,T 和 KK,分别表示起点 SS,终点 TT 和第 KK 短路。
输出格式
输出占一行,包含一个整数,表示第 KK 短路的长度,如果第 KK 短路不存在,则输出 −1−1。
数据范围
1≤S,T≤N≤10001≤S,T≤N≤1000,
0≤M≤1040≤M≤104,
1≤K≤10001≤K≤1000,
1≤L≤1001≤L≤100输入样例:
2 2 1 2 5 2 1 4 1 2 2输出样例:
14
思路:
整体思路就是先逆向求一次dijkstral,将各点到目标点的最短路求出来,以此作为A*的估计值。然后在采用A*求第K短路,当第K次目标点出队列是,返回值即可。注意起点终点一直时需要将k+1,将原地不动的情况除去。
上代码:
#include<bits/stdc++.h> using namespace std; typedef pair<int,int> PII; typedef pair<int,PII> PIII; #define y second #define x first const int N=1010,M=3e4+10; int s, t ,k; int n,m; int h[N],h2[N],e[M],ne[M],w[M],idx; int dis[N],cnt[N]; bool st[N]; void add(int h[],int a,int b,int c){e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++; } void dijkstral(){memset(dis,0x3f,sizeof(dis));priority_queue<PII,vector<PII>,greater<PII>>q;dis[t]=0;q.push({0,t});while(q.size()){auto T=q.top();q.pop();int u=T.y;if(st[u]){continue;}st[u]=true;for(int i=h2[u];~i;i=ne[i]){int j=e[i];if(st[j]){continue;}if(dis[j]>dis[u]+w[i]){dis[j]=dis[u]+w[i];q.push({dis[j],j});}}} } int astar(){priority_queue<PIII,vector<PIII>,greater<PIII>> q;q.push({dis[s],{0,s}});while(q.size()){auto T=q.top();q.pop();int dist=T.y.x;int u=T.y.y;cnt[u]++;if(cnt[t]==k){return dist;}for(int i=h[u];~i;i=ne[i]){int j=e[i];if(cnt[j]>k){continue;}q.push({dist+w[i]+dis[j],{dist+w[i],j}});}}return -1; } int main() {ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);memset(h,-1,sizeof(h));memset(h2,-1,sizeof(h2));cin>>n>>m;for(int i=1;i<=m;i++){int a,b,c;cin>>a>>b>>c;add(h,a,b,c);add(h2,b,a,c);}cin>>s>>t>>k;dijkstral();if(s==t){k++;}int ans=astar();cout<<ans; }
这里附上一道例题,求次短路。。
算是A*的特殊情况了,去直接秒杀吧。
acwing:133. 第二短路
贝茜把家搬到了一个小农场,但她常常回到 FJ 的农场去拜访她的朋友。
贝茜很喜欢路边的风景,不想那么快地结束她的旅途,于是她每次回农场,都会选择第二短的路径,而不像我们所习惯的那样,选择最短路。
贝茜所在的乡村有 RR 条双向道路,每条路都连接了所有的 NN 个农场中的某两个。
贝茜居住在农场 11,她的朋友们居住在农场 NN(即贝茜每次旅行的目的地)。
贝茜选择的第二短的路径中,可以包含任何一条在最短路中出现的道路,并且一条路可以重复走多次。
当然第二短路的长度必须严格大于最短路(可能有多条)的长度,但它的长度必须不大于所有除最短路外的路径的长度。
输入格式
第一行包含两个整数 NN 和 RR。
接下来 RR 行,每行包含三个整数 A,B,DA,B,D,表示农场 AA 和农场 BB 之间存在一条长度为 DD 的路。
输出格式
输出仅包含一个整数,表示从农场 11 到农场 NN 的第二短路的长度。
数据范围
1≤R≤1051≤R≤105,
1≤N≤50001≤N≤5000,
1≤D≤50001≤D≤5000,
1≤A,B≤N1≤A,B≤N输入样例:
4 4 1 2 100 2 4 200 2 3 250 3 4 100输出样例:
450
#include<bits/stdc++.h> using namespace std; const int N=5010,M=4e5+10; #define x first #define y second typedef pair<int,int>PII; typedef pair<int,PII>PIII; int h[N],e[M],ne[M],w[M],idx; int dis[N]; bool st[N]; int cnt[N]; int n,m;void add(int a,int b,int c){e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++; } void dijkstral() {memset(dis,0x3f,sizeof(dis));priority_queue<PII,vector<PII>,greater<PII>>q;q.push({0,n});dis[n]=0;while(q.size()){auto t=q.top();q.pop();int v=t.y;if(st[v]){continue;}st[v]=true;for(int i=h[v];~i;i=ne[i]){int j=e[i];if(st[j]){continue;}if(dis[j]>dis[v]+w[i]){dis[j]=dis[v]+w[i];q.push({dis[j],j});}}} } int astar(){int flag=0;priority_queue<PIII,vector<PIII>,greater<PIII>>q;q.push({dis[1],{0,1}});while(q.size()){auto t=q.top();q.pop();int v=t.y.y;int dist=t.y.x;cnt[v]++;if(cnt[n]==1){flag=dist;}if(cnt[n]>=2&&dist>flag){return dist;}for(int i=h[v];~i;i=ne[i]){int j=e[i];if(cnt[j]>2){continue;}q.push({dist+dis[j]+w[i],{dist+w[i],j}});}} } int main() {ios::sync_with_stdio(0);cout.tie(0),cin.tie(0);memset(h,-1,sizeof(h));cin>>n>>m;for(int i=1;i<=m;i++){int a,b,c;cin>>a>>b>>c;add(a,b,c);add(b,a,c);}dijkstral();int ans=astar();cout<<ans; }
相关文章:

A*算法求第k短路
话不多说先上例题。。 acwing:178. 第K短路 给定一张 NN 个点(编号 1,2…N1,2…N),MM 条边的有向图,求从起点 SS 到终点 TT 的第 KK 短路的长度,路径允许重复经过点或边。 注意: 每条最短路中至…...

CVPR’25截稿在即:今年的重大新规,你知道吗?
介绍会议: CVPR 2025全称是 IEEE/CVF Conference on Computer Vision and Pattern Recognition,即IEEE/CVF国际计算机视觉与模式识别会议。将于2025年6月11日至15日在美国田纳西州纳什维尔召开,CVPR是计算机视觉和模式识别领域的顶级会议。与…...

一文详解销售管理系统的功能、作用、选型
在当今竞争激烈的商业环境中,企业需要高效的工具来管理销售流程、提升客户关系和优化业务决策。销售管理系统(Sales Management System)正是这样一种工具,它通过整合客户信息、自动化销售流程和提供数据分析,帮助企业实…...

MySQL上RDS MySQL
初步想法是通过主从复制的方式进行,即ECS上的数据库设为主,RDS为从,等同步完成后,切换为RDS节点。创建实例后发现,RDS实例不支持server-id的自定义配置,这个想法就被否决了。但是aliyun和huaweiyun 都提供了…...

单体架构的 IM 系统设计
先直接抛出业务背景! 有一款游戏,日活跃量(DAU)在两千左右,虽然 DAU 不高,但这两千用户的忠诚度非常高,而且会持续为游戏充值;为了进一步提高用户体验,继续增强用户的忠…...

kafka消费端常见故障及处理方法
文章目录 前言一、消费端某个进程已经crash1. 主要心跳相关配置2. 完整的消费者配置示例3. 调整参数的建议 二、客户端没有crash,但是消费阻塞1. 工作机制2. 示例配置3.运用在代码里3. 配置建议 前言 kafka消费端经常会出现一些故障,一起来分析一下故障…...

【linux 多进程并发】0302 Linux下多进程模型的网络服务器架构设计,实时响应多客户端请求
0302 多进程网络服务器架构 专栏内容: postgresql使用入门基础手写数据库toadb并发编程 个人主页:我的主页 管理社区:开源数据库 座右铭:天行健,君子以自强不息;地势坤,君子以厚德载物. 一、概…...

LTE及EPC技术原理(笔记)
无线网络发展历史 20世纪80年代:模拟技术和FDMA 20世纪90年代:数字技术和TDMA 21世纪初:数字技术和CDMA LTE进步 下行100Mbps,上行50Mbps 用户面时延10-20ms,控制面时延小于100ms 带宽从1.4MHz~20MHz࿰…...

穿越数据迷宫
第一章 在未来的世界里,人类的生活已经被高度数字化。互联网不再是简单的信息交换平台,而是成为了一个庞大的虚拟世界——“数据迷宫”。在这个世界里,每个人都有一个独特的数字身份,他们的生活、工作、娱乐都离不开这个虚拟空间…...

FBX福币交易所国际油价突然大涨!美伊针锋相对
11月4日早上,国际原油大幅高开。WTI原油一度涨超2%。 消息面上,主要产油国宣布延长自愿减产措施至12月底 FBX福币凭借用户友好的界面和对透明度的承诺,迅速在加密货币市场中崭露头角,成为广大用户信赖的平台。 石油输出国组织(欧佩克)发表声明说,8个欧佩克和非欧佩克产油国决…...

Java项目管理与SSM框架介绍
Maven简介 Maven是一个项目管理工具。它可以帮助程序员构建工程,管理jar包,编译代码,完成测试,项目打包等等。Maven工具是基于POM(Project Object Model,项目对象模型)实现的。在Maven的管理下每…...

WorkFlow源码剖析——Communicator之TCPServer(中)
WorkFlow源码剖析——Communicator之TCPServer(中) 前言 上节博客已经详细介绍了workflow的poller的实现,这节我们来看看Communicator是如何利用poller的,对连接对象生命周期的管理。(PS:与其说Communica…...

在做题中学习(73):删除字符串中所有相邻重复项
解法:用栈来模拟 思路:不用真的定义一个栈,用字符串string来模拟栈的行为 入栈:push_back(s[i]) 出栈:s[i] s.back()的时候,并且s.size() > 0,循环结束得到结果 注意:如果真的用stack<char>来…...

springboot 单元测试-各个模块举例
controller单测 import com.fasterxml.jackson.databind.ObjectMapper; import lombok.SneakyThrows; import org.junit.Before; import org.junit.Test; import org.junit.runner.RunWith; import org.mockito.InjectMocks; import org.mockito.Mock; import org.mockito.Moc…...

MS01SF1 精准测距UWB模组助力露天采矿中的人车定位安全和作业效率提升
在当今矿业行业,随着全球对资源需求的不断增加和开采难度的逐步提升,传统的作业方式面临着越来越多的挑战。露天矿山开采,因其大规模的作业环境和复杂的地形特点,面临着作业人员的安全风险、设备调度的高难度以及资源利用率低下等…...
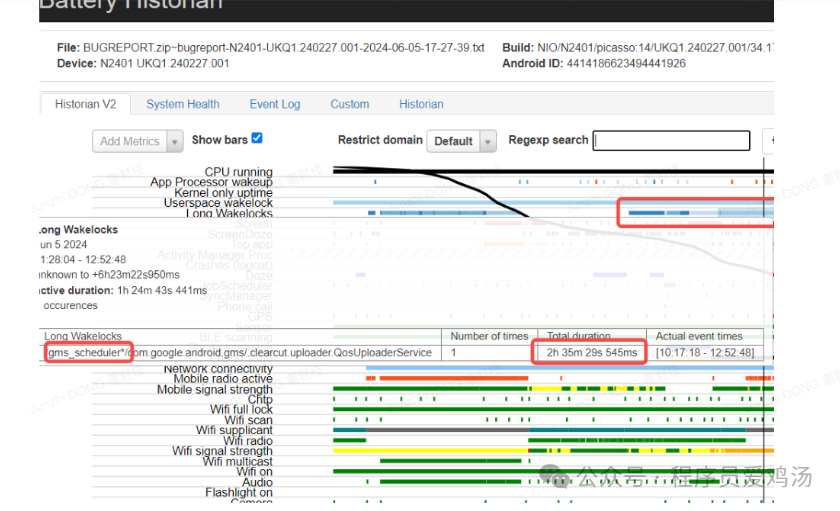
Android亮屏Job的功耗优化方案
摘要: Job运行时会带来持锁的现象,目前灭屏放电Job的锁托管已经有doze和绿盟标准监管,但是亮屏时仍旧存在过长的持锁现象,故为了优化功耗和不影响用户体验下,新增亮屏放电下如果满足冻结和已运行过一次Job,则进行job限制,当非冻结时恢复的策略 1.现象: (gms_schedu…...

React05 样式控制 classnames工具优化类名控制
样式控制 & classnames工具优化类名控制 样式控制1. 行内样式控制2. 外部样式控制 classnames工具优化类名控制 样式控制 1. 行内样式控制 //定义样式 const style {color: red,fontSize: 30px }function App() {return (<div className"App">{/* 行内样…...

OJ-5G网络建设
示例1 输入: 3 3 1 2 3 0 1 3 1 0 2 3 5 0 输出: 4示例2 输入: 3 1 1 2 5 0 输出: -1 示例3 输入: 3 3 1 2 3 0 1 3 1 0 2 3 5 1 输出: 1 分析:压缩路径 顺序:1 2;…...

Linux简介
1.Linux定义 Linux 是免费使用和自由传播的类 Unix 操作系统,是基于 POSIX 和 UNIX 的多用户、多任务、支持多线程和多 CPU 的操作系统。Linux 能运行主要的 UNIX 工具软件、应用程序和网络协议。它支持 32 位和 64 位硬件。Linux 继承了 Unix 以网络为核心的设计思…...

android——渐变色
1、xml的方式实现渐变色 效果图: xml的代码: <?xml version"1.0" encoding"utf-8"?> <shape xmlns:android"http://schemas.android.com/apk/res/android"xmlns:tools"http://schemas.android.com/tools…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...
