从最小作用量原理推导牛顿三大定律
从最小作用量原理推导牛顿三大定律
引言
在物理学中,牛顿三大定律是描述经典力学中物体运动的基本定律。然而,这些定律并不是孤立存在的,它们可以从一个更为普遍的原理——最小作用量原理中推导出来。最小作用量原理是一个深刻而优雅的理论,它指出物理系统的演化路径是使作用量达到极小值的路径。
本文的结构如下:首先,我们将介绍拉格朗日量的概念,并通过简单的例子帮助理解。接着,我们将详细解释最小作用量原理,并通过光的传播和物体的抛物线运动等例子来说明其应用。然后,我们会介绍变分法,这是推导欧拉-拉格朗日方程的数学工具。最后,我们将利用欧拉-拉格朗日方程推导出牛顿的三大定律。
通过这种结构,我们希望展示出最小作用量原理如何统一地解释经典力学中的基本定律,并揭示出自然界中运动的深层次规律。
拉格朗日量的直观理解
在开始之前,让我们先理解什么是拉格朗日量(Lagrangian)。拉格朗日量可以简单理解为系统"动能"和"势能"的差值:
L = T − V L = T - V L=T−V
其中 T T T 是动能, V V V 是势能。
让我们通过几个简单的例子来理解:
- 自由落体
想象你从高处扔下一个球。这个球有:
- 动能 T = 1 2 m v 2 T = \frac{1}{2}mv^2 T=21mv2(由运动产生)
- 势能 V = m g h V = mgh V=mgh(由高度产生)
所以它的拉格朗日量是:
L = 1 2 m v 2 − m g h L = \frac{1}{2}mv^2 - mgh L=21mv2−mgh
- 弹簧振动
想象一个弹簧上挂着的小球:
- 动能 T = 1 2 m v 2 T = \frac{1}{2}mv^2 T=21mv2(小球运动产生)
- 势能 V = 1 2 k x 2 V = \frac{1}{2}kx^2 V=21kx2(弹簧压缩或拉伸产生)
它的拉格朗日量是:
L = 1 2 m v 2 − 1 2 k x 2 L = \frac{1}{2}mv^2 - \frac{1}{2}kx^2 L=21mv2−21kx2
- 单摆
想象一个挂在绳子上摆动的小球:
- 动能 T = 1 2 m v 2 T = \frac{1}{2}mv^2 T=21mv2
- 势能 V = m g h = m g L ( 1 − cos θ ) V = mgh = mgL(1-\cos\theta) V=mgh=mgL(1−cosθ)(其中 L L L是绳长, θ \theta θ是摆角)
拉格朗日量为:
L = 1 2 m v 2 − m g L ( 1 − cos θ ) L = \frac{1}{2}mv^2 - mgL(1-\cos\theta) L=21mv2−mgL(1−cosθ)
拉格朗日量的物理意可以理解为系统的"活力":
- 动能代表系统的"运动活力"
- 势能代表系统的"储存活力"
- 它们的差值(拉格朗日量)描述了系统的总体状态
最小作用量原理简介
最小作用量原理是物理学中的一个重要概念,它告诉我们自然界中的物体总是沿着使某个量(称为“作用量”)最小的路径运动。这个原理可以帮助我们理解为什么物体会以某种方式运动。
作用量的定义
作用量 S S S 是一个物理量,它是拉格朗日量 L L L 在时间上的积分:
S = ∫ t 1 t 2 L d t S = \int_{t_1}^{t_2} L \, dt S=∫t1t2Ldt
其中, L L L 是拉格朗日量, t 1 t_1 t1 和 t 2 t_2 t2 分别是运动的起始时间和结束时间。
例子:光的最短路径
一个经典的例子是光的传播。光在两点之间传播时,总是选择最短的路径,这就是我们常说的“光走直线”。实际上,光选择的是使作用量最小的路径。
- 光在空气中传播:光在均匀介质中传播时,路径是一条直线,因为这条路径使作用量最小。
- 光在不同介质中传播:当光从空气进入水中时,它会发生折射。光的路径不再是直线,而是折射后的曲线。这是因为光在不同介质中传播时,速度不同,作用量的计算也不同。光选择的路径是使总作用量最小的路径。
例子:抛物线轨迹
想象一个物体在重力作用下从高处抛出。我们知道它的轨迹是一条抛物线。通过最小作用量原理,我们可以理解这条抛物线是物体选择的使作用量最小的路径。
- 动能和势能:物体的动能 T = 1 2 m v 2 T = \frac{1}{2}mv^2 T=21mv2,势能 V = m g h V = mgh V=mgh。
- 拉格朗日量: L = T − V = 1 2 m v 2 − m g h L = T - V = \frac{1}{2}mv^2 - mgh L=T−V=21mv2−mgh。
- 作用量: S = ∫ t 1 t 2 ( 1 2 m v 2 − m g h ) d t S = \int_{t_1}^{t_2} \left(\frac{1}{2}mv^2 - mgh\right) \, dt S=∫t1t2(21mv2−mgh)dt。
通过最小作用量原理,我们可以找到使得 S S S 最小的路径,这条路径就是物体的真实运动轨迹。
变分法基础
变分法是用来寻找某个量(通常是积分)达到极值的数学方法。在物理学中,我们用变分法来寻找使作用量 S S S 达到极值的路径。
变分法的基本思想
变分法的核心思想是:如果我们想要找到一个函数,使得某个积分(比如作用量)达到最小值,我们可以考虑对这个函数做微小的变化,然后观察积分的变化。
设想一条真实路径 x ( t ) x(t) x(t) 和一条微小偏离的路径 x ( t ) + δ x ( t ) x(t) + \delta x(t) x(t)+δx(t),其中 δ x ( t ) \delta x(t) δx(t) 是微小的变化。在路径的起点和终点,变化为零:
δ x ( t 1 ) = δ x ( t 2 ) = 0 \delta x(t_1) = \delta x(t_2) = 0 δx(t1)=δx(t2)=0
我们希望找到这样的路径,使得作用量 S S S 的变化 δ S \delta S δS 为零:
δ S = δ ∫ t 1 t 2 L ( x , x ˙ , t ) d t = 0 \delta S = \delta \int_{t_1}^{t_2} L(x, \dot{x}, t) \, dt = 0 δS=δ∫t1t2L(x,x˙,t)dt=0
例子:寻找最短路径
假设你在一个平面上有两点 A A A 和 B B B,你想找到从 A A A 到 B B B 的最短路径。直觉告诉我们,这条路径应该是一条直线。变分法就是用来证明这条直线确实是最短路径的方法。
- 路径的表示:假设路径用函数 y ( x ) y(x) y(x) 表示。
- 路径长度的积分:路径的长度可以表示为积分 ∫ x 1 x 2 1 + ( y ′ ) 2 d x \int_{x_1}^{x_2} \sqrt{1 + (y')^2} \, dx ∫x1x21+(y′)2dx,其中 y ′ = d y d x y' = \frac{dy}{dx} y′=dxdy。
- 变分法应用:通过对 y ( x ) y(x) y(x) 做微小变化 y ( x ) + δ y ( x ) y(x) + \delta y(x) y(x)+δy(x),并要求路径长度的变化为零,我们可以找到最短路径。
欧拉-拉格朗日方程的推导
考虑作用量的变分:
δ S = δ ∫ t 1 t 2 L ( x , x ˙ , t ) d t = 0 \delta S = \delta \int_{t_1}^{t_2} L(x, \dot{x}, t) \, dt = 0 δS=δ∫t1t2L(x,x˙,t)dt=0
展开变分:
δ S = ∫ t 1 t 2 ( ∂ L ∂ x δ x + ∂ L ∂ x ˙ δ x ˙ ) d t = 0 \delta S = \int_{t_1}^{t_2} \left( \frac{\partial L}{\partial x} \delta x + \frac{\partial L}{\partial \dot{x}} \delta \dot{x} \right) dt = 0 δS=∫t1t2(∂x∂Lδx+∂x˙∂Lδx˙)dt=0
注意到 δ x ˙ = d d t ( δ x ) \delta \dot{x} = \frac{d}{dt}(\delta x) δx˙=dtd(δx),对第二项进行分部积分:
∫ t 1 t 2 ∂ L ∂ x ˙ δ x ˙ d t = ∂ L ∂ x ˙ δ x ∣ t 1 t 2 − ∫ t 1 t 2 d d t ( ∂ L ∂ x ˙ ) δ x d t \int_{t_1}^{t_2} \frac{\partial L}{\partial \dot{x}} \delta \dot{x} \, dt = \left. \frac{\partial L}{\partial \dot{x}} \delta x \right|_{t_1}^{t_2} - \int_{t_1}^{t_2} \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right) \delta x \, dt ∫t1t2∂x˙∂Lδx˙dt=∂x˙∂Lδx t1t2−∫t1t2dtd(∂x˙∂L)δxdt
由于端点处 δ x = 0 \delta x = 0 δx=0,第一项消失。代回原式:
δ S = ∫ t 1 t 2 [ ∂ L ∂ x − d d t ( ∂ L ∂ x ˙ ) ] δ x d t = 0 \delta S = \int_{t_1}^{t_2} \left[ \frac{\partial L}{\partial x} - \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right) \right] \delta x \, dt = 0 δS=∫t1t2[∂x∂L−dtd(∂x˙∂L)]δxdt=0
由于 δ x \delta x δx 是任意的,根据变分法的基本引理,方括号中的式子必须为零:
d d t ( ∂ L ∂ x ˙ ) − ∂ L ∂ x = 0 \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right) - \frac{\partial L}{\partial x} = 0 dtd(∂x˙∂L)−∂x∂L=0
这就是著名的欧拉-拉格朗日方程。它是最小作用量原理的数学表达,也是我们推导牛顿运动定律的基础。
牛顿第一定律推导
牛顿第一定律(惯性定律)指出,如果一个物体不受外力作用,它将保持静止状态或匀速直线运动状态。我们可以利用前面推导的欧拉-拉格朗日方程来证明这一结论。
假设一个物体的拉格朗日量 L L L 仅依赖于位置 x x x 和速度 x ˙ \dot{x} x˙,且不受外力作用:
L = 1 2 m x ˙ 2 L = \frac{1}{2} m \dot{x}^2 L=21mx˙2
其中, m m m 是物体的质量。将此拉格朗日量代入前面推导的欧拉-拉格朗日方程:
d d t ( ∂ L ∂ x ˙ ) − ∂ L ∂ x = 0 \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right) - \frac{\partial L}{\partial x} = 0 dtd(∂x˙∂L)−∂x∂L=0
得到:
d d t ( m x ˙ ) = 0 \frac{d}{dt} (m \dot{x}) = 0 dtd(mx˙)=0
这意味着 m x ˙ m \dot{x} mx˙ 是一个常数,即物体的速度 x ˙ \dot{x} x˙ 保持不变。因此,如果物体不受外力作用,它将保持静止状态或匀速直线运动状态,这就是牛顿第一定律。
牛顿第二定律推导
牛顿第二定律(加速度定律)指出,物体的加速度与所受外力成正比,且加速度的方向与外力的方向相同。同样可以利用欧拉-拉格朗日方程来推导。
考虑包含势能的拉格朗日量:
L = 1 2 m x ˙ 2 − V ( x ) L = \frac{1}{2} m \dot{x}^2 - V(x) L=21mx˙2−V(x)
其中, V ( x ) V(x) V(x) 是势能,满足 F = − d V d x F = -\frac{dV}{dx} F=−dxdV。将此拉格朗日量代入欧拉-拉格朗日方程:
d d t ( ∂ L ∂ x ˙ ) − ∂ L ∂ x = 0 \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right) - \frac{\partial L}{\partial x} = 0 dtd(∂x˙∂L)−∂x∂L=0
得到:
d d t ( m x ˙ ) + d V d x = 0 \frac{d}{dt} (m \dot{x}) + \frac{dV}{dx} = 0 dtd(mx˙)+dxdV=0
由于 F = − d V d x F = -\frac{dV}{dx} F=−dxdV,可以得到牛顿第二定律:
m x ¨ = F m \ddot{x} = F mx¨=F
牛顿第三定律推导
牛顿第三定律(作用与反作用定律)同样可以通过欧拉-拉格朗日方程推导。考虑两个相互作用物体的拉格朗日量:
L = 1 2 m 1 x ˙ 1 2 + 1 2 m 2 x ˙ 2 2 − V ( x 1 , x 2 ) L = \frac{1}{2} m_1 \dot{x}_1^2 + \frac{1}{2} m_2 \dot{x}_2^2 - V(x_1, x_2) L=21m1x˙12+21m2x˙22−V(x1,x2)
对两个坐标分别应用欧拉-拉格朗日方程:
d d t ( ∂ L ∂ x ˙ i ) − ∂ L ∂ x i = 0 , i = 1 , 2 \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}_i}\right) - \frac{\partial L}{\partial x_i} = 0, \quad i = 1,2 dtd(∂x˙i∂L)−∂xi∂L=0,i=1,2
得到:
m 1 x ¨ 1 = − ∂ V ∂ x 1 = F 12 m_1 \ddot{x}_1 = -\frac{\partial V}{\partial x_1} = F_{12} m1x¨1=−∂x1∂V=F12
m 2 x ¨ 2 = − ∂ V ∂ x 2 = F 21 m_2 \ddot{x}_2 = -\frac{\partial V}{\partial x_2} = F_{21} m2x¨2=−∂x2∂V=F21
由于势能 V ( x 1 , x 2 ) V(x_1, x_2) V(x1,x2) 的对称性,可以证明 F 12 = − F 21 F_{12} = -F_{21} F12=−F21,这就是牛顿第三定律。
总结与展望
通过本文的推导,我们展示了如何从最小作用量原理出发,利用拉格朗日量和变分法,推导出经典力学中牛顿的三大定律。这一过程不仅揭示了牛顿定律背后的深层次原理,也展示了物理学中不同理论之间的内在联系。
最小作用量原理作为一个普遍的物理原理,不仅适用于经典力学,还在量子力学、相对论和场论中发挥着重要作用。它为我们提供了一种统一的视角来理解自然界的规律。
相关文章:

从最小作用量原理推导牛顿三大定律
从最小作用量原理推导牛顿三大定律 引言 在物理学中,牛顿三大定律是描述经典力学中物体运动的基本定律。然而,这些定律并不是孤立存在的,它们可以从一个更为普遍的原理——最小作用量原理中推导出来。最小作用量原理是一个深刻而优雅的理论…...

【系统集成项目管理工程师教程】第4章 信息系统架构
教程内容总结,供参考,有错误请指正,友好交流。 4.架构基础 4.1.1指导思想 4.1.2设计原则 原则内容:包括坚持以人为本、创新引领、问题导向、整体协同、安全可控、科学实施等,这些原则应基于组织的信念和价值观&…...
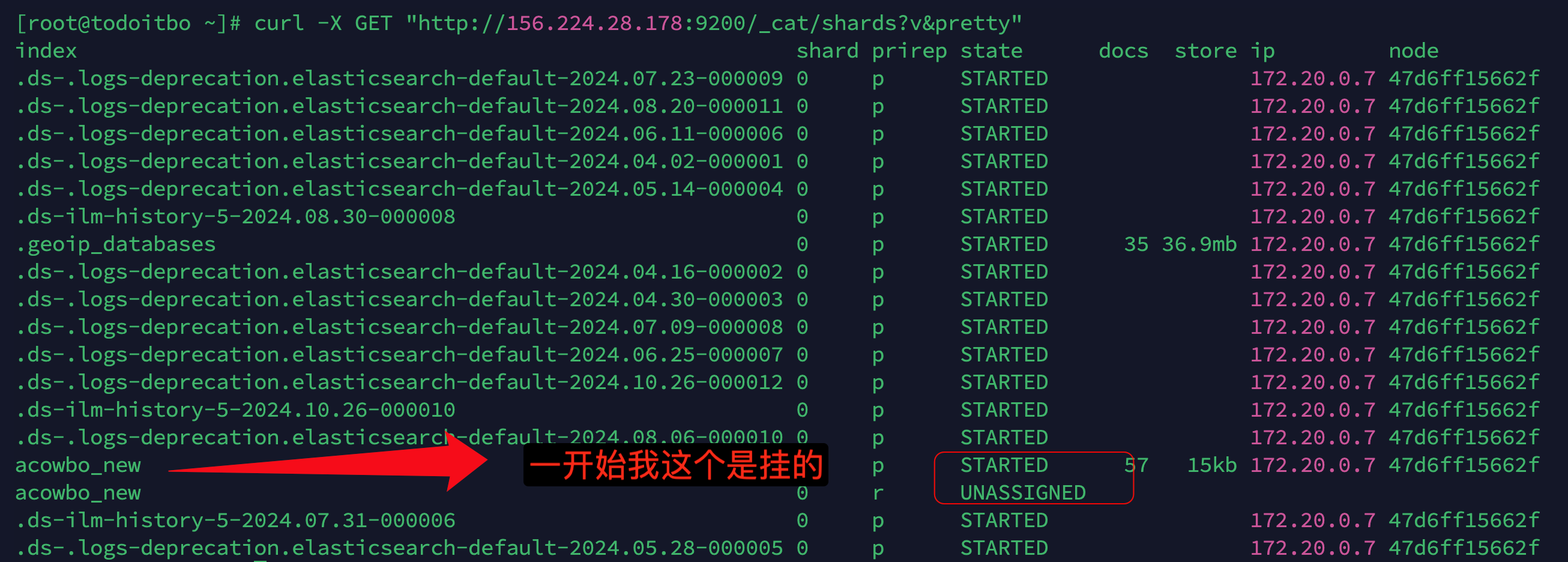
docker下迁移elasticsearch的问题与解决方案
欢迎来到我的博客,代码的世界里,每一行都是一个故事 🎏:你只管努力,剩下的交给时间 🏠 :小破站 docker下迁移elasticsearch的问题与解决方案 数据挂载报错解决权限问题节点故障 直接上图&#x…...

占地1.1万平,2亿投资的智能仓储系统:高架库、AGV、码垛机器人……
导语 大家好,我是社长,老K。专注分享智能制造和智能仓储物流等内容。 我国调味料市场近年来展现出惊人的增长潜力,各大品牌纷纷加大投入,力求在竞争中脱颖而出。 广东美味鲜调味食品有限公司,作为行业内的佼佼者&#…...

一个小程序如何对接多个收款账户?
背景 我又来了,之前对接过网约巴士系统 网约巴士旅游专线平台搭建历程,运营了两年多了。在运营中完善、在完善中学习,一直是不变的真理。有一句话说得好:先做一个垃圾、用起来再说。 今天又需要升级了,需求是&#…...

L2G4000 InternVL 部署微调实践闯关任务
一、理解多模态大模型的常见设计模式,可以大概讲出多模态大模型的工作原理。 视频地址 开源的多模态大模型:InternVL,Qwen-VL,LLaVA 闭源的:GPT-4o 研究重点:不同模态特征空间的对齐 BLIP2 将图像特征对…...

asynDriver-6-端口驱动
本地串口 drvAsynSerialPort驱动支持设备连接到IOC上串口。 用drvAsynSerialPortConfigure和asynSetOption命令配置串口: drvAsynSerialPortConfigure("portName","ttyName",priority,noAutoConnect,noProcessEosIn) asynSetOption("po…...

[免费]基于Python的Django+Vue3在线考试系统【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的基于Python的DjangoVue3在线考试系统,分享下哈。 项目视频演示 【免费】基于Python的DjangoVue3在线考试系统 Python毕业设计_哔哩哔哩_bilibili 项目介绍 本论文提出并实现了一种基于Python…...

Python使用爬虫
一、基本介绍 爬虫(Web Scraping)是一种自动化获取网页内容的技术,它通过编写程序模拟浏览器的行为,从互联网上抓取网页数据。爬虫可以用于多种目的,比如数据收集、信息整合、自动化测试等。 二、常用的库 1、Request…...

CommunityToolkit.Mvvm如何使用
CommunityToolkit.Mvvm 是一个现代、快速和模块化的 MVVM 库,用于 .NET 应用程序。以下是如何使用 CommunityToolkit.Mvvm 的基本步骤: 安装包: 你可以通过 NuGet 包管理器安装 CommunityToolkit.Mvvm。在 Visual Studio 中,你可以…...
Python小游戏20——超级玛丽
首先,你需要确保你的Python环境中安装了pygame库。如果还没有安装,可以使用以下命令进行安装: bash pip install pygame 运行效果展示 代码展示 python import pygame import sys # 初始化pygame pygame.init() # 设置屏幕尺寸 screen_width …...
)
配置文件格式(xml、properties、yml/yaml)
配置文件格式(xml、properties、yml/yaml) 配置文件格式一、XML二、properties三、yml/yaml基本语法yml数据格式1、对象/Map集合1、数组/List/Set集合 配置文件格式 什么是配置文件?: 配置文件是包含应用程序或系统配置信息的文件…...

CentOS 7 软件/程序安装示例
安装软件/程序 wget,前提需要用 root 用户 1、搜索软件/程序 yum search wget 搜索到软件/程序。 2、安装软件/程序 yum -y install wget 安装完成。...

Python绘制正弦函数图形
1,绘制正弦函数图形,让数学看得见, import math # 导入函数模块 import turtle # 导入turtle模块,用于绘图t turtle.Turtle() # 创建对象 turtle.bgcolor("#2dded9") # 设置背景颜色 t.pencolor(blue) # 设置画笔…...

【LVGL-列表部件 lv_list_create】
LVGL-列表部件 lv_list_create ■ LVGL-列表部件-函数■ 修改样式-■ 修改样式- 背景色■ 修改样式- 改变项的颜色-label■ 修改样式- 改变项的颜色-btn ■ 事件(Event)■ 示例0:综合■ 示例1(自动出现滚动)■ 示例2(滚动捕捉&…...

【P2-6】ESP8266 WIFI模块在STA模式下实现UDP与电脑/手机网络助手通信——UDP数据透传
前言:完成ESP8266 WIFI模块在STA模式下实现UDP与电脑/手机网络助手通信——实现UDP数据透传 STA模式,通俗来说就是模块/单片机去连接路由器/热点来通信。 UDP协议,是传输层协议,UDP没有服务器和客户端的说法。 本实验需要注意,wifi模块/单片机与电脑/手机需要连接在同一个…...
-----剪枝基本概念)
从零学习大模型(十)-----剪枝基本概念
剪枝的基本概念 模型压缩中的地位:剪枝是模型压缩中的重要技术之一,它通过减少模型的参数量来降低计算资源的需求。对于大型神经网络,尤其是像BERT、GPT等参数量级巨大的模型,剪枝可以有效地减少模型的内存占用和计算量ÿ…...

Jest进阶知识:模拟 ES6 类 - 掌握类的依赖模拟与方法监听技巧
引言 在现代前端开发中,ES6 类(class)是常用的一种面向对象编程方式。在测试类的时候,我们经常需要模拟类的依赖,以避免外部因素对测试结果的影响。Jest 提供了强大的工具来模拟类及其方法,确保测试的高效…...

前端Nginx的安装与应用
目录 一、前端跨域方式 1.1、CORS(跨域资源共享) 1.2、JSONP(已过时) 1.3、WebSocket 1.4、PostMessage 1.5、Nginx 二、安装 三、应用 四、命令 4.1、基本操作命令 4.2、nginx.conf介绍 4.2.1、location模块 4.2.2、反向代理配置 4.2.3、负载均衡模块 4.2.4、通…...

Java设计模式(代理模式整理中ing)
一、代理模式 1、代理模式定义: 代理模式:由于某些原因要给某对象提供一个代理以控制对该对象的访问,这时访问对象不适合或者不能够直接引用目标对象,代理对象作为访问对象与目标对象之间的中介进行连接调控调用。 2、代理模式的…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...
