贝尔不等式的验证
在量子计算机上运行一个实验,以演示使用Estimator原型违反CHSH不等式。
import numpy as npfrom qiskit import QuantumCircuit
from qiskit.circuit import Parameter
from qiskit.quantum_info import SparsePauliOpfrom qiskit_ibm_runtime import QiskitRuntimeService
from qiskit_ibm_runtime import EstimatorV2 as Estimatorimport matplotlib.pyplot as plt
import matplotlib.ticker as tck#要在硬件上运行,请选择队列中作业数量最少的后端
service = QiskitRuntimeService(channel="ibm_quantum")
backend = service.least_busy(operational=True, simulator=False, min_num_qubits=127)
backend.name创建一个参数化的CHSH电路
首先,我们用参数θ来编写电路,我们称之为θ。Estimator原型机通过直接提供可观测值的期望值,极大地简化了电路的构建和输出分析。许多令人感兴趣的问题,特别是对于噪声系统的近期应用,都可以用期望值来表示。估计器(V2)原语可以根据提供的可观察对象自动更改度量基础。
theta = Parameter("$\\theta$")chsh_circuit = QuantumCircuit(2)
chsh_circuit.h(0)
chsh_circuit.cx(0, 1)
chsh_circuit.ry(theta, 0)
chsh_circuit.draw(output="mpl", idle_wires=False, style="iqp") 
创建参数化CHSH电路后,下一步将创建要分配给电路的相位值列表。您可以使用以下代码创建21个相位值的列表,范围从0到2π,间距相等,即0 0,0.1π,0.2π,…,1.9π, 2π。
number_of_phases = 21
phases = np.linspace(0, 2 * np.pi, number_of_phases)
# Phases need to be expressed as list of lists in order to work
individual_phases = [[ph] for ph in phases]现在我们需要计算期望值的可观察对象。在我们的例子中,我们正在查看每个量子位的正交基,让第一个量子位的参数化- Y -旋转相对于第二个量子位基几乎连续地扫描测量基。因此,我们将选择可观测值ZZ、ZX、XZ和XX。
# <CHSH1> = <AB> - <Ab> + <aB> + <ab> -> <ZZ> - <ZX> + <XZ> + <XX>
observable1 = SparsePauliOp.from_list([("ZZ", 1), ("ZX", -1), ("XZ", 1), ("XX", 1)])# <CHSH2> = <AB> + <Ab> - <aB> + <ab> -> <ZZ> + <ZX> - <XZ> + <XX>
observable2 = SparsePauliOp.from_list([("ZZ", 1), ("ZX", 1), ("XZ", -1), ("XX", 1)])from qiskit.transpiler.preset_passmanagers import generate_preset_pass_managertarget = backend.target
pm = generate_preset_pass_manager(target=target, optimization_level=3)chsh_isa_circuit = pm.run(chsh_circuit)
chsh_isa_circuit.draw(output="mpl", idle_wires=False, style="iqp")isa_observable1 = observable1.apply_layout(layout=chsh_isa_circuit.layout)
isa_observable2 = observable2.apply_layout(layout=chsh_isa_circuit.layout)为了在对Estimator的一次调用中执行整个实验。我们可以创建一个Qiskit Runtime Estimator原型机来计算我们的期望值。EstimatorV2.run()方法接受一个原始统一块(pub)的可迭代对象。每个PUB都是一个可迭代对象,格式为(circuit, observables, parameter_values: Optional, precision: Optional)
# To run on a local simulator:
# Use the StatevectorEstimator from qiskit.primitives instead.estimator = Estimator(mode=backend)pub = (chsh_isa_circuit, # ISA circuit[[isa_observable1], [isa_observable2]], # ISA Observablesindividual_phases, # Parameter values
)job_result = estimator.run(pubs=[pub]).result()chsh1_est = job_result[0].data.evs[0]
chsh2_est = job_result[0].data.evs[1]fig, ax = plt.subplots(figsize=(10, 6))# results from hardware
ax.plot(phases / np.pi, chsh1_est, "o-", label="CHSH1", zorder=3)
ax.plot(phases / np.pi, chsh2_est, "o-", label="CHSH2", zorder=3)# classical bound +-2
ax.axhline(y=2, color="0.9", linestyle="--")
ax.axhline(y=-2, color="0.9", linestyle="--")# quantum bound, +-2√2
ax.axhline(y=np.sqrt(2) * 2, color="0.9", linestyle="-.")
ax.axhline(y=-np.sqrt(2) * 2, color="0.9", linestyle="-.")
ax.fill_between(phases / np.pi, 2, 2 * np.sqrt(2), color="0.6", alpha=0.7)
ax.fill_between(phases / np.pi, -2, -2 * np.sqrt(2), color="0.6", alpha=0.7)# set x tick labels to the unit of pi
ax.xaxis.set_major_formatter(tck.FormatStrFormatter("%g $\\pi$"))
ax.xaxis.set_major_locator(tck.MultipleLocator(base=0.5))# set labels, and legend
plt.xlabel("Theta")
plt.ylabel("CHSH witness")
plt.legend()
plt.show()
参考:CHSH Inequality | IBM Quantum Learning
相关文章:

贝尔不等式的验证
在量子计算机上运行一个实验,以演示使用Estimator原型违反CHSH不等式。 import numpy as npfrom qiskit import QuantumCircuit from qiskit.circuit import Parameter from qiskit.quantum_info import SparsePauliOpfrom qiskit_ibm_runtime import QiskitRuntim…...

GR2——在大规模视频数据集上预训练且机器人数据上微调,随后预测动作轨迹和视频(含GR1详解)
前言 上个月的24年10.9日,我在朋友圈看到字节发了个机器人大模型GR2,立马去看了下其论文(当然了,本质是个技术报告) 那天之后,我就一直想解读这个GR2来着 然,意外来了,如此文《OmniH2O——通用灵巧且可全…...

伦敦金价格是交易所公布的吗?
今年以来,伦敦金价格波动可谓是波澜壮阔,盘中屡次刷新历史新高,目前已经冲上了2700的历史大关。面对高歌猛进的伦敦金价格,投资者除了进行交易之外,还有一点相关方面的知识是想了解的。例如,伦敦金价格是交…...

Oracle SQL Loader概念及用法
Oracle SQLLoader是Oracle数据库提供的一个高效的数据加载工具,它能够将外部数据(如CSV、DAT、Text等文件格式)快速加载到Oracle数据库中。以下是对Oracle SQLLoader的详细介绍: 一、主要功能 数据迁移:SQL*Loader常…...

ReactPress 是什么?
ReactPress Github项目地址:https://github.com/fecommunity/reactpress 欢迎Star。 ReactPress 是什么? ReactPress 是使用React开发的开源发布平台,用户可以在支持React和MySQL数据库的服务器上架设属于自己的博客、网站。也可以把 ReactP…...

MR30分布式IO模块与高效PLC协同
在现代工业自动化领域中,数据采集与控制系统扮演着至关重要的角色。其中,可编程逻辑控制器(PLC)和分布式IO模块(Distributed I/O Modules)是这一领域的两大核心组件。本文将详细介绍MR30分布式IO模块与PLC如…...

成都睿明智科技有限公司共赴抖音电商蓝海
在这个短视频风起云涌的时代,抖音作为现象级的社交媒体平台,不仅改变了人们的娱乐方式,更悄然间重塑了电商行业的格局。在这片充满机遇与挑战的蓝海中,成都睿明智科技有限公司凭借其敏锐的市场洞察力和专业的服务能力,…...

Android15音频进阶之音频策略加载及使用(九十一)
简介: CSDN博客专家、《Android系统多媒体进阶实战》一书作者 新书发布:《Android系统多媒体进阶实战》🚀 优质专栏: Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏: 多媒体系统工程师系列【原创干货持续更新中……】🚀 优质视频课程:AAOS车载系统+…...

Spring设值注入
设值注入(Setter Injection)是Spring框架中依赖注入的一种方式,通过Setter方法将依赖对象注入到目标对象中。设值注入在对象创建后,通过调用Setter方法完成依赖注入。 设值注入的优点 灵活性:设值注入允许在对象创建…...

Spring整合Mybatis过程
配置文件 springConfig --> [jdbcConfig mybatisConfig] jdbc配置文件进行基本的数据库连接池配置 mybatis配置文件进行SqlSessionFactory Bean 和 MapperScannerConfigurer Bean的创建 在Spring容器启动时,系统会根据配置创建并初始化所有MyBatis所需的Bean…...

常见HR问题篇
系列文章目录 第一章 C/C语言篇第二章 计算机网络篇第三章 操作系统篇第四章 数据库MySQL篇第五章 数据库Redis篇第六章 场景题/算法题第七篇 常见HR问题篇 本系列专栏:点击进入 后端开发面经 关注走一波 秋招阶段,面过很多大中小厂,积攒了…...
)
调用数据集mnist(下载+调用全攻略)
1、下载mnist数据集请自取: 通过百度网盘分享的文件:mnist 链接:https://pan.baidu.com/s/1ia3vFA73hEtWK9qU-O-4iQ?pwdmnis 提取码:mnis 下载后把数据集放在没有中文的路径下。 # 本文将下载好的数据集放在C:\DeepLearning\…...
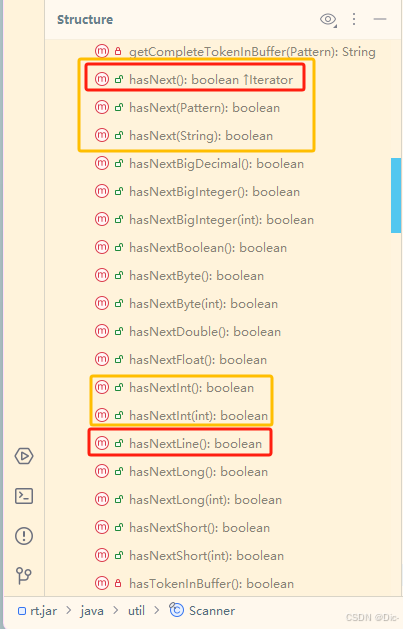
【基础语法】Java Scanner hasNext() 和 hasNextLine() 的区别
OJ在线编程常见输入输出练习中默认模板 import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息 public class Main {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.…...

react使用Fullcalendar 实战用法
使用步骤请参考:react使用Fullcalendar 卡片式的日历: 需求图: 卡片式的日历,其实我是推荐 antd的,我两个都写了一下都能实现。 antd 的代码: antd的我直接用的官网示例:antd 日历示例 i…...
优秀项目经理必知的10款项目管理软件推荐
本文精心为项目经理推荐30款国内外免费的项目管理软件,涵盖桌面应用与Web平台,其中不乏优秀的开源软件。这些工具旨在助力项目经理高效规划、跟踪与控制项目,无论是通过甘特图进行可视化管理,还是利用任务分配、团队协作等功能&am…...

植物神经紊乱不用怕,这些维生素来帮你!
你是否经常感到身体疲惫、情绪波动大、心悸、胸闷?这可能是植物神经紊乱在作祟。别担心,通过合理的维生素补充,可以有效缓解症状,提升生活质量。今天,我们就来聊聊植物神经紊乱患者应该补充哪些维生素。 🔍…...

NRF52832学习笔记(41)——添加串口库libuarte
一、背景 由于板子上不支持硬件流控,在使用 app_uart_fifo 库接收串口大数据时,频繁报 APP_UART_COMMUNICATION_ERROR 错误,多次重新初始化后,串口也不再产生中断了。查看官方论坛后决定使用串口异步库 libuarte。 二、简介 Li…...

Moore Perf System 1.1版本
Moore Perf System(一款性能分析工具) 提供可视化界面,在时间轴上按时间顺序显示 CPU 和 GPU 的事件、吞吐和性能指标,帮助开发人员方便、快速、准确的定位到系统级别的性能瓶颈,进而进行针对性分析和优化,…...

SpringBoot+Shirp的权限管理
目录 怎么实现动态菜单 1.html页面 2.获取动态菜单 Shiro权限刷新 1. 配置Shiro 2. 创建权限刷新服务 3. 调用权限刷新服务 注意事项 如何更新ShiroFilter初始权限 怎么实现动态菜单 1.html页面 <ul class"nav side-menu"><!--第一重循环…...

OpenCV图像基础
目录 显示窗口 创建空白图像 保存图片 图像裁剪 调整图片大小 图像绘制 绘制圆形 绘制矩形 绘制直线 绘制文本 中文乱码 控制鼠标 视频处理 显示窗口 cv2.namedWindow(winname, flagsNone) 创建一个命名窗口,以便在该窗口中显示图像或进行其他图形操作…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...
