动态规划 —— dp问题-按摩师
1. 按摩师
题目链接:
面试题 17.16. 按摩师 - 力扣(LeetCode)
https://leetcode.cn/problems/the-masseuse-lcci/description/

2. 算法原理
状态表示:以某一个位置为结尾或者以某一个位置为起点
dp[i]表示:选择到i位置的时候,此时的最长预约时长分两种情况:
1.f[i]表示:选择到i位置的时候,当前位置nums[i]必选,此时的最长预约时长
2.g[i]表示:选择到i位置的时候,当前位置nums[i]不选,此时的最长预约时长
2. 状态转移方程
根据最近的一步来划分问题:
到达dp[i][j]有两种情况:
1. f[i]=g[i-1] + nums[i]
2. g[i]:a. 当选择i-1的位置时:f[i-1]
b.当不选择i-1的位置时:g[i-1]
g[i]=max(f[i-1],g[i-1])
3. 初始化 :把dp表填满不越界,让后面的填表可以顺利进行
本题初始化为:f[0]=nums[0] g[0]在vector填表的时候默认为0
4. 填表顺序
本题的填表顺序是:从左往右,两个表一起填
5. 返回值 :题目要求 + 状态表示
本题的返回值是:max(f[n-1],g[n-1])
3.代码
动态规划的固定四步骤:1. 创建一个dp表
2. 在填表之前初始化
3. 填表(填表方法:状态转移方程)
4. 确定返回值
class Solution {
public:int massage(vector<int>& nums) {int n=nums.size();//处理一下边界情况if(n==0) return 0;vector<int>f(n);auto g=f;f[0]=nums[0];for(int i=1;i<n;i++){f[i]=g[i-1]+nums[i];g[i]=max(f[i-1],g[i-1]);}return max(f[n-1],g[n-1]);}
};完结撒花~
相关文章:

动态规划 —— dp问题-按摩师
1. 按摩师 题目链接: 面试题 17.16. 按摩师 - 力扣(LeetCode)https://leetcode.cn/problems/the-masseuse-lcci/description/ 2. 算法原理 状态表示:以某一个位置为结尾或者以某一个位置为起点 dp[i]表示:选择到i位置…...

SQL 语法学习
在当今数字化的时代,数据的管理和分析变得至关重要。而 SQL(Structured Query Language),即结构化查询语言,作为一种用于管理关系型数据库的强大工具,掌握它对于从事数据相关工作的人来说是一项必备技能。在…...

MYSQL---TEST5(Trigger触发器Procedure存储过程综合练习)
触发器Trigger 数据库mydb16_trigger创建 表的创建 goods create table goods( gid char(8) primary key, #商品号 name varchar(10), #商品名 price decimal(8,2), #价格 num int;) #数量orders create tabl…...

蓝桥杯 区间移位--二分、枚举
题目 代码 #include <stdio.h> #include <string.h> #include <vector> #include <algorithm> #include <iostream> using namespace std; struct node{ int a,b; }; vector<node> q; bool cmp(node x,node y){ return x.b <…...

Nginx 报错400 Request Header Or Cookie Too Large
错误的原因: 1、可能是你的网络DNS配置错误。 2、由request header过大所引起,request过大,通常是由于cookie中写入了较大的值所引起的。 3、访问太频繁,浏览器的缓存量太大,产生错误。 解决办法: 1、清…...

【Redis】一种常见的Redis分布式锁原理简述
本文主要简述一下基于set命令的Redis分布式锁的原理。 一,a线程持有的锁不要被b线程同时持有→setnx 抢锁的时候,最核心的就是,a线程持有的锁不要被b线程同时持有,放在基于set命令的redis分布式锁中来看,就是“如果锁…...

HOT100_最大子数组和
class Solution {public int maxSubArray(int[] nums) {int[] dp new int[nums.length];int res nums[0];dp[0] nums[0];for(int i 1; i< nums.length; i){dp[i] Math.max(nums[i] ,dp[i-1] nums[i]);res Math.max(res, dp[i]);}return res;} }...

DiskGenius工具扩容Mac OS X Apple APFS分区
DiskGenius是一款功能强大的磁盘分区工具,它支持Windows和Mac OS X系统,可以用于管理硬盘分区,包括扩容Mac OS X的Apple APFS分区。然而,直接使用DiskGenius来扩容Mac OS X的APFS分区可能存在一定的风险,因为不是专门为…...

从零开始的LeetCode刷题日记:70. 爬楼梯
一.相关链接 题目链接:70. 爬楼梯 二.心得体会 这道题还是动规五部曲。 1.首先是dp数组及其下标的含义,dp记录了每层楼梯对应的爬的方法,每个下标存储每个对应楼层。 2.然后是递归公式,其实每一层楼都是可以从下面一层和下面…...

Unity照片墙效果
Unity照片墙效果,如下效果展示 。 工程源码...
【自动化利器】12个评估大语言模型(LLM)质量的自动化框架
LLM评估是指在人工智能系统中评估和改进语言和语言模型的过程。在人工智能领域,特别是在自然语言处理(NLP)及相关领域,LLM评估具有至高无上的地位。通过评估语言生成和理解模型,LLM评估有助于细化人工智能驱动的语言相…...

【1】基础概念
文章目录 一、特点二、基础语法注意三、官方编程指南四、go 语言标准库 API 一、特点 golang 一个 go 文件都要归属到一个包,需要进行申明。天然的并发:golang 从语言层面支持大并发。每个 go 文件都必须要归属到一个包中。执行 go 文件:go …...

HTML 文档规范与解析模式:DOCTYPE、<html> 标签以及结构化页面
文章目录 `<!DOCTYPE html>` 文档类型声明标准模式与怪异模式HTML5 的简化声明`<html>` 标签`<head>` 标签`<body>` 标签小结<!DOCTYPE html> 文档类型声明 在 HTML 文档中,<!DOCTYPE html> 是一个重要的文档类型声明,主要用于告知浏览…...

大模型微调技术 --> 脉络
Step1:脉络 微调技术从最早期的全模型微调演变成如今的各种参数高效微调(PEFT)方法,背后是为了应对大模型中的计算、存储和数据适应性的挑战 1.为什么有微调? 深度学习模型越来越大,尤其是 NLP 中的预训练语言模型(BERT, GPT)系列。如果从…...

不要只知道deepl翻译,这里有10个专业好用的翻译工具等着你。
deepl翻译的优点还是有很多的,比如翻译的准确性很高,支持翻译的语言有很多,并且支持翻译文件和文本。但是现在翻译工具那么多,大家需要翻译的场景也有很多,怎么能只拥有一个翻译工具呢。所以在这里我帮助大家寻找了一波…...
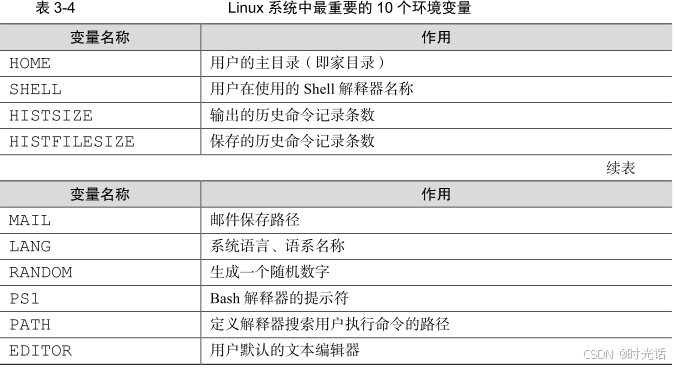
第二节 管道符、重定向与环境变量
1.重定向技术的 5 种模式 (1)标准覆盖输出重定向 (2)标准追加输出重定向 (3)错误覆盖输出重定向 (4)错误追加输出重定向 (5)输入重定向2.输入输出重定向 输入…...

Linux 服务器使用指南:从入门到登录
🌟快来参与讨论💬,点赞👍、收藏⭐、分享📤,共创活力社区。 🌟 🚩博主致力于用通俗易懂且不失专业性的文字,讲解计算机领域那些看似枯燥的知识点🚩 目录 一…...

QT 如何使QLabel的文字垂直显示
想要实现QLabel文字的垂直显示,可以通过使用“文字分割填充换行符”的方式来实现QLabel文字垂直显示的效果,下面是效果图: 具体实现代码: #include "mainwindow.h" #include "ui_mainwindow.h"MainWindow:…...

蓬勃发展:移动开发——关于软件开发你需要知道些什么
一、前言 移动开发一直都是软件开发领域中最有趣的领域之一,这是因为: 1、移动开发为“只有一个人”的开发团队提供了一个非常独特的机会,让他可以在相对较短的时间内建立一个实际的、可用的、有意义的应用程序; 2、移动开发也代…...

1095. 山脉数组中查找目标值
目录 题目解法lambda在这是怎么用的? 题目 (这是一个 交互式问题 ) 你可以将一个数组 arr 称为 山脉数组 当且仅当: arr.length > 3 存在一些 0 < i < arr.length - 1 的 i 使得: arr[0] < arr[1] <…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...


