triangle_area_calculators库发布
最近将在pip网站上发布triangle_area_calculators库(我编写的python第三方库)
triangle_area_calculators库用于计算不同类型及不同已知量的三角形面积
在triangle_area_calculators库中,有一个名为TriangleAreaCalculators的类
可以通过from triangle_area_calculators import TriangleAreaCalculators方式引用
import math
class TriangleAreaCalculators:
HALF = 0.5
@staticmethod
def area_by_base_height(base, height):
return TriangleAreaCalculators.HALF * base * height
@staticmethod
def area_by_heron(a, b, c):
p = (a + b + c) / 2
return math.sqrt(p * (p - a) * (p - b) * (p - c))
@staticmethod
def area_by_two_sides_angle(a, b, gamma_degrees):
gamma_radians = math.radians(gamma_degrees)
return TriangleAreaCalculators.HALF * a * b * math.sin(gamma_radians)
@staticmethod
def area_by_coordinates(x1, y1, x2, y2, x3, y3):
return TriangleAreaCalculators.HALF * abs(x1 * (y2 - y3) + x2 * (y3 - y1) + x3 * (y1 - y2))
@staticmethod
def area_by_vectors(A_x, A_y, B_x, B_y):
return TriangleAreaCalculators.HALF * abs(A_x * B_y - A_y * B_x)
@staticmethod
def area_of_right_triangle_by_two_legs(a, b):
return TriangleAreaCalculators.HALF * a * b
@staticmethod
def area_of_right_triangle_by_hypotenuse_and_leg(c, a):
theta_radians = math.acos(a / c)
return TriangleAreaCalculators.HALF * a * c * math.sin(theta_radians)
@staticmethod
def area_of_equilateral_triangle(a):
return (math.sqrt(3) / 4) * a ** 2
@staticmethod
def area_of_isosceles_triangle_by_base_angle(b, a, theta_degrees):
theta_radians = math.radians(theta_degrees)
return TriangleAreaCalculators.HALF * b * a * math.sin(theta_radians)
@staticmethod
def area_of_isosceles_triangle_by_height(b, h):
return TriangleAreaCalculators.HALF * b * h
@staticmethod
def area_of_isosceles_right_triangle(a):
return TriangleAreaCalculators.HALF * a ** 2
@staticmethod
def area_of_circumscribed_triangle(R, alpha_degrees):
alpha_radians = math.radians(alpha_degrees)
return TriangleAreaCalculators.HALF * R ** 2 * math.sin(alpha_radians)
'''
#使用示例
from triangle_area_calculators import TriangleAreaCalculators
# 示例1:使用底和高计算三角形面积
base = 5
height = 8
print("底为", base, "高为", height, "的三角形面积:", TriangleAreaCalculators.area_by_base_height(base, height))
# 示例2:使用海伦公式计算三角形面积(已知三边)
a = 3
b = 4
c = 5
print("三边分别为", a, b, c, "的三角形面积:", TriangleAreaCalculators.area_by_heron(a, b, c))
# 示例3:使用两边和夹角计算三角形面积(这里传入角度制角度)
a_side = 6
b_side = 8
angle_gamma_degrees = 60
print("两边分别为", a_side, b_side, "夹角为", angle_gamma_degrees, "度的三角形面积:", TriangleAreaCalculators.area_by_two_sides_angle(a_side, b_side, angle_gamma_degrees))
# 示例4:使用坐标法计算三角形面积
x1, y1 = 1, 1
x2, y2 = 3, 4
x3, y3 = 5, 2
print("坐标分别为(", x1, y1, "), (", x2, y2, "), (", x3, y3, ")的三角形面积:", TriangleAreaCalculators.area_by_coordinates(x1, y1, x2, y2, x3, y3))
# 示例5:使用向量法计算三角形面积
A_x, A_y = 2, 3
B_x, B_y = 5, 7
print("向量坐标分别为(", A_x, A_y, "), (", B_x, B_y, ")的三角形面积:", TriangleAreaCalculators.area_by_vectors(A_x, A_y, B_x, B_y))
# 示例6:计算直角三角形面积(已知两条直角边)
right_a = 3
right_b = 4
print("两条直角边分别为", right_a, b, "的直角三角形面积:", TriangleAreaCalculators.area_of_right_triangle_by_two_legs(right_a, right_b))
# 示例7:计算直角三角形面积(已知斜边和一条直角边)
right_c = 5
right_a = 3
print("斜边为", right_c, "一条直角边为", right_a, "的直角三角形面积:", TriangleAreaCalculators.area_of_right_triangle_by_hypotenuse_and_leg(right_c, right_a))
# 示例8:计算等边三角形面积
equilateral_a = 6
print("边长为", equilateral_a, "的等边三角形面积:", TriangleAreaCalculators.area_of_equilateral_triangle(equilateral_a))
# 示例9:计算等腰三角形面积(已知底边、等腰边和顶角,这里传入角度制角度)
isosceles_b = 4
isosceles_a = 5
isosceles_theta_degrees = 45
print("底边为", isosceles_b, "等腰边为", isosceles_a, "顶角为", isosceles_theta_degrees, "度的等腰三角形面积:", TriangleAreaCalculators.area_of_isosceles_triangle_by_base_angle(isosceles_b, isosceles_a, isosceles_theta_degrees))
# 示例10:计算等腰三角形面积(已知等腰边和底边上的高)
isosceles_a_side = 5
isosceles_height = 3
print("等腰边为", isosceles_a_side, "底边上的高为", isosceles_height, "的等腰三角形面积:", TriangleAreaCalculators.area_of_isosceles_triangle_by_height(isosceles_a_side, isosceles_height))
# 示例11:计算等腰直角三角形面积
isosceles_right_a = 4
print("边长为", isosceles_right_a, "的等腰直角三角形面积:", TriangleAreaCalculators.area_of_isosceles_right_triangle(isosceles_right_a))
# 示例12:计算圆内接三角形面积(这里传入角度制角度)
R_radius = 3
alpha_degrees = 90
print("圆半径为", R_radius, "中心角为", alpha_degrees, "度的圆内接三角形面积:", TriangleAreaCalculators.area_of_circumscribed_triangle(R_radius, alpha_degrees))
'''
代码链接🔗:
http://localhost:8888/tree
相关文章:

triangle_area_calculators库发布
最近将在pip网站上发布triangle_area_calculators库(我编写的python第三方库) triangle_area_calculators库用于计算不同类型及不同已知量的三角形面积 在triangle_area_calculators库中,有一个名为TriangleAreaCalculators的类 可以通过f…...

ClickHouse数据库SSL配置和SSL连接测试
目录 1.Server SSL配置介绍 2.Client SSL访问配置的介绍 3.my测试环境上开启ClickHouse Server SSL配置 & 客户端SSL访问的配置流程 4.附录 1)SSL证书的几种类型 单域名SSL证书 通配符SSL证书 多域名SSL证书 多域名通配符SSL证书 2)单域名…...

云渲染与汽车CGI图像技术优势和劣势
在数字时代,云渲染技术以其独特的优势在汽车CGI图像制作中占据了重要地位。云渲染通过利用云计算的分布式处理能力,将渲染任务分配给云端的服务器集群进行计算,从而实现高效、高质量的渲染效果。 这种技术的优势主要体现在以下几个方面&#…...
信号与噪声分析——第二节:随机变量的统计特征
2.1 单个随机变量的统计特征 随机变量是什么? 当随机变量X的取值个数是有限个的时候,我们称它为离散随机变量。 当随机变量X的取值个数是无限个的时候,我们称它为连续随机变量。 1. 分布函数和概率密度 1.分布函数 分布函数 定义为随机变…...

PHP网络爬虫常见的反爬策略
PHP网络爬虫在抓取数据时,常常会遭遇各种反爬策略。这些策略是网站为了保护自身数据不被恶意爬取而设置的。以下是一些常见的PHP网络爬虫反爬策略: IP限制: 这是最常见的反爬虫技术。通过限制IP的访问,可以有效防止恶意的爬虫攻击…...

java java.util.Scanner设置编码
在Java中,可以通过设置Scanner对象的编码来读取特定编码的输入。 使用Scanner的构造方法时,可以传入一个InputStream对象作为参数来设置编码。例如,如果要设置编码为UTF-8,可以这样写: InputStream inputStream Syst…...

小菜家教平台(二):基于SpringBoot+Vue打造一站式学习管理系统
目录 前言 今日进度 详细过程 一、数据库重构 二、编写登录接口 相关知识点 前言 昨天我们重启了小菜家教平台的开发,创建了新项目并初步进行了配置,今天我们继续。大家要是有需要源码的话可以在评论区跟我说,博客中就不添加源码了~ 今…...

Android AndroidManifest 文件内标签及属性
以下是重新排版后的文章: AndroidManifest 1. <manifest> 它是AndroidManifest.xml文件的根标签,包含了整个应用程序的基本信息,如应用程序的包名、版本代码、版本名称等。所有其他标签几乎都是在manifest标签内部定义的。 示例&…...

修改sql server 数据库的排序规则Chinese_PRC_CI_AS(字符集+排序)
文章目录 引言I 解决方案案例II 知识扩展排序规则SQL SERVER支持的所有排序规则引言 新增sql server 数据库实例的默认排序规则不支持中文存储,导致乱码 解决方案: 修改排序规则为Chinese_PRC_CI_AS 或者 Chinese_PRC_Stroke_CI_AS_WS或者Chinese_PRC_CI_AI_KS_WS 仅对新增…...

【ChatGPT】让ChatGPT在回答中附带参考文献与来源
让ChatGPT在回答中附带参考文献与来源 在撰写内容时,引用参考文献和来源可以增强信息的可信度和权威性。通过引导ChatGPT生成带有参考文献的回答,用户能够获取更可靠的信息和背景资料。本文将探讨如何有效地引导ChatGPT在回答中附带参考文献与来源。 一…...

云计算 在esxi 如何创建磁盘存储
重启启动...

大屏可视化:舞动数据与美观的“设计秘籍”
大屏可视化鉴赏:踏入软件系统产品设计之旅,让我们一同鉴赏那些闪耀在智慧农业、智慧园区、智慧社区及智慧港口等领域的大屏可视化杰作。每一帧画面,都是科技与创新的完美融合,数据跃然屏上,智慧触手可及。 >> 数…...
w~视觉~3D~合集1
我自己的原文哦~ https://blog.51cto.com/whaosoft/12316553 #SAFDNet 3D点云物体检测对自动驾驶感知至关重要,如何高效地从稀疏点云数据中学习特征表示是3D点云物体检测面临的一个关键挑战。我们在本文中将会介绍团队发表在NeurIPS 2023的HEDNet和CVPR 2024的SAFD…...

android 怎么查看依赖包的大小
Android 项目依赖包大小查看方案 在 Android 项目开发过程中,依赖包管理是一个非常重要的环节。了解每个依赖包的大小有助于我们优化应用性能,减少应用安装包的大小。本文将介绍一种方法来查看 Android 项目中各个依赖包的大小。 1. 环境准备 在开始之…...
HyperLogLog 的原理 详解
HyperLogLog(简称 HLL)是一种用于近似计数(特别是基数估计,Cardinality Estimation)的算法,它能够在大数据场景中高效地估计集合中不同元素的数量,尤其适用于数据流的情况。HyperLogLog 相较于传…...
OCR、语音识别与信息抽取:免费开源的AI平台在医疗领域的创新应用
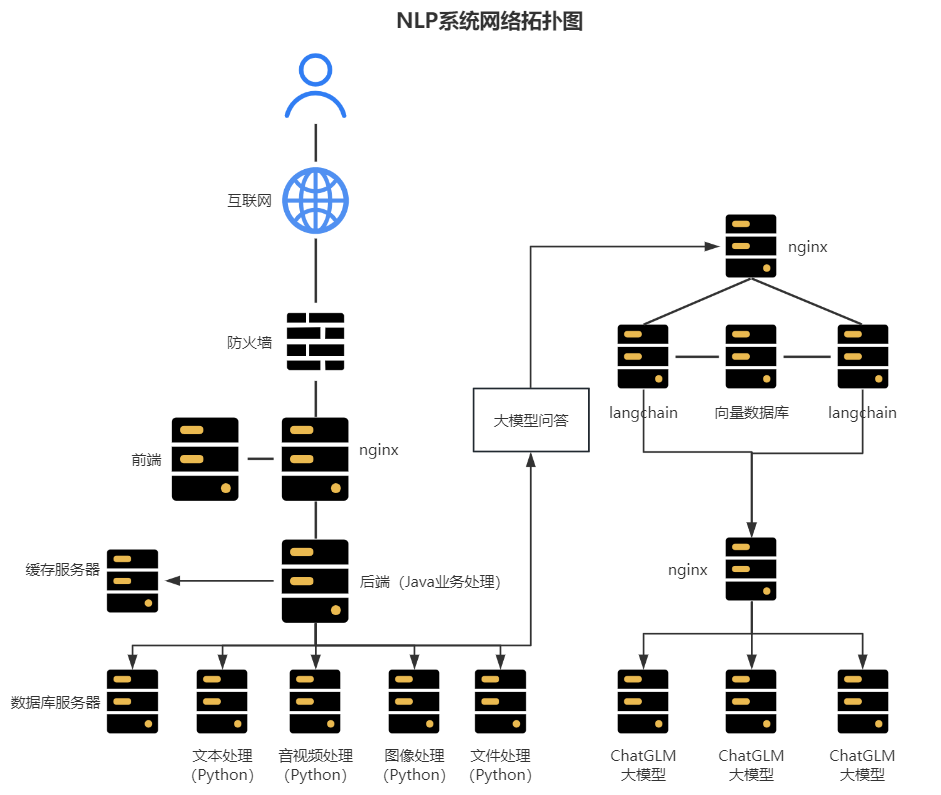
一、系统概述 在医疗行业中,大量数据来自手写病历、医学影像报告、患者对话记录等非结构化数据源。这些数据常常存在信息碎片化和管理困难的问题,给医务人员的工作带来了不便。思通数科AI多模态能力平台正是为了解决这一行业痛点而生,产品集…...

苍穹外卖Bug集合
初始化后端项目运行出现以下问题 以上报错是因为maven和jdk版本不符合,需要将jdk改成17,mavne改成3.9.9...

小菜家教平台(一):基于SpringBoot+Vue打造一站式学习管理系统
前言 现在已经学习了很多与Java相关的知识,但是迟迟没有进行一个完整的实践(之前这个项目开发到一半,很多东西没学搁置了,同时原先的项目中也有很多的问题),所以现在准备从零开始做一个基于SpringBootVue的…...

PyCharm中pylint安装与使用
目录 1. 安装插件2. pycharm中使用该功能3. 命令行使用 1. 安装插件 然后重启 2. pycharm中使用该功能 3. 命令行使用 前提是先 pip install pylint pylint demo01.py下面红框内容的意思是,得到10分/ 满分10分,上次运行获得8.33分,经调整…...

一篇文章了解TCP/IP模型
TCP/IP模型,即传输控制协议/互联网协议模型(Transmission Control Protocol/Internet Protocol Model),是互联网及许多其他网络上使用的分层通信模型。以下是对TCP/IP模型的详细介绍: 一、定义与组成TCP/IP模型是一个四…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...
