Java | Leetcode Java题解之第539题最小时间差
题目:

题解:
class Solution {public int findMinDifference(List<String> timePoints) {int n = timePoints.size();if (n > 1440) {return 0;}Collections.sort(timePoints);int ans = Integer.MAX_VALUE;int t0Minutes = getMinutes(timePoints.get(0));int preMinutes = t0Minutes;for (int i = 1; i < n; ++i) {int minutes = getMinutes(timePoints.get(i));ans = Math.min(ans, minutes - preMinutes); // 相邻时间的时间差preMinutes = minutes;}ans = Math.min(ans, t0Minutes + 1440 - preMinutes); // 首尾时间的时间差return ans;}public int getMinutes(String t) {return ((t.charAt(0) - '0') * 10 + (t.charAt(1) - '0')) * 60 + (t.charAt(3) - '0') * 10 + (t.charAt(4) - '0');}
}相关文章:

Java | Leetcode Java题解之第539题最小时间差
题目: 题解: class Solution {public int findMinDifference(List<String> timePoints) {int n timePoints.size();if (n > 1440) {return 0;}Collections.sort(timePoints);int ans Integer.MAX_VALUE;int t0Minutes getMinutes(timePoint…...

126页PPT麦肯锡战略实施与成本优化:质效提升与精益采购实践
麦肯锡企业PMO的各个阶段是一个结构化和系统化的过程,旨在确保项目的高效执行和成功交付。以下是麦肯锡企业PMO各个阶段的详细描述: 一、项目启动与规划阶段 此阶段的主要目标是明确项目目标、业务需求,以及制定项目章程和项目管理计划。 …...
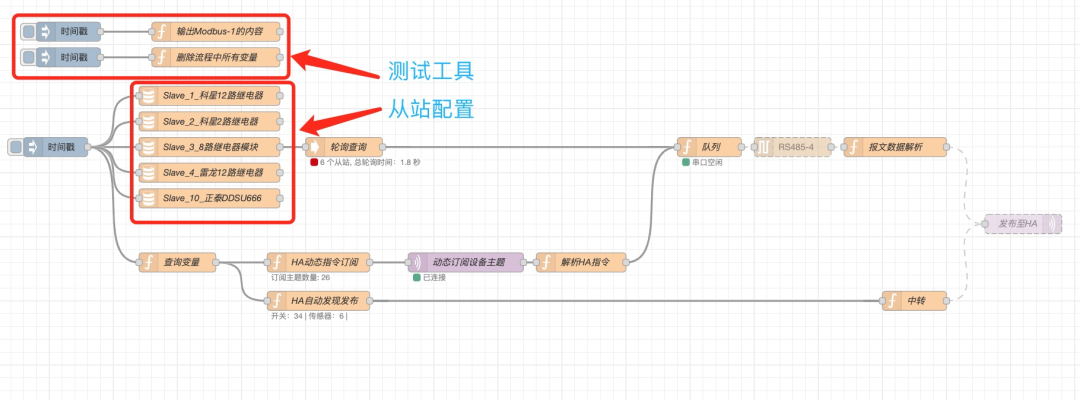
Modbus解析流程全面升级:体验全新核心与终极优化!
01 前言 本文章原文发表于我的微信公众号,请大家关注阅读,涉及的源代码等都在公众号,请搜索公众号: 智能家居NodeRed和HomeAssistant 即可关注。 02 全面改进的解析流程 前面发布过的Modbus解析流程在经过多个设备测试后发现存…...

【MWorks】Ubuntu 系统搭建
升级 Ubuntu系统 sudo apt-get update sudo apt-get upgrade安装流程 sudo chmod x 路径/文件.run安装 sudo 路径/文件.run安装过程中两个选项都填 y 打开安装对应的文件夹 运行 syslab.sh 文件,运行结束后,就可以在左上角开始搜索到syslab了。...

安装Element-Plus与v-model在vue3组件中的使用
安装Element-Plus 1.安装Element-Plus # 选择一个你喜欢的包管理器# NPM npm install element-plus --save# Yarn yarn add element-plus# pnpm pnpm install element-plus 2.main.ts中导入 import { createApp } from vue import { createPinia } from piniaimport App fr…...

Qt学习笔记第41到50讲
第41讲 UI美化遗留问题解决 如上图所示目前记事本的雏形已现,但是还是有待优化,比如右下角的拖动问题。 解决方法: ①首先修改了Widget类的构造函数。 Widget::Widget(QWidget *parent) : QWidget(parent) , ui(new Ui::Widget) {ui->s…...

加固筑牢安全防线:多源威胁检测响应在企业网络安全运营中的核心作用
随着网络攻防技术的演进,传统威胁检测技术手段已难以适应快速变化的威胁。多维度协同的攻击手段使得单一的检测技术难以应对复杂的网络安全威胁,企业需要更先进的检测技术来提升安全防护能力。 一、传统威胁检测技术与单一检测的局限性 传统威胁检测技术…...

用Python将PDF表格提取到文本、CSV和Excel文件中
从PDF文档中提取表格并将其转换为更易于处理的格式(如文本、CSV和Excel文件),是数据分析和信息管理中的常见需求。此过程可显著简化表格数据的处理,使数据的操作、分析和与其他数据集的集成更加便捷。无论是财务报表、研究论文&am…...

AIGC在游戏设计中的应用及影响
文章目录 一、AIGC的基本概念与背景AIGC的主要应用领域AIGC技术背景 二、AIGC在游戏设计中的应用1. 自动化游戏地图与关卡设计示例:自动生成2D平台游戏关卡 2. 角色与物品生成示例:使用GAN生成虚拟角色 3. 游戏剧情与任务文本生成示例:基于GP…...

给初学者的 Jupyter Notebook 教程
目录 一、什么是Jupyter Notebook? 1. 简介 2. 组成部分 ① 网页应用 ② 文档 3. Jupyter Notebook的主要特点 二、安装Jupyter Notebook 0. 先试用,再决定 1. 安装 ① 安装前提 ② 使用Anaconda安装 ③ 使用pip命令安装 三、运行Jupyter No…...

搜维尔科技:Xsens和BoB助力生物力学教育
Xsens和BoB助力生物力学教育 搜维尔科技:Xsens和BoB助力生物力学教育...

Vue动态计算Table表格的高度
因为每个用户不同的电脑屏幕宽高度,造成了Table表格的高度不一致,因此想要动态计算出table的高度,让其能够正常的铺满整个屏幕 代码 完整代码如下:首先计算 窗口的高度 - 搜索框的高度 - 固定数值 mounted () {// 计算搜索框的高…...

【MongoDB】MongoDB的聚合(Aggregate、Map Reduce)与管道(Pipline) 及索引详解(附详细案例)
文章目录 MongoDB的聚合操作(Aggregate)MongoDB的管道(Pipline操作)MongoDB的聚合(Map Reduce)MongoDB的索引 更多相关内容可查看 MongoDB的聚合操作(Aggregate) 简单理解ÿ…...

数组和字符串的es6新方法使用和综合案例
文章目录 一、数组1.forEach() 对数组中的每个元素执行回调函数,无返回值。2.map() 通过对数组中的每个元素执行回调函数生成新的数组3.filter() 过滤返回一个符合条件的新数组4.find() 返回符合条件的第一个数组元素,如果不存在则返回undefined5.every(…...

JS语法进阶第一课!—DOM(重点)
1、DOM概念 DOM 是 JavaScript 操作网页的接口,全称为“文档对象模型”(Document Object Model) 当网页被加载时,浏览器将网页转为一个DOM,并用JS进行各种操作。比如:改变页面中的HTML 元素及其属性&#x…...

Swift 开发教程系列 - 第5章:集合类型
Swift 提供了几种常用的集合类型,用于存储和管理一组数据。这些集合类型包括数组(Array)、字典(Dictionary)和集合(Set)。本章将介绍它们的使用方法及常见操作。 5.1 数组(Array&am…...

Spring:Bean(创建方式,抽象继承,工厂Bean,生命周期)
1,Bean的创建 1.1,调用构造器创建Bean 调用Bean类的无参构造函数来创造对象,因此要求提供无参构造函数。在这种情况下class元素是必须的,值就是Bean对象的实现类。 如果采用设值注入,Spring容器将使用默认的构造器来创…...

Flutter中的Extension关键字
目录 前言 一、什么是扩展(Extension) 二、扩展的语法 三、示例:为String 添加扩展方法 四、使用扩展的场景 五、复杂示例:为DateTime添加扩展 前言 在 Dart 和 Flutter 中,extension 关键字允许开发者为现有的类添加新的功能,而无需修改原有类的代…...

transformers 框架使用详解,bert-base-chinese
以 bert-base-chinese 模型为例,模型目录 model_name "C:/Users/Administrator.DESKTOP-TPJL4TC/.cache/modelscope/hub/tiansz/bert-base-chinese" bert-base-chinese 模型大小只有400多兆,参数的量级在百万级别,与现在动辄几十…...

STM32——ADC
目录 1、ADC的介绍 2、ADC主要特征 3、ADC结构与引脚 4、ADC配置流程 5、示例(光敏电阻的ADC采样) 6、提示 7、结语: 1、ADC的介绍 12位ADC是一种逐次逼近型模拟数字转换器。它有多达18个通道,可测量16个外部和2个内部 信号…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...
