基础算法——排序算法(冒泡排序,选择排序,堆排序,插入排序,希尔排序,归并排序,快速排序,计数排序,桶排序,基数排序,Java排序)
1.概述
比较排序算法
| 算法 | 最好 | 最坏 | 平均 | 空间 | 稳定 | 思想 | 注意事项 |
|---|---|---|---|---|---|---|---|
| 冒泡 | O(n) | O( n 2 n^2 n2) | O( n 2 n^2 n2) | O(1) | Y | 比较 | 最好情况需要额外判断 |
| 选择 | O( n 2 n^2 n2) | O( n 2 n^2 n2) | O( n 2 n^2 n2) | O(1) | N | 比较 | 交换次数一般少于冒泡 |
| 堆 | O( n l o g n nlogn nlogn) | O( n l o g n nlogn nlogn) | O( n l o g n nlogn nlogn) | O(1) | N | 选择 | 堆排序的辅助性较强,理解前先理解堆的数据结构 |
| 插入 | O(n) | O( n 2 n^2 n2) | O( n 2 n^2 n2) | O(1) | Y | 比较 | 插入排序对于近乎有序的数据处理速度比较快,复杂度有所下降,可以提前结束 |
| 希尔 | O(nlogn) | O( n 2 n^2 n2) | O( n l o g n nlogn nlogn) | O(1) | N | 插入 | gap序列的构造有多种方式,不同方式处理的数据复杂度可能不同 |
| 归并 | O( n l o g n nlogn nlogn) | O( n l o g n nlogn nlogn) | O( n l o g n nlogn nlogn) | O(n) | Y | 分治 | 需要额外的O(n)的存储空间 |
| 快速 | O( n l o g n nlogn nlogn) | O( n 2 n^2 n2) | O( n l o g n nlogn nlogn) | O(logn) | N | 分治 | 快排可能存在最坏情况,需要把枢轴值选取得尽量随机化来缓解最坏情况下的时间复杂度 |
非比较排序算法
| 非比较排序算法 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|
| 计数排序 | O(n+k) | O(n+k) | 稳定 |
| 桶排序 | O(n+k) | O(n+k) | 稳定 |
| 基数排序 | O(d*(n+k)) | O(n+k) | 稳定 |
其中
- n 是数组长度
- k 是桶长度
- d 是基数位数
稳定 vs 不稳定

说明:两个相同的数排序后没有发生改变,说明是稳定的
2.冒泡排序
- 每轮冒泡不断地比较相邻的两个元素,如果它们是逆序的,则交换它们的位置
- 下一轮冒泡,可以调整未排序的右边界,减少不必要比较
以数组 3、2、1 的冒泡排序为例,第一轮冒泡

第二轮冒泡

未排序区域内就剩一个元素,结束

public void bubbleSort(int[] nums) {for (int i = 0; i < nums.length - 1; i++) {for (int j = 0; j < nums.length - 1 - i; j++) {if (nums[j] > nums[j + 1]) {int temp = nums[j];nums[j] = nums[j + 1];nums[j + 1] = temp;}}}
}
优化手段:每次循环时,若能确定更合适的右边界,则可以减少冒泡轮数
以数组 3、2、1、4、5 为例,第一轮结束后记录的 x,即为右边界

public void bubbleSort(int[] nums) {int j = nums.length - 1;while (true) {int x = 0;for (int i = 0; i < j; i++) {if (nums[i] > nums[i + 1]) {int temp = nums[i];nums[i] = nums[i + 1];nums[i + 1] = temp;x = i;}}j = x;if (j == 0) {break;}}
}
3.选择排序
- 每一轮选择,找出最大(最小)的元素,并把它交换到合适的位置
以下面的数组选择最大值为例

public void selectSort(int[] nums) {for (int i = 0; i < nums.length - 1; i++) {for (int j = i + 1; j < nums.length; j++) {if (nums[i] > nums[j]) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}}}
}
4.堆排序
- 建立大顶堆
- 每次将堆顶元素(最大值)交换到末尾,调整堆顶元素,让它重新符合大顶堆特性
建堆

交换,下潜调整

public class HeapSort {public static void main(String[] args) {int[] nums = new int[]{3, 2, 1, 4, 5, 7, 9, 6, 8};new HeapSort().heapSort(nums);System.out.println(Arrays.toString(nums));}//堆排序public void heapSort(int[] nums) {//1.建堆操作,符合大顶堆的特性heapify(nums, nums.length);//2.每次将堆顶元素(最大值)交换到末尾,调整堆顶元素,让它重新符合大顶堆特性for (int i = nums.length - 1; i > 0; i--) {swap(nums, 0, i);down(nums, 0, i);//交换完了以后不符合大顶堆的特性}}//建堆private void heapify(int[] nums, int size) {//从倒数第一个非叶子节点开始以此下潜int start = (size - 2) / 2;//非叶子节点的索引for (int i = start; i >= 0; i--) {down(nums, i, size);}}//下潜private void down(int[] nums, int parent, int size) {/*** 方式一:递归实现*//*int left = 2 * parent + 1;int right = 2 * parent + 2;int max = parent;if (left < size && nums[left] > nums[max]) {max = left;}if (right < size && nums[right] > nums[max]) {max = right;}if (parent != max) {swap(nums, parent, max);down(nums, max, size);}*//*** 方式二:循环实现*/while (true) {int left = 2 * parent + 1;int right = 2 * parent + 2;int max = parent;if (left < size && nums[left] > nums[max]) {max = left;}if (right < size && nums[right] > nums[max]) {max = right;}if (parent == max) {break;}swap(nums, parent, max);parent = max;}}//交换private void swap(int[] nums, int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}
}
5.插入排序
- 将数组分为两部分 [0 … low-1] [low … a.length-1]
- 左边 [0 … low-1] 是已排序部分
- 右边 [low … a.length-1] 是未排序部分
- 每次从未排序区域取出 low 位置的元素, 插入到已排序区域

递归版
public void insertSort(int[] nums) {sort(nums, 1);
}private void sort(int[] nums, int low) {if (low == nums.length) {return;}int t = nums[low];int i = low - 1;while (i >= 0 && t < nums[i]) {nums[i + 1] = nums[i];i--;}if (i != low - 1) {nums[i + 1] = t;}sort(nums, low + 1);
}
非递归版
public void insertSort(int[] nums) {for (int low = 1; low < nums.length; low++) {int t = nums[low];int i = low - 1;while (i >= 0 && t < nums[i]) {nums[i + 1] = nums[i];i--;}if (i != low - 1) {nums[i + 1] = t;}}
}
6.希尔排序
- 简单的说,就是分组实现插入,每组元素间隙称为 gap
- 每轮排序后 gap 逐渐变小,直至 gap 为 1 完成排序
- 对插入排序的优化,让元素更快速地交换到最终位置
下图演示了 gap = 4,gap = 2,gap = 1 的三轮排序前后比较

public void shellSort(int[] nums) {for (int gap = nums.length >> 1; gap >= 1; gap = gap >> 1) {//原插入排序for (int low = gap; low < nums.length; low++) {int t = nums[low];int i = low - gap;while (i >= 0 && t < nums[i]) {nums[i + gap] = nums[i];i -= gap;}if (i != low - gap) {nums[i + gap] = t;}}}
}
7.归并排序
- 分 - 每次从中间切一刀,处理的数据少一半
- 治 - 当数据仅剩一个时可以认为有序
- 合 - 两个有序的结果,可以进行合并排序

递归实现
public class MergeSort {public static void main(String[] args) {int[] nums = new int[]{3, 2, 1, 4, 5, 7, 9, 6, 8, 0};new MergeSort().mergeSort(nums);System.out.println(Arrays.toString(nums));}private void mergeSort(int[] nums) {int[] merge = new int[nums.length];split(nums, merge, 0, nums.length - 1);}//对数组进行切分private void split(int[] nums, int[] merge, int left, int right) {if (left == right) {//不可再切了return;}//寻找中间点,以中间点进行切分int mid = (left + right) >>> 1;//切分split(nums, merge, left, mid);split(nums, merge, mid + 1, right);merge(nums, merge, left, mid, mid + 1, right);System.arraycopy(merge, left, nums, left, right - left + 1);}/*** 合并两个有序数组** @param array 原始数组* @param merge 合并后的数组* @param i 第一个有序范围的起始位置* @param iEnd 第一个有序范围的结束位置* @param j 第二个有序范围的起始位置* @param jEnd 第二个有序范围的结束位置*/private void merge(int[] array, int[] merge, int i, int iEnd, int j, int jEnd) {int k = i;while (i <= iEnd && j <= jEnd) {if (array[i] < array[j]) {merge[k] = array[i];i++;} else {merge[k] = array[j];j++;}k++;}if (i > iEnd) {System.arraycopy(array, j, merge, k, jEnd - j + 1);}if (j > jEnd) {System.arraycopy(array, i, merge, k, iEnd - i + 1);}}
}
非递归实现
public class MergeSort {public static void main(String[] args) {int[] nums = new int[]{3, 2, 1, 4, 5, 7, 9, 6, 8, 0};new MergeSort().mergeSort(nums);System.out.println(Arrays.toString(nums));}private void mergeSort(int[] nums) {int length = nums.length;int[] merge = new int[length];//width代表有序区间的宽度,取值是1,2,4,8for (int width = 1; width < length; width *= 2) {//[left,right]代表待合并区间的左右边界for (int left = 0; left < length; left += 2 * width) {int right = Integer.min(2 * width + left - 1, length - 1);int mid = Integer.min(left + width - 1, length - 1);merge(nums, merge, left, mid, mid + 1, right);}//合并数组System.arraycopy(merge, 0, nums, 0, length);}}/*** 合并两个有序数组** @param array 原始数组* @param merge 合并后的数组* @param i 第一个有序范围的起始位置* @param iEnd 第一个有序范围的结束位置* @param j 第二个有序范围的起始位置* @param jEnd 第二个有序范围的结束位置*/private void merge(int[] array, int[] merge, int i, int iEnd, int j, int jEnd) {int k = i;while (i <= iEnd && j <= jEnd) {if (array[i] < array[j]) {merge[k] = array[i];i++;} else {merge[k] = array[j];j++;}k++;}if (i > iEnd) {System.arraycopy(array, j, merge, k, jEnd - j + 1);}if (j > jEnd) {System.arraycopy(array, i, merge, k, iEnd - i + 1);}}
}
归并排序 + 插入排序
- 小数据量且有序度高时,插入排序效果高
- 大数据量用归并效果好
- 可以结合二者
public class MergeInsertSort {public static void main(String[] args) {int[] nums = new int[]{3, 2, 1, 4, 5, 7, 9, 6, 8, 0};new MergeInsertSort().mergeSort(nums);System.out.println(Arrays.toString(nums));}private void mergeSort(int[] nums) {int[] merge = new int[nums.length];split(nums, merge, 0, nums.length - 1);}private void split(int[] nums, int[] merge, int left, int right) {/*** 当元素数量少时,使用插入排序* 之前是切分至剩余一个元素时再合并*/if (right - left < 32) {insertSort(nums, left, right);return;}//寻找中间点,以中间点进行切分int mid = (left + right) >>> 1;//切分split(nums, merge, left, mid);split(nums, merge, mid + 1, right);merge(nums, merge, left, mid, mid + 1, right);System.arraycopy(merge, left, nums, left, right - left + 1);}public void insertSort(int[] nums, int left, int right) {for (int low = left + 1; low <= right; low++) {int t = nums[low];int i = low - 1;while (i >= left && t < nums[i]) {nums[i + 1] = nums[i];i--;}if (i != low - 1) {nums[i + 1] = t;}}}/*** 合并两个有序数组** @param array 原始数组* @param merge 合并后的数组* @param i 第一个有序范围的起始位置* @param iEnd 第一个有序范围的结束位置* @param j 第二个有序范围的起始位置* @param jEnd 第二个有序范围的结束位置*/private void merge(int[] array, int[] merge, int i, int iEnd, int j, int jEnd) {int k = i;while (i <= iEnd && j <= jEnd) {if (array[i] < array[j]) {merge[k] = array[i];i++;} else {merge[k] = array[j];j++;}k++;}if (i > iEnd) {System.arraycopy(array, j, merge, k, jEnd - j + 1);}if (j > jEnd) {System.arraycopy(array, i, merge, k, iEnd - i + 1);}}
}
8.快速排序
单边快排(lomuto分区)
- 选择最右侧元素作为基准点
- j 找比基准点小的,i 找比基准点大的,一旦找到,二者进行交换
- 交换时机:j 找到小的,且与 i 不相等
- i 找到 >= 基准点元素后,不应自增
- 最后基准点与 i 交换,i 即为基准点最终索引
例如:
i 和 j 都从左边出发向右查找,i 找到比基准点4大的5,j找到比基准点小的2,停下来交换

i 找到了比基准点大的5,j 找到比基准点小的3,停下来交换

j 到达right 处结束,right 与 i 交换,一轮分区结束

public class QuickSort {public static void main(String[] args) {int[] nums = new int[]{3, 2, 1, 4, 5, 7, 9, 6, 8, 0};new QuickSort().quickSort(nums);System.out.println(Arrays.toString(nums));}/*** 洛穆托分区方案** @param nums*/public void quickSort(int[] nums) {quick(nums, 0, nums.length - 1);}public void quick(int[] nums, int left, int right) {if (left >= right) {return;}int index = partition(nums, left, right);//返回基准点元素的索引quick(nums, left, index - 1);quick(nums, index + 1, right);}//分区操作,返回基准点元素的索引public int partition(int[] nums, int left, int right) {int value = nums[right];//基准点元素int i = left;int j = left;while (j < right) {if (nums[j] < value) {//找到比基准点小的值了if (i != j) {swap(nums, i, j);}i++;}j++;}swap(nums, i, right);return i;}public void swap(int[] nums, int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}
}
双边快排
- 选择最左侧元素作为基准点
- j 找比基准点小的,i 找比基准点大的,一旦找到,二者进行交换
- i 从左向右
- j 从右向左
- 最后基准点与 i 交换,i 即为基准点最终索引
例:
i 找到比基准点大的5停下来,j 找到比基准点小的1停下来(包含等于),二者交换

i 找到8,j 找到3,二者交换,i 找到7,j 找到2,二者交换

i == j,退出循环,基准点与 i 交换

public int partition(int[] nums, int left, int right) {int value = nums[left];//基准点元素int i = left;int j = right;while (i < j) {//j 从右向左找小的while (i < j && nums[j] > value) {j--;}//i 从左向右找大的while (i < j && nums[i] <= value) {i++;}//交换swap(nums, j, i);}swap(nums, left, i);return i;
}
优化
public int partition(int[] nums, int left, int right) {int index = ThreadLocalRandom.current().nextInt(right - left + 1) + left;swap(nums, index, left);int value = nums[left];//随机元素作为基准点元素int i = left;int j = right;while (i < j) {//j 从右向左找小的while (i < j && nums[j] > value) {j--;}//i 从左向右找大的while (i < j && nums[i] <= value) {i++;}//交换swap(nums, j, i);}swap(nums, left, i);return i;
}
解决数组中重复元素
public int partition(int[] nums, int left, int right) {int value = nums[left];//随机元素作为基准点元素int i = left + 1;int j = right;while (i <= j) {//j 从右向左找小的while (i <= j && nums[i] < value) {i++;}//i 从左向右找大的while (i <= j && nums[j] > value) {j--;}if (i <= j) {swap(nums, j, i);i++;j--;}}swap(nums, left, j);return j;
}
9.计数排序
- 确定范围:确定待排序数据中的最大值和最小值。
- 计数:创建一个计数数组,统计每个元素出现的次数。
- 累加计数:将计数数组转化为累加数组,确定每个元素在排序后的位置。
- 排序:将元素按照累加数组中的位置放入输出数组。
public void countSort(int[] nums) {//1.找出数组中的最大值与最小值int max = nums[0];int min = nums[0];for (int num : nums) {if (num > max) {max = num;}if (num < min) {min = num;}}//2.创建新数组,长度是 max - min + 1,用来保存原数组中的数据出现的次数int[] count = new int[max - min + 1];for (int num : nums) {count[num - min]++;}//3.循环新数组int k = 0;for (int i = 0; i < count.length; i++) {while (count[i] > 0) {nums[k++] = i + min;count[i]--;}}
}
10.桶排序
public void bucketSort(int[] nums) {//1.创建10个桶,每个桶里保存了一定的序列ArrayList<Integer>[] bucket = new ArrayList[10];//2.初始化for (int i = 0; i < bucket.length; i++) {bucket[i] = new ArrayList<>();}//3.把数据放入桶中for (int num : nums) {bucket[num / 10].add(num);}int k = 0;//4.排序每个桶内元素for (ArrayList<Integer> buck : bucket) {//转数组int[] array = buck.stream().mapToInt(i -> i).toArray();insertSort(array);//插入排序//遍历数组依次放入数组中for (int v : array) {nums[k++] = v;}}
}//插入排序
public void insertSort(int[] nums) {for (int low = 1; low < nums.length; low++) {int i = low - 1;int t = nums[low];while (i >= 0 && t < nums[i]) {nums[i + 1] = nums[i];i--;}if (i != low - 1) {nums[i + 1] = t;}}
}
通用
public void bucketSort(int[] nums, int range) {//1.找出数组中的最大值与最小值int max = nums[0];int min = nums[0];for (int num : nums) {if (num > max) {max = num;}if (num < min) {min = num;}}//1.创建10个桶,每个桶里保存了一定的序列ArrayList<Integer>[] bucket = new ArrayList[(max - min) / range + 1];//2.初始化for (int i = 0; i < bucket.length; i++) {bucket[i] = new ArrayList<>();}//3.把数据放入桶中for (int num : nums) {bucket[(num - min) / range].add(num);}int k = 0;//4.排序每个桶内元素for (ArrayList<Integer> buck : bucket) {//转数组int[] array = buck.stream().mapToInt(i -> i).toArray();insertSort(array);//插入排序//遍历数组依次放入数组中for (int v : array) {nums[k++] = v;}}
}
11.基数排序
基数排序(Radix Sort)是一种非比较型的排序算法,其基本原理是将整数按位数分配,然后按每个位数进行排序。基数排序的稳定性与子排序的稳定性有关。基数排序方法有几种,最常见的是LSD(Least Significant Digit,最低位优先)和MSD(Most Significant Digit,最高位优先)。
public class RadixSort {public static void main(String[] args) {String[] phoneNumbers = new String[]{"13812345678","13912345678","13612345678","13712345678","13512345678","13412345678","15012345678","15112345678","15212345678","15712345678"};new RadixSort().radixSort(phoneNumbers, 3);System.out.println(Arrays.toString(phoneNumbers));}public void radixSort(String[] nums, int length) {//1.准备10个桶并初始化ArrayList<String>[] buckets = new ArrayList[10];for (int i = 0; i < buckets.length; i++) {buckets[i] = new ArrayList<>();}//2.依次把数据放入桶内for (int i = length - 1; i >= 0; i--) {for (String num : nums) {buckets[num.charAt(i) - 48].add(num);}int k = 0;for (ArrayList<String> bucket : buckets) {for (String s : bucket) {nums[k++] = s;}bucket.clear();}}}
}
12.Java排序
Arrays.sort
JDK 7~13 中的排序实现
| 排序目标 | 条件 | 采用算法 |
|---|---|---|
| int[] long[] float[] double[] | size < 47 | 混合插入排序 (pair) |
| size < 286 | 双基准点快排 | |
| 有序度低 | 双基准点快排 | |
| 有序度高 | 归并排序 | |
| byte[] | size <= 29 | 插入排序 |
| size > 29 | 计数排序 | |
| char[] short[] | size < 47 | 插入排序 |
| size < 286 | 双基准点快排 | |
| 有序度低 | 双基准点快排 | |
| 有序度高 | 归并排序 | |
| size > 3200 | 计数排序 | |
| Object[] | -Djava.util.Arrays.useLegacyMergeSort=true | 传统归并排序 |
| TimSort |
JDK 14~20 中的排序实现
| 排序目标 | 条件 | 采用算法 |
|---|---|---|
| int[] long[] float[] double[] | size < 44 并位于最左侧 | 插入排序 |
| size < 65 并不是最左侧 | 混合插入排序 (pin) | |
| 有序度低 | 双基准点快排 | |
| 递归次数超过 384 | 堆排序 | |
| 对于整个数组或非最左侧 size > 4096,有序度高 | 归并排序 | |
| byte[] | size <= 64 | 插入排序 |
| size > 64 | 计数排序 | |
| char[] short[] | size < 44 | 插入排序 |
| 再大 | 双基准点快排 | |
| 递归次数超过 384 | 计数排序 | |
| size > 1750 | 计数排序 | |
| Object[] | -Djava.util.Arrays.useLegacyMergeSort=true | 传统归并排序 |
| TimSort |
- 其中 TimSort 是用归并+二分插入排序的混合排序算法
- 值得注意的是从 JDK 8 开始支持 Arrays.parallelSort 并行排序
- 根据最新的提交记录来看 JDK 21 可能会引入基数排序等优化
LeetCode题目
1题
912题

1122题
1636题
164题
相关文章:

基础算法——排序算法(冒泡排序,选择排序,堆排序,插入排序,希尔排序,归并排序,快速排序,计数排序,桶排序,基数排序,Java排序)
1.概述 比较排序算法 算法最好最坏平均空间稳定思想注意事项冒泡O(n)O( n 2 n^2 n2)O( n 2 n^2 n2)O(1)Y比较最好情况需要额外判断选择O( n 2 n^2 n2)O( n 2 n^2 n2)O( n 2 n^2 n2)O(1)N比较交换次数一般少于冒泡堆O( n l o g n nlogn nlogn)O( n l o g n nlogn nlogn)O( n l…...

几种常见的处理ARP欺骗的方法:静态ARP表和VLAN等
ARP(Address Resolution Protocol)欺骗是一种常见的网络攻击手段,攻击者通过伪造ARP响应,将网关的MAC地址指向攻击者的MAC地址,从而截获或篡改网络流量。为了应对ARP欺骗攻击,现代网络设备和管理员采取了一…...

突破1200°C高温性能极限!北京科技大学用机器学习合成24种耐火高熵合金,室温延展性极佳
在工程应用中,如燃气轮机、核反应堆和航空推进系统,对具备优异高温机械性能的金属合金需求十分旺盛。由于材料熔点的固有限制,传统镍基 (Ni) 高温合金的耐温能力已接近极限。为满足开发高温结构材料的需求,耐火高熵合金 (RHEAs) 于…...
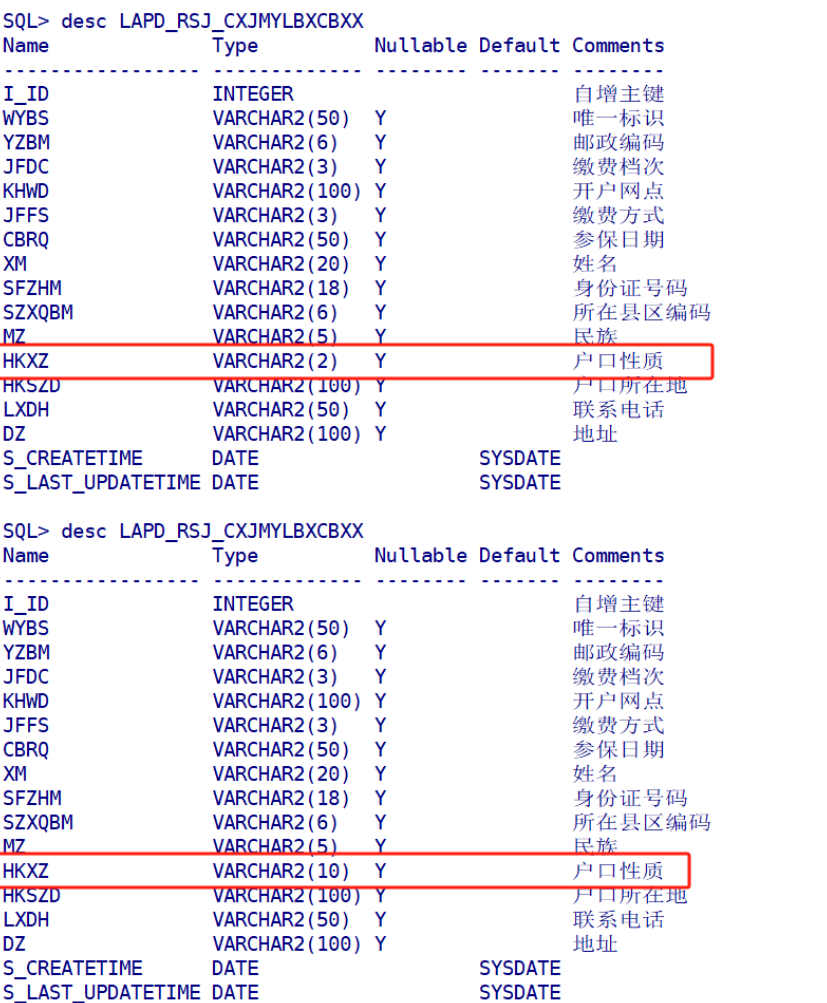
ORA-00054: 资源正忙, 但指定以 NOWAIT 方式获取资源 或者超时失效
数据治理过程中,有字段长度不够,扩展字段,报:ORA-00054: 资源正忙, 但指定以 NOWAIT 方式获取资源 或者超时失效 ALTER TABLE LAPD_RSJ_CXJMYLBXCBXX MODIFY HKXZ VARCHAR2(10);错误表示当前会话在试图访问的资源(通常…...

Python学习笔记-断点操作结合异常处理
在编程中,调试和错误处理是提升代码质量和开发效率的关键环节。调试能帮助识别并修复问题,异常处理则使得程序能在出现错误时有效地管理而不至于崩溃。断点与异常处理的结合应用是高级编程中不可或缺的技巧,能够帮助更高效地定位问题,提高程序的鲁棒性。 本文将通过详细的…...

Java实现JWT登录认证
文章目录 什么是JWT?为什么需要令牌?如何实现?添加依赖:JwtUtils.java(生成、解析Token的工具类)jwt配置:登录业务逻辑:其他关联代码:测试: 什么是JWT? JWT(Json Web Token&…...

「Mac畅玩鸿蒙与硬件20」鸿蒙UI组件篇10 - Canvas 组件自定义绘图
Canvas 组件在鸿蒙应用中用于绘制自定义图形,提供丰富的绘制功能和灵活的定制能力。通过 Canvas,可以创建矩形、圆形、路径、文本等基础图形,为鸿蒙应用增添个性化的视觉效果。本篇将介绍 Canvas 组件的基础操作,涵盖绘制矩形、圆…...

山东路远生态科技有限公司竣工投产仪式暨产品发布会圆满举行
第二十届三中全会于2024年7月15日至18日在北京举行。全会审议通过了《关于进一步全面深化改革、推进中国式现代化的决定》。其中提到,“要健全因地制宜发展新质生产力体制机制”。 新质生产力是由技术革命性突破、生产要素创新性配置、产业深度转型升级而催生的当代先进生产力…...

java: 题目:银行账户管理系统
题目:银行账户管理系统 设计一个简单的银行账户管理系统。要求实现以下功能: 1. 创建一个银行账户 BankAccount 类,该类具有以下属性:accountNumber(账户号码,类型为 String) balanceÿ…...

PH热榜 | 2024-11-06
DevNow 是一个精简的开源技术博客项目模版,支持 Vercel 一键部署,支持评论、搜索等功能,欢迎大家体验。 Github:https://github.com/LaughingZhu/DevNow 1. MindOne Builder 标语:这是一个“设计优先”的应用构建工具…...

五、Java并发 Java Google Guava 实现
Guava 是托管在 Github.com 上的流行的 Google 开源的 Java 线程池库。 Guava 包含了许多有用的并发类,同时还包含了几个方便的 ExecutorService 实现,但这些实现类都无法通过直接实例化或子类化来创建实例。取而代之的是提供了 MoreExecutors 助手类来…...
ssm公交车信息管理系统+vue
系统包含:源码论文 所用技术:SpringBootVueSSMMybatisMysql 免费提供给大家参考或者学习,获取源码看文章最下面 需要定制看文章最下面 目 录 摘要 I Abstract II 第1章 绪 论 1 1.1 研究背景 1 1.2 研究意义 1 1.3 国内外研究现状 …...

如何删除react项目的默认图标,使在浏览器中不显示默认图标favicon.ico
要删除 React 项目的默认图标,使在浏览器中不显示默认图标favicon.ico,其实有两种方法: 方法一 方法要点:删除掉 public 目录下的 favicon.ico 文件,再用浏览器访问时,如果加载不到图标文件,就…...

【React】react-app-env.d.ts 文件
在使用 create-react-app 生成的 TypeScript 项目模板中,react-app-env.d.ts 文件的作用是为 React 应用中的全局变量和类型进行声明。 全局类型声明:react-app-env.d.ts 文件会引入 react-scripts 提供的全局类型定义,这些类型定义扩展了 Ty…...
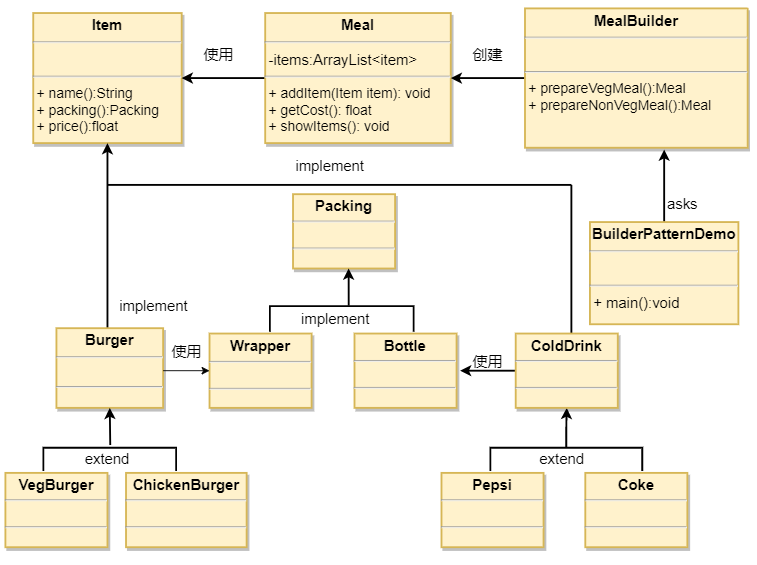
设计模式讲解01-建造者模式(Builder)
1. 概述 建造者模式也称为:生成器模式 定义:建造者模式是一种创建型设计模式,它允许你将创建复杂对象的步骤与表示方式相分离。 解释:建造者模式就是将复杂对象的创建过程拆分成多个简单对象的创建过程,并将这些简单…...

wflow-web:开源啦 ,高仿钉钉、飞书、企业微信的审批流程设计器,轻松打造属于你的工作流设计器
嗨,大家好,我是小华同学,关注我们获得“最新、最全、最优质”开源项目和高效工作学习方法 wflow-web是一个开源的工作流设计器,它支持可视化拖拽表单组件,动态任意层级结构审批节点,以及复杂流程条件的设置…...

Promise 简单介绍及深入挖掘
一、什么是 Promise? 在 JavaScript 中,Promise 是用于处理异步操作的一种方式。它代表了一个 可能 在将来某个时间点完成或失败的操作的结果。Promise 使得我们能够优雅地处理异步代码,避免了回调地狱(Callback Hell)…...

103 - Lecture 1
Introduction to Database 一、Introduction to Database Systems 1. 数据的定义 What is Data? EX: data could be a docx file storing your project status report; data could be a spreadsheet containing information • 数据只有在设计的场景中才有意义。ÿ…...

Ubuntu 20.04禁用或者移除 cloud-init
1、禁用cloud-init 这是最简单最安全的方法,在 /etc/cloud 目录下创建 cloud-init.disabled 文件重启后生效。删除该文件就可以恢复 # 创建cloud-init.disabled文件 sudo touch /etc/cloud/cloud-init.disabled # 重启 reboot 2、移除 cloud-init 软件包及文件夹…...

DevOps开发运维简述
DevOps平台是一套集成的解决方案,旨在协调软件开发(Development)和信息技术运维(Operations)。它促进跨功能团队合作,实现自动化流程,确保持续集成与持续交付(CI/CD)。 一…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...
