归并排序:高效算法的深度解析
一、归并排序概述
归并排序是一种基于分治思想的经典排序算法。它的核心操作分为三个主要步骤:分割、排序和合并。
首先是分割步骤,将待排序的数组不断地分成更小的子数组,直到每个子数组中只有一个元素。例如,对于一个包含多个元素的数组,不断地进行对半分割,直到每个子部分都只有一个元素为止。
接着是排序步骤,由于单个元素的子数组本身就是有序的,所以在这个阶段实际上并没有真正的排序操作。
最后是合并步骤,将两个已排序的子数组合并成一个更大的有序数组。在合并过程中,通过比较两个子数组的元素,将较小的元素依次放入新的数组中,直到两个子数组中的所有元素都被处理完毕。这个过程不断重复,最终将所有的子数组合并成一个完全有序的数组。
归并排序的时间复杂度为 ,其中 是待排序数组的长度。这是因为每次分割操作将问题规模减半,而合并操作的时间复杂度与问题规模呈线性关系。归并排序的稳定性使得它在某些特定的应用场景中具有优势,特别是当需要保持相等元素的相对顺序时。总的来说,归并排序以其高效和稳定的特性,在计算机科学的各种领域中都有广泛的应用。
二、归并排序的核心步骤
(一)分割过程
- 递归实现分割:按照深度优先方式,先拆左边再拆右边,设定递归终止条件。在归并排序中,递归实现分割是一种常见的方法。首先,找到数组的中间位置,将数组分为左右两部分。然后,对左右两部分分别进行递归调用,继续分割,直到每个子数组中只有一个元素为止。这个过程可以看作是深度优先的方式,先深入到最左边的子数组进行分割,然后再逐步返回并处理右边的子数组。递归的终止条件是当子数组的长度为 1 或 0 时,因为单个元素的子数组本身就是有序的。
例如,对于一个长度为 8 的数组,首先找到中间位置,分为左右两个长度为 4 的子数组。然后对这两个子数组继续进行分割,直到每个子数组的长度为 1。在这个过程中,递归的深度为 。
- 非递归实现分割:借助栈机制,考虑细节进行深度优先的拆分过程。非递归实现分割可以借助栈的数据结构来模拟递归的过程。首先,将整个数组的范围压入栈中。然后,从栈中弹出一个范围,进行分割,并将分割后的两个子范围压入栈中。重复这个过程,直到栈为空。在这个过程中,需要考虑一些细节问题,比如如何确定子数组的范围、如何处理边界情况等。
例如,假设我们有一个长度为 8 的数组,初始时将范围 [0, 7] 压入栈中。弹出这个范围后,将其分为 [0, 3] 和 [4, 7],并将这两个子范围压入栈中。接着,继续弹出栈顶的范围进行分割,直到每个子数组的长度为 1。
(二)合并过程
- 比较两个子数组元素,较小元素放入新数组,对应指针前进。在合并过程中,首先比较两个已排序的子数组的首元素。将较小的元素放入一个新的数组中,并将对应子数组的指针向前移动一位。然后继续比较两个子数组的下一个元素,重复这个过程,直到其中一个子数组的所有元素都被处理完毕。
例如,假设有两个子数组 A=[2, 4, 6] 和 B=[1, 3, 5]。首先比较 A [0] 和 B [0],因为 1<2,所以将 1 放入新数组中,并将 B 的指针向前移动一位。接着比较 A [0] 和 B [1],因为 2<3,所以将 2 放入新数组中,并将 A 的指针向前移动一位。
- 处理剩余元素,直接放入新数组,因每一组内元素有序。当一个子数组的所有元素都被处理完毕后,另一个子数组中可能还有剩余的元素。由于每个子数组本身是有序的,所以可以直接将剩余的元素依次放入新数组中。
例如,在上一步的例子中,当比较完 A [2] 和 B [2] 后,B 子数组中的元素已经全部处理完毕,而 A 子数组中还有元素 4 和 6。这时,可以直接将 4 和 6 依次放入新数组中。
三、归并排序的代码实现
(一)多种语言示例
- C 语言代码实现:
在 C 语言中实现归并排序通常需要以下几个关键步骤。首先是申请空间,就像这样:
| #define N 7 void merge(int arr[], int low, int mid, int high){ int i, k; int *tmp = (int *)malloc((high-low+1)*sizeof(int)); |
接着在合并过程中,比较两个子数组的元素,将较小的元素放入临时数组tmp中:
| for(k=0; left_low<=left_high && right_low<=right_high; k++){ if(arr[left_low]<=arr[right_low]){ tmp[k] = arr[left_low++]; }else{ tmp[k] = arr[right_low++]; } } |
最后,如果一个子数组还有剩余元素,直接复制到临时数组中,并将临时数组的元素复制回原数组:
| if(left_low <= left_high){ for(i=left_low;i<=left_high;i++) tmp[k++] = arr[i]; } if(right_low <= right_high){ for(i=right_low; i<=right_high; i++) tmp[k++] = arr[i]; } for(i=0; i<high-low+1; i++) arr[low+i] = tmp[i]; free(tmp); return; |
- C++ 代码实现:
- 递归实现:
C++ 的归并排序可以通过递归的方式实现。先找到中间位置,将数组分成两部分,分别进行递归排序,然后再合并。
| void mergeSort(int A[],int p,int r){ if(p<r){ int q=(p+r)/2; mergeSort(A,p,q); mergeSort(A,q+1,r); merge(A,p,q,r); } return; } |
- 循环实现:
也可以通过循环的方式实现归并排序。循环中每次将数组分成大小为size的子数组,然后进行合并。当size大于等于数组长度时,排序完成。
| void mergeSortIterative(vector<int>& arr) { int n = arr.size(); for (int size = 1; size < n; size *= 2) { for (int left = 0; left < n - size; left += 2 * size) { int mid = left + size - 1; int right = min(left + 2 * size - 1, n - 1); merge(arr, left, mid, right); } } } |
这种方式展示了一些精妙的代码优化成果,通过循环逐步合并子数组,减少了递归带来的开销。
- Java 代码实现:
- 手写归并排序:
在 Java 中,手写归并排序需要明确功能、寻找递推关系、确定终止条件。首先确定分界点,将待排序数组分成左右两部分,然后递归处理左右数组部分。最后将排序好的左右两部分数组合并成新数组,并确保合并后的数组依然有序。
| public static int[] temp; public static void merge_sort(int[] q, int l, int r) { if (l >= r) { return; } int mid = (l + r) / 2; merge_sort(q, l, mid); merge_sort(q, mid + 1, r); int k = 0, i = l, j = mid + 1; temp = new int[r - l + 1]; while (i <= mid && j <= r) { if (q[i] <= q[j]) { temp[k++] = q[i++]; } else { temp[k++] = q[j++]; } } while (i <= mid) { temp[k++] = q[i++]; } while (j <= r) { temp[k++] = q[j++]; } for (i = l, j = 0; i <= r; i++, j++) { q[i] = temp[j]; } } |
- 分析性能:
归并排序在 Java 中的时间复杂度为 ,其中 是待排序数组的长度。空间复杂度为 ,因为需要一个临时数组来存储排序过程中的数据。归并排序是稳定的排序算法,这意味着相等元素的相对顺序在排序后不会改变。
- Python 代码实现:
- 多路归并排序:
在 Python 中,可以实现多路归并排序。多路归并排序通常借助优先队列或自己实现小顶堆来处理大规模数据集。首先,将每个数据块分别排序,然后将这些有序的数据块进行多路归并。
| def merge(lst1, lst2): lst3 = [] i1, i2 = 0, 0 n1, n2 = len(lst1), len(lst2) while i1 < n1 and i2 < n2: if lst1[i1] < lst2[i2]: lst3.append(lst1[i1]) i1 = i1 + 1 else: lst3.append(lst2[i2]) i2 = i2 + 1 if i1 == n1: for i in lst2[i2:]: lst3.append(i) else: for i in lst1[i1:]: lst3.append(i) return lst3 def mergeSort(nums): n = len(nums) if n <= 1: return nums m = n // 2 left = mergeSort(nums[:m]) right = mergeSort(nums[m:]) return merge(left, right) |
- 处理大规模数据集:
对于大规模数据集,多路归并排序可以有效地利用内存和处理器资源,提高排序效率。通过将数据集分成多个较小的数据块,分别进行排序,然后再进行合并,可以减少内存占用和排序时间。
- PHP 代码实现:
- 展示合并和拆分过程的具体代码:
在 PHP 中,归并排序可以通过递归和非递归两种方式实现。以下是递归方式的实现代码:
| function mergeSort(&$arr, $left, $right) { if ($left < $right) { $mid = floor(($left + $right) / 2); mergeSort($arr, $left, $mid); mergeSort($arr, $mid + 1, $right); merge($arr, $left, $mid, $right); } } function merge(&$arr, $left, $mid, $right) { $i = $left; $j = $mid + 1; $temp = array(); while ($i <= $mid && $j <= $right) { if ($arr[$i] < $arr[$j]) { $temp[] = $arr[$i]; $i++; } else { $temp[] = $arr[$j]; $j++; } } while ($i <= $mid) { $temp[] = $arr[$i]; $i++; } while ($j <= $right) { $temp[] = $arr[$j]; $j++; } for($k = 0; $k < count($temp); $k++) { $arr[$left + $k] = $temp[$k]; } } |
非递归方式的实现代码如下:
| function mSort(&$arr) { $len = count($arr); $size = 1; while ($size <= $len - 1) { $left = 0; while ($left + $size <= $len - 1) { $mid = $left + $size - 1; $right = $mid + $size; if ($right > $len - 1) { $right = $len - 1; } merge($arr, $left, $mid, $right); $left = $right + 1; } $size *= 2; } } function merge(&$arr, $left, $mid, $right) { $i = $left; $j = $mid + 1; $temp = array(); while ($i <= $mid && $j <= $right) { if ($arr[$i] < $arr[$j]) { $temp[] = $arr[$i]; $i++; } else { $temp[] = $arr[$j]; $j++; } } while ($i <= $mid) { $temp[] = $arr[$i]; $i++; } while ($j <= $right) { $temp[] = $arr[$j]; $j++; } for ($i = $left, $k = 0; $i <= $right; $i++, $k++) { $arr[$i] = $temp[$k]; } } |
这些代码展示了归并排序在 PHP 中的具体实现,帮助理解归并排序的整体流程。
(二)代码性能分析
- 时间复杂度:
- 无论在最坏、最佳还是平均情况下,归并排序的时间复杂度均为 。这是因为每次分割操作将问题规模减半,而合并操作的时间复杂度与问题规模呈线性关系。例如,对于一个长度为 的数组,分割操作需要进行 次,每次分割后的合并操作需要 的时间复杂度,所以总的时间复杂度为 。
- 空间复杂度:
- 归并排序在排序过程中需要使用辅助数组,空间复杂度为 。这是因为在合并过程中,需要一个临时数组来存储合并后的结果。例如,对于一个长度为 的数组,在合并过程中需要一个长度为 的临时数组来存储合并后的结果。
- 稳定性:
- 归并排序是一种稳定排序。这意味着在排序过程中,相等元素的相对顺序不会改变。例如,对于一个包含多个相等元素的数组,归并排序会保持这些相等元素的相对顺序不变。
- 是否原地排序:
- 归并排序不是原地排序,因为它需要使用辅助数组来存储合并后的结果。原地排序是指在排序过程中不需要额外的存储空间,只需要在原数组上进行操作。例如,冒泡排序、插入排序和选择排序都是原地排序算法。
四、归并排序的应用场景
归并排序在处理大规模数据集方面具有显著优势,尤其适用于小内存排序大文件等情况。
例如,在面对外存中有 100G 的字符串文件,而只有 1G 内存的情况下,归并排序可以发挥重要作用。首先将 100G 的内容分成若干个小部分,每个部分不超过 500MB。分别读取这些小部分进行排序,然后写入到外存中,这样就得到了若干个已经排好序的小部分。接着进行多路归并排序,对于多个已经排好序的小部分,每次取出它们各自的最小值,找到最小值中的最小值,写入到外存,同时将最小值所在外存区域指针向右移动。每次比较最小值需要比较 k-1 次,总共有 n-1 轮,所以时间复杂度为 O ((n-1)*(k-1))。这里还可以使用胜者树(完全二叉树)优化找最小值的过程,对第一次的查找建立一颗胜者树,找到最小值后,读取最小值所在外存区域的新值,然后修改胜者树对应节点的值,沿着从该结点到根结点的路径修改这棵二叉树,最多操作 log (k) 次。这样总体排序的时间复杂度就可以降为 O (nlogk)。
此外,使用 Python 实现多 (K) 路归并外部排序,可以解决小内存排序大文件问题。绕不开归并核心思想,分治,先拆成小文件,再排序,最后合并所有碎片文件成一个大文件。首先,大文件拆分成多个 block_size 大的小文件,每个小文件排好序。然后,将拆分成的小文件合并起来,然后将归并的东西写到大文件里面去,这里用到的是多路归并的方法。
在实际工作中,多个有序数列合并成一个,大文件或多个大文件合并成一个并排序的需求常见并不少见。比如现在有四路数据:a0:[1, 3, 6, 7],a1: [],a2: [3, 5, 7, 19],a3: [9, 12, 87, 98]。可以使用多路归并排序的方法,先保存每路最小值,用 min_map 保存每一路的当前最小值,然后获取最小值中的最小值,将其取出并检查被取出值的那一路是否还剩下其他元素,如果存在,则修改 min_map 里面对应的值,如果不存在,则删除掉 min_map 里面对应的记录,以表示该路已经没有元素需要遍历了。最终将多个有序数组合并起来。
总的来说,归并排序以其高效的处理大规模数据集的能力,在实际应用中具有广泛的应用场景。
相关文章:

归并排序:高效算法的深度解析
一、归并排序概述 归并排序是一种基于分治思想的经典排序算法。它的核心操作分为三个主要步骤:分割、排序和合并。 首先是分割步骤,将待排序的数组不断地分成更小的子数组,直到每个子数组中只有一个元素。例如,对于一个包含多个…...
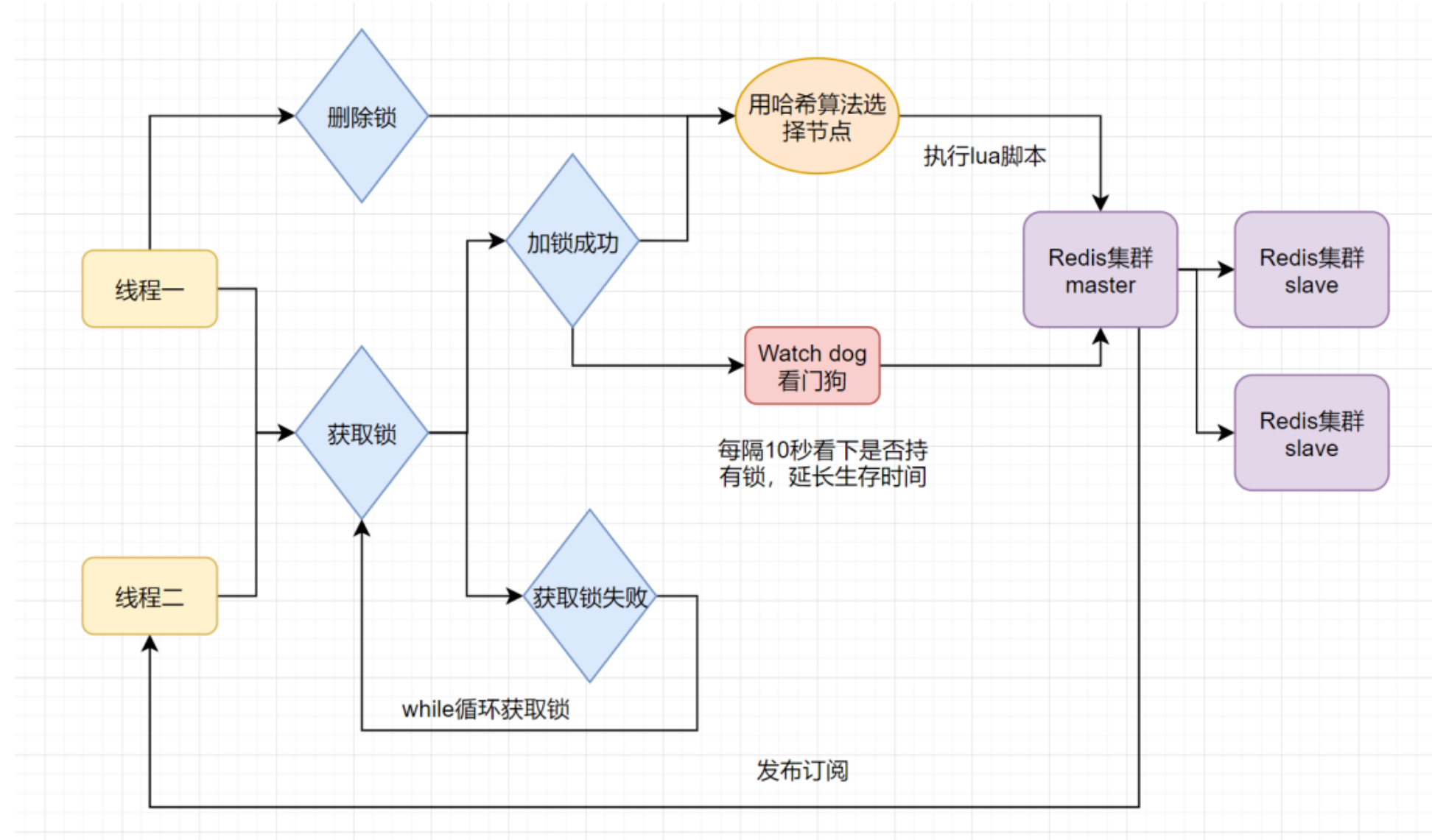
微服务中常用分布式锁原理及执行流程
1.什么是分布式锁 分布式锁是一种在分布式系统环境下实现的锁机制,它主要用于解决,多个分布式节点之间对共享资源的互斥访问问题,确保在分布式系统中,即使存在有多个不同节点上的进程或线程,同一时刻也只有一个节点可…...

声学气膜馆助力企业年会与研学活动完美呈现—轻空间
在现代企业和教育活动中,场地的选择往往决定了活动的成败。尤其是在企业年会、研学基地等重要场合,选择一个既能满足多功能需求又能快速搭建的场地至关重要。而声学气膜馆正是为这种需求量身打造的理想场所。凭借其独特的声学性能和灵活的结构设计&#…...

Halcon3D image_points_to_world_plane详解
分三个部分来聊聊这个算子 一,算子的参数介绍 二,算法的计算过程 三,举例实现 第一部分,算子的介绍 image_points_to_world_plane( : : CameraParam, WorldPose, Rows, Cols, Scale : X, Y) 参数介绍: CameraParam,:相机内参 WorldPose 世界坐标系,也叫物体坐标系(成…...

A Consistent Dual-MRC Framework for Emotion-cause Pair Extraction——论文阅读笔记
前言 这是我第一次向同学院同年级的学生和老师们汇报的第一篇论文,于2022年发表在TOIS上,属于CCF A类,主要内容是将MRC应用到情感原因对抽取中。 论文链接:用于情绪-原因对提取的一致双 MRC 框架 |信息系统上的 ACM Transactions 这里我就不放上我自己翻译的中文版还有我…...

如何debug(Eclipse)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 2分钟教会你如何Java中DeBug【IDEA中Java】 在eclipse中如何使用Debug进行调试 双击左侧打断点(取消断点同样双击) 右上角进入debug界面(常用) 选择所需断点位置(勾选右侧需要测试的断点位置) 启动…...
【comfyui教程】ComfyUI有趣工作流推荐:快速换脸,创意随手掌握!
前言 在数字影像处理和创意表达领域,ComfyUI 绝对是你的得力助手!今天我们推荐一个非常有趣的工作流——快速换脸。无论你是图像编辑小白,还是深耕AI影像的达人,这个工作流都能让你快速实现面部迁移,体验全新的照片玩…...

css-flex布局属性
flex 布局的优势 flex 布局的子元素不会脱离文档流flex 是一种现代的布局方式,是 W3C 第一次提供真正用于布局的 CSS 规范 弹性盒子、子元素 弹性盒子:指的是使用 display:flex 或 display:inline-flex 声明的父容器 声明:使用 display:fl…...

【鸿蒙】HarmonyOS NEXT应用开发快速入门教程之布局篇(下)
系列文章目录 【鸿蒙】HarmonyOS NEXT开发快速入门教程之ArkTS语法装饰器(上) 【鸿蒙】HarmonyOS NEXT开发快速入门教程之ArkTS语法装饰器(下) 【鸿蒙】HarmonyOS NEXT应用开发快速入门教程之布局篇(上) 【…...

高阶函数--python
高阶函数应当满足至少下面一个条件: 接受一个或多个函数参数 输出一个函数 下面用一个例子来理解高阶函数。 一、高阶函数 先看一个简单的函数 例一: 例二: 是高阶函数,因为满足条件,返回一个函数 并且有闭包&a…...

MYSQL备库的并行复制
备库在消费中转日志时,其实可以分多个线程同时对多个事务进行消费,但是要满足2个基本原则: 1.涉及同一行数据的多个事务必须在同一个线程中执行,否则会导致数据不一致 2.同一个事务不能被拆开 MYSQL 5.6的并行复制策略ÿ…...

体感游戏开发:参考资料
体感游戏开发是一个涉及多个领域知识和技能的过程,以下是一些参考资料和建议,以帮助开发者更好地进行体感游戏开发: 一、技术文档和指南 游戏开发引擎文档 Unity、Unreal Engine等主流游戏开发引擎提供了详细的文档和教程,涵盖从…...

Diving into the STM32 HAL-----Clock Tree笔记
几乎每个数字电路都需要一种方法来同步其内部电路或与其他电路同步。时钟是一种产生周期性信号的设备,它是数字电子学中最普遍的心跳源形式。 然而,相同的时钟信号不能用于馈送现代微控制器(如 STM32 微控制器)提供的所有组件和外…...

【AIGC】如何充分利用ChatGPT:有效提示框架与基本规则
概述 在使用ChatGPT进行内容创作时,遵循结构化的提示框架和基本规则可以显著提升AI响应的质量。本文探讨了五种结构化的提示框架,并详细介绍了基本规则和进阶技巧,帮助您更有效地与ChatGPT互动。 基础规则 规则1:指令放在开头&…...

【1个月速成Java】基于Android平台开发个人记账app学习日记——第7天,申请阿里云SMS短信服务SDK
系列专栏链接如下,方便跟进: https://blog.csdn.net/weixin_62588253/category_12821860.html?fromshareblogcolumn&sharetypeblogcolumn&sharerId12821860&sharereferPC&sharesourceweixin_62588253&sharefromfrom_link 同时篇幅…...

视频怎么去除杂音保留人声?教你如何实现视频降噪
在视频录制的过程中,可能会产生很多杂音和噪音,这可能时因为录制环境不理想、录制设备故障等多方面造成的。视频怎么去除杂音保留人声?今天我们就来谈谈如何实现视频降噪。 视频中常见的杂音类型 自然环境音:如风声、水流声、鸟叫…...
:使用Python基于Fuzzy WSM、Fuzzy WPM、Fuzzy WASPAS的多准则决策分析)
数学建模学习(136):使用Python基于Fuzzy WSM、Fuzzy WPM、Fuzzy WASPAS的多准则决策分析
1. 算法介绍 1.1 Fuzzy WSM、Fuzzy WPM、Fuzzy WASPAS 的基本概念和背景 模糊多属性决策(MADM)方法是解决复杂决策问题的重要工具,尤其是在信息不确定且难以量化的情况下。Fuzzy WSM(Fuzzy Weighted Sum Model)、Fuzzy WPM(Fuzzy Weighted Product Model)、以及 Fuzzy…...

Python小游戏21——拼图小游戏
使用了Pygame库来创建图形界面。请确保你已经安装了Pygame库(可以使用pip install pygame来安装)。 运行结果展示 代码展示 python import pygame import sys import random # 初始化Pygame pygame.init() # 设置屏幕尺寸 screen_width, screen_height …...

C# 常用的测试框架合集
在 C# 开发中,拥有强大的测试框架是确保代码质量和稳定性的关键。本文将介绍一些 C# 中常用的测试框架,帮助你更好地进行单元测试、集成测试等各类测试工作。 一、NUnit 简介 NUnit 是一个广泛使用的开源测试框架,专为.NET 平台设计。它提供…...

Android——从相机/相册获取图片
从相机获取图片 设置权限 <uses-permission android:name"android.permission.CAMERA" />点击跳转 private static final int REQUEST_CODE_TAKE 1;public void takePhoto(View view) {if (ContextCompat.checkSelfPermission(this, Manifest.permission.CAM…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...
