前端vue3若依框架pnpm run dev启动报错
今天前端vue3若依框架pnpm run dev启动报错信息:

> ruoyi@3.8.8 dev D:\AYunShe\2024-11-6【无锡出门证】\wuxi-exit-permit-web
> vite
error when starting dev server:
Error: listen EACCES: permission denied 0.0.0.0:80
at Server.setupListenHandle [as _listen2] (node:net:1723:21)
at listenInCluster (node:net:1788:12)
at Server.listen (node:net:1876:7)
at httpServer.listen (file:///D:/AYunShe/2024-11-6%E3%80%90%E6%97%A0%E9%94%A1%E5%87%BA%E9%97%A8%E8%AF%81%E3%80%91/wuxi-exit-permit-web/node_modules/.pnpm/vite@5.3.2_@types+node@22.9.0_sass@1.77.5/node_modules/vite/dist/node/chunks/dep-C1-ZB6nQ.js:63438:14)
ELIFECYCLE Command failed with exit code 1.
原因:
由于端口80通常需要管理员权限才能使用,你可以尝试更换一个不需要管理员权限的端口。例如,
pnpm run dev -- --host 0.0.0.0 --port 3000来启动开发服务器,将端口改为3000。
或者:在vite.config.js文件里把端口改成8000
重新启动就不报错了。

相关文章:

前端vue3若依框架pnpm run dev启动报错
今天前端vue3若依框架pnpm run dev启动报错信息: > ruoyi3.8.8 dev D:\AYunShe\2024-11-6【无锡出门证】\wuxi-exit-permit-web > vite error when starting dev server: Error: listen EACCES: permission denied 0.0.0.0:80 at Server.setupListenHand…...

python线条爱心
效果图 代码 import math from turtle import * def hearta(k):return 15*math.sin(k)**3 def heartb(k):return 12*math.cos(k)-5*\math.cos(2*k)-2*\math.cos(3*k)-\math.cos(4*k) speed(1000) bgcolor("black") for i in range(6000):goto(hearta(i)*20,heartb(…...

GPU的内存是什么?
GPU(图形处理器)的内存是指专门用于 GPU 存储数据的内存,也被称为显存。 一、显存的作用: 1、存储图像数据 当计算机要显示图像时,显存会存储屏幕上每个像素点的颜色、亮度等信息。例如,对于一个分辨率为 1…...
)
Linux - 弯路系列1:xshell能够连接上linux,但xftp连不上(子账号可以连接,但不能上传数据)
问题如题目阐述。 注:所有操作在root账户下操作。 解决办法: 1、确认连接设置 服务器地址和端口:确保在 Xftp 中输入的服务器地址和端口号与 Xshell 使用的相同。默认情况下,SFTP 使用端口 22。 用户凭证:检查用户名…...

数组逆序重存放
题目描述 将一个数组中的值按逆序重新存放。例如,原来的顺序为8,6,5,4,1。要求改为1,4,5,6,8。 输入 输入为两行:第一行数组中元素的个数n(1<n<100),第二行是n个整数,每两个整数之间用空格分隔。 输出 输出…...

归并排序:高效算法的深度解析
一、归并排序概述 归并排序是一种基于分治思想的经典排序算法。它的核心操作分为三个主要步骤:分割、排序和合并。 首先是分割步骤,将待排序的数组不断地分成更小的子数组,直到每个子数组中只有一个元素。例如,对于一个包含多个…...
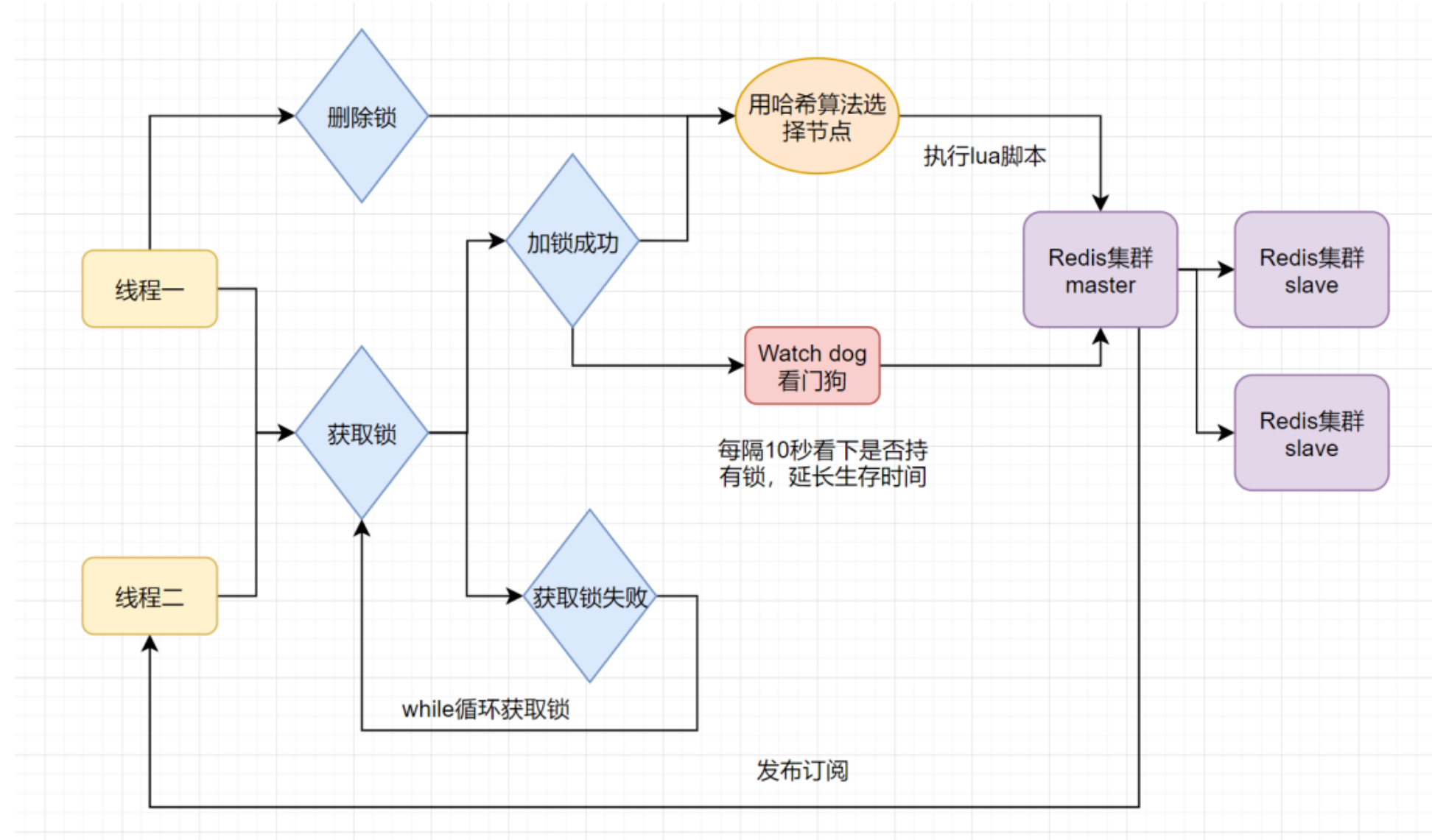
微服务中常用分布式锁原理及执行流程
1.什么是分布式锁 分布式锁是一种在分布式系统环境下实现的锁机制,它主要用于解决,多个分布式节点之间对共享资源的互斥访问问题,确保在分布式系统中,即使存在有多个不同节点上的进程或线程,同一时刻也只有一个节点可…...

声学气膜馆助力企业年会与研学活动完美呈现—轻空间
在现代企业和教育活动中,场地的选择往往决定了活动的成败。尤其是在企业年会、研学基地等重要场合,选择一个既能满足多功能需求又能快速搭建的场地至关重要。而声学气膜馆正是为这种需求量身打造的理想场所。凭借其独特的声学性能和灵活的结构设计&#…...

Halcon3D image_points_to_world_plane详解
分三个部分来聊聊这个算子 一,算子的参数介绍 二,算法的计算过程 三,举例实现 第一部分,算子的介绍 image_points_to_world_plane( : : CameraParam, WorldPose, Rows, Cols, Scale : X, Y) 参数介绍: CameraParam,:相机内参 WorldPose 世界坐标系,也叫物体坐标系(成…...

A Consistent Dual-MRC Framework for Emotion-cause Pair Extraction——论文阅读笔记
前言 这是我第一次向同学院同年级的学生和老师们汇报的第一篇论文,于2022年发表在TOIS上,属于CCF A类,主要内容是将MRC应用到情感原因对抽取中。 论文链接:用于情绪-原因对提取的一致双 MRC 框架 |信息系统上的 ACM Transactions 这里我就不放上我自己翻译的中文版还有我…...

如何debug(Eclipse)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 2分钟教会你如何Java中DeBug【IDEA中Java】 在eclipse中如何使用Debug进行调试 双击左侧打断点(取消断点同样双击) 右上角进入debug界面(常用) 选择所需断点位置(勾选右侧需要测试的断点位置) 启动…...
【comfyui教程】ComfyUI有趣工作流推荐:快速换脸,创意随手掌握!
前言 在数字影像处理和创意表达领域,ComfyUI 绝对是你的得力助手!今天我们推荐一个非常有趣的工作流——快速换脸。无论你是图像编辑小白,还是深耕AI影像的达人,这个工作流都能让你快速实现面部迁移,体验全新的照片玩…...

css-flex布局属性
flex 布局的优势 flex 布局的子元素不会脱离文档流flex 是一种现代的布局方式,是 W3C 第一次提供真正用于布局的 CSS 规范 弹性盒子、子元素 弹性盒子:指的是使用 display:flex 或 display:inline-flex 声明的父容器 声明:使用 display:fl…...

【鸿蒙】HarmonyOS NEXT应用开发快速入门教程之布局篇(下)
系列文章目录 【鸿蒙】HarmonyOS NEXT开发快速入门教程之ArkTS语法装饰器(上) 【鸿蒙】HarmonyOS NEXT开发快速入门教程之ArkTS语法装饰器(下) 【鸿蒙】HarmonyOS NEXT应用开发快速入门教程之布局篇(上) 【…...

高阶函数--python
高阶函数应当满足至少下面一个条件: 接受一个或多个函数参数 输出一个函数 下面用一个例子来理解高阶函数。 一、高阶函数 先看一个简单的函数 例一: 例二: 是高阶函数,因为满足条件,返回一个函数 并且有闭包&a…...

MYSQL备库的并行复制
备库在消费中转日志时,其实可以分多个线程同时对多个事务进行消费,但是要满足2个基本原则: 1.涉及同一行数据的多个事务必须在同一个线程中执行,否则会导致数据不一致 2.同一个事务不能被拆开 MYSQL 5.6的并行复制策略ÿ…...

体感游戏开发:参考资料
体感游戏开发是一个涉及多个领域知识和技能的过程,以下是一些参考资料和建议,以帮助开发者更好地进行体感游戏开发: 一、技术文档和指南 游戏开发引擎文档 Unity、Unreal Engine等主流游戏开发引擎提供了详细的文档和教程,涵盖从…...

Diving into the STM32 HAL-----Clock Tree笔记
几乎每个数字电路都需要一种方法来同步其内部电路或与其他电路同步。时钟是一种产生周期性信号的设备,它是数字电子学中最普遍的心跳源形式。 然而,相同的时钟信号不能用于馈送现代微控制器(如 STM32 微控制器)提供的所有组件和外…...

【AIGC】如何充分利用ChatGPT:有效提示框架与基本规则
概述 在使用ChatGPT进行内容创作时,遵循结构化的提示框架和基本规则可以显著提升AI响应的质量。本文探讨了五种结构化的提示框架,并详细介绍了基本规则和进阶技巧,帮助您更有效地与ChatGPT互动。 基础规则 规则1:指令放在开头&…...

【1个月速成Java】基于Android平台开发个人记账app学习日记——第7天,申请阿里云SMS短信服务SDK
系列专栏链接如下,方便跟进: https://blog.csdn.net/weixin_62588253/category_12821860.html?fromshareblogcolumn&sharetypeblogcolumn&sharerId12821860&sharereferPC&sharesourceweixin_62588253&sharefromfrom_link 同时篇幅…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
