MySQL —— Innodb 索引数据结构
文章目录
- 不用平衡二叉树或红黑树作为索引
- B树适合作为索引
- 比B树更适合作为索引的结构——B+树
- 总结
MySQL 使用 B+树索引数据结构(因为默认使用 innodb 存储引擎)
- B树:有序数组 + 平衡多叉树;
- B+树:有序数组链表 + 平衡多叉树;
不用平衡二叉树或红黑树作为索引
普通二叉树:
- 二叉树的查找的时间复杂度是 O ( l o g 2 N ) O(log_2N) O(log2N),其查找效率与深度有关,而普通的二叉树可能由于内部节点排列问题退化成链表。例如,按顺序插入一组递增的数值,可能导致树变成一条链表,在这种情况下,树的深度变为 N,查找的时间复杂度退化为 O ( N ) O(N) O(N),这与链表的查找效率相同。这样查找效率就会很低。
1\2\3\4
平衡二叉树
- 平衡二叉树是更好的选择,通过自平衡机制保持平衡,即通过旋转调整结构保持最小的深度,所有节点的左右子树高度差不能超过 1,确保了查找、插入和删除操作的时间复杂度保持在 O ( l o g 2 N ) O(log_2N) O(log2N)。
为什么平衡二叉树不适合作为索引呢?
-
索引通常存储在磁盘上的索引文件中。在数据表很大的情况下,索引也会很大,因此无法一次性将全部索引加载到内存当中。数据库系统通常以页(如 4KB、8KB 或 16KB)为单位从磁盘中读取一个磁盘页的数据量到内存中,为了找到指定索引的磁盘页,可能会导致多次磁盘 I/O 操作才能完成。而这个磁盘的读取的速度较内存中的读取速度而言是差了好几个级别,磁盘的随机访问时间可能是内存访问时间的数百倍至数千倍,这意味着每次从磁盘读取数据时,都会消耗较多的时间。
- 每个节点只有两个子节点,这导致树的高度可能较大。当树的深度增加时,查找时需要的磁盘 I/O 操作也会相应增加。例如,在最坏情况下,查找可能需要访问树的每一层,而每一层都需要从磁盘读取数据。
- 每个节点只有两个子节点,这导致树的高度可能较大。当树的深度增加时,查找时需要的磁盘 I/O 操作也会相应增加。例如,在最坏情况下,查找可能需要访问树的每一层,而每一层都需要从磁盘读取数据。
-
平衡二叉树在逻辑结构上相近的节点在树的结构中是相邻的,其物理实现是使用数组来存储节点。虽然在逻辑上相邻的节点可能在物理数组中相距较远,因此,每次读取的磁盘页的数据中有许多是用不上的。因此,查找过程中要进行许多次的磁盘读取操作。
-
平衡二叉树各节点之间在逻辑上存在一定的关系,但在物理实现却是随机的,比如父子关系或兄弟关系的两个节点子逻辑上相邻之类的,但在物理实现上却是分散的。对于使用磁盘预读(局部性原理),每次从磁盘读取一页,读取的是物理结构上连续的一段数据,这样就会读取许多无用的信息(接下来很大机会不会用到);
-
其次就是二叉树每个节点只能存储一个关键字及其相关信息,不能充分利用磁盘预读功能;
-
-
而适合作为索引的结构应该是尽可能少的执行磁盘IO操作,因为执行磁盘IO操作非常的耗时。因此,平衡二叉树并不适合作为索引结构。
总结:
- 使用红黑树(平衡二叉树)结构的话,每次磁盘预读中的很多数据是用不上的数据。因此,它没能利用好磁盘预读的提供的数据。
- 然后又由于深度大(较B树而言),所以进行的磁盘IO操作更多。
B树适合作为索引
平衡二叉树没能充分利用磁盘预读功能,而B树是为了充分利用磁盘预读功能来而创建的一种数据结构,也就是说B树就是为了作为索引才被发明出来的的。
- B 树的设计旨在最大限度地减少磁盘访问次数,特别是在处理大量数据时。由于磁盘访问速度远低于内存访问速度,减少 I/O 操作对于提高整体性能至关重要;
- B 树结构允许每个节点包含多个关键字和子节点,这意味着在一次磁盘读取中可以获取更多的数据。这样,B树能够高效地利用磁盘的读取特性,特别是在顺序访问时;
B树的结构特点
- 多叉结构:与平衡二叉树不同,B 树的每个节点可以有多个子节点,这使得树的高度显著降低,从而减少了查找和更新时所需的 I/O 操作;
- 节点内存储多个关键字:B 树的每个节点可以存储多个关键字,这样在每次读取磁盘页时,可以同时获取多个数据项,充分利用了磁盘的预读能力;
局部性原理与磁盘预读:
-
由于存储介质的特性,磁盘的存取速度远低于内存,传统机械硬盘的访问时间受机械运动的影响,磁盘的存取速度往往是主存的几百分分之一,这使得磁盘 I/O 成为性能瓶颈,尤其是在需要频繁读取数据时。因此为了提高效率,要尽量减少磁盘 I/O。为了达到这个目的,磁盘读取往往不是严格按需读取,而是每次都会预读,读取一段连续的数据(称为一页),即使只需要一个字节,磁盘也会从这个位置开始,顺序向后读取一定长度的数据放入内存。这样做的目的是利用磁盘的顺序读取特性,提高读取效率。这样做的理论依据是计算机科学中著名的局部性原理;
-
局部性原理:局部性原理是指在程序运行过程中,访问的数据往往集中在某些特定区域。当一个数据项被访问时,其附近的数据项很可能也会被访问。这种现象在许多程序中普遍存在。由于磁盘顺序读取的效率很高(不需要寻道时间,只需很少的旋转时间),因此对于具有局部性的程序来说,预读可以提高I/O效率;
在操作系统中,磁盘 I/O 的读取和写入通常以页(page)为单位进行。页是固定大小的数据块,一页的数据量有多大跟操作系统有关,常见的大小有 4KB、8KB 或 16KB。也就是我们读取一页内的数据时候,实际上才发生了一次IO,这个理论对于索引的数据结构设计非常有帮助;
-
磁盘预读是具体实现,其理论依据是局部性原理。
B树适合作为索引
B 树的每个节点可以存储多个关键字,它将节点大小设置为磁盘页的大小,充分利用了磁盘预读的功能。每次读取磁盘页时就会读取一整个节点。也正因每个节点存储着非常多个关键字,树的深度就会非常的小。进而要执行的磁盘读取操作次数就会非常少,更多的是在内存中对读取进来的数据进行查找。
- 每个节点可以存储多个关键字,可以充分利用了磁盘预读的功能;
- B 树的深度会非常的小,减小磁盘 I/O 操作。
B树的查询,主要发生在内存中,而平衡二叉树的查询,则是发生在磁盘读取中。因此,虽然B树查询查询的次数不比平衡二叉树的次数少,但是相比起磁盘IO速度,内存中比较的耗时就可以忽略不计了。因此,B树更适合作为索引。
比B树更适合作为索引的结构——B+树
B+树中的B不是代表二叉(binary),而是代表平衡(balance),因为B+树是从最早的平衡二叉树演化而来,但是 B+树不是一个二叉树。
MySQL 中也是使用B+树作为索引。它是B树的变种,因此是基于B树来改进的。
B+树的关键字全部存放在叶子节点中,非叶子节点用来做索引,而叶子节点中有一个指针指向一下个叶子节点。做这个优化的目的是为了提高区间访问(遍历)的性能。
-
B树必须用中序遍历的方法按序扫库,而B+树直接从叶子结点挨个扫一遍就完了,B+树支持 range-query 非常方便,而B树不支持。这是数据库选用B+树的最主要原因。
比如说:
我们要查找关键字范围在3到7的关键字,在找到第一个符合条件的数字3后,访问完第一个关键字所在的块后,得遍历这个B树,获取下一个块,直到遇到一个不符合条件的关键字。遍历的过程是比较复杂的。(即B树遍历完一块后,需要查询B树得到下一块,然后再遍历)相比之下,B+树的基于范围的查询简洁很多。由于叶子节点有指向下一个叶子节点的指针,因此从块1到块2的访问,通过块1指向块2的指针即可,从块2到块3也是通过一个指针即可。(B+树遍历完一块后,可以通过指针指向下一块继续遍历) -
B+树只要遍历叶子节点就可以实现整棵树的遍历。而且在数据库中基于范围的查询是非常频繁的,而B树不支持这样的操作(或者说效率太低)。
b+树的查找过程:
-
如图所示,如果要查找数据项29,那么首先会把磁盘块1由磁盘加载到内存,此时发生一次IO,在内存中用二分查找确定29在17和35之间,锁定磁盘块1的P2指针,内存时间因为非常短(相比磁盘的IO)可以忽略不计,通过磁盘块1的P2指针的磁盘地址把磁盘块3由磁盘加载到内存,发生第二次IO,29在26和30之间,锁定磁盘块3的P2指针,通过指针加载磁盘块8到内存,发生第三次IO,同时内存中做二分查找找到29,结束查询,总计三次IO。真实的情况是,3层的b+树可以表示上百万的数据,如果上百万的数据查找只需要三次IO,性能提高将是巨大的,如果没有索引,每个数据项都要发生一次IO,那么总共需要百万次的IO,显然成本非常非常高。

一颗b+树,浅蓝色的块我们称之为一个磁盘块,可以看到每个磁盘块包含几个数据项(深蓝色所示)和指针(黄色所示),如磁盘块1包含数据项17和35,包含指针P1、P2、P3,P1表示小于17的磁盘块,P2表示在17和35之间的磁盘块,P3表示大于35的磁盘块。真实的数据存在于叶子节点即3、5、9、10、13、15、28、29、36、60、75、79、90、99。非叶子节点不存储真实的数据,只存储指引搜索方向的数据项,如17、35并不真实存在于数据表中。
总结:用B+树的主要原因是B树在提高了磁盘IO性能的同时并没有解决元素遍历的效率低下的问题。正是为了解决这个问题,B+树应运而生。
总结
B树:
-
B树就是一个节点可以拥有多于2个子节点的多叉查找树。
-
叶子节点和非叶子节点都储存关键字和真实数据项,每个节点不仅用于索引,还包含实际的数据。因为非叶子节点要保存数据项,所以一个节点(块)能保存的索引少,相对于B+树访问磁盘IO时就多; -
B树是有序数组+平衡多叉树;
B+树:
-
B+树是基于B树来改进的。
-
非叶子节点只存储关键字,用于索引搜索路径,而不存储实际的数据项,所有真实数据只存储在叶子节点中。因为非叶子节点不保存数据项,所以一个节点(块)能保存的索引多,相对于B树访问磁盘IO时就少,尽管在内存遍历的次数变多,但内存访问比磁盘快很多,相对于访问磁盘,访问内存的时间几乎可以不计。 -
B+树:有序数组链表+平衡多叉树;
树的所有叶子节点构成一个有序链表,可以按照主键排序的次序遍历全部记录。B+Tree 所有真实数据都在叶子节点上,并且增加了顺序访问指针,每个叶子节点都有指向相邻叶子节点的指针,便于区间查找和遍历。
B树与B+树对比:
B树结构在所有的节点里存储索引信息和数据项;B+树结构没有在所有的节点里存储记录数据项,而是只在最下层的叶子节点存储,上层的所有非叶子节点只存放索引信息。- B树是有序数组+平衡多叉树;B+树是有序数组链表+平衡多叉树。B+树使用双向链表串连所有叶子节点,区间查询效率更高,因为所有数据都在B+树的叶子节点,但是B树则需要通过中序遍历才能完成查询范围的查找。
- B+树每次都必须查询到叶子节点才能找到数据,而B树查询的数据可能不在叶子节点,也可能在,这样就会造成查询的效率的不稳定。
- B+树查询效率更高,因为B+树矮更胖,高度小,查询产生的I/O最少。因为非叶子节点不保存数据项,所以一个节点(块)能保存的关键字(索引)更多,所以一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。
B+ 树的优点在于:
- IO次数更少(相对于其他数据结构):由于B+树在内部节点上不包含数据信息,因此在内存页中能够存放更多的key。 数据存放的更加紧密,具有更好的空间局部性。因此访问叶子节点上关联的数据也具有更好的缓存命中率。
- 数据库系统的设计者巧妙利用了磁盘预读原理,将一个节点的大小设为等于一个页,这样每个节点需要一次I/O就可以完全载入。
- 遍历更加方便(相对于B树结构):B+树的叶子结点都是相链的,因此对整棵树的遍历只需要一次线性遍历叶子结点即可。而且由于数据顺序排列并且相连,所以便于区间查找和搜索。而B树则需要进行每一层的递归遍历。相邻的元素可能在内存中不相邻,所以缓存命中性没有B+树好。
- 这样做是为了提高区间效率,例如查询key为从18到49的所有数据记录,当找到18后,只要顺着节点和指针顺序遍历就可以以此向访问到所有数据节点,极大提高了区间查询效率。
B树优点:
- 但是B树也有优点,其优点在于,由于B树的每一个节点都包含key和value,因此经常访问的元素可能离根节点更近,因此访问也更迅速。下面是B 树和B+树的区别图:

为什么MySQL选择B+树做索引
1、 B+树的磁盘读写代价更低:B+树的内部节点并没有指向关键字具体信息的指针,因此其内部节点相对B树更小,如果把所有同一内部节点的关键字存放在同一盘块中,那么盘块所能容纳的关键字数量也越多,一次性读入内存的需要查找的关键字也就越多,相对IO读写次数就降低了。
2、B+树的查询效率更加稳定:由于非终结点并不是最终指向文件内容的结点,而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同,导致每一个数据的查询效率相当。
3、B+树更便于遍历:由于B+树的数据都存储在叶子结点中,分支结点均为索引,方便扫库,只需要扫一遍叶子结点即可,但是B树因为其分支结点同样存储着数据,我们要找到具体的数据,需要进行一次中序遍历按序来扫,所以B+树更加适合在区间查询的情况,所以通常B+树用于数据库索引。
4、B+树更适合基于范围的查询:B树在提高了IO性能的同时并没有解决元素遍历的我效率低下的问题,正是为了解决这个问题,B+树应用而生。B+树只需要去遍历叶子节点就可以实现整棵树的遍历。而且在数据库中基于范围的查询是非常频繁的,而B树不支持这样的操作或者说效率太低。
参考1
参考2
相关文章:

MySQL —— Innodb 索引数据结构
文章目录 不用平衡二叉树或红黑树作为索引B树适合作为索引比B树更适合作为索引的结构——B树总结 MySQL 使用 B树索引数据结构(因为默认使用 innodb 存储引擎) B树:有序数组 平衡多叉树;B树:有序数组链表 平衡多叉树…...

探索C语言数据类型
目录 前言 一、基本数据类型 1.整型(Integer) 2.浮点型(Floating - point) 3.字符型(Character) 4.布尔型(Boolean) 二、派生数据类型 1.数组(Array)…...

凌晨官宣离婚,他们为何让老粉直呼天塌?
你说的是影视飓风MediaStorm的创始人Tim和小鱼吧,他们确实在11月5日凌晨官宣离婚了。以下是具体介绍:官宣离婚2024年11月5日凌晨,影视飓风MediaStorm的创始人Tim(潘天鸿)在社交媒体上发文,宣布与小鱼&#…...

Spring Boot 导出 Excel 文件
本文将详细介绍如何使用 Spring Boot 和 Apache POI 实现 Excel 文件的导出功能,帮助开发者快速上手。 1. 准备工作 首先,确保你的 Spring Boot 项目已成功创建并运行。接下来,需要在 pom.xml 文件中添加 Apache POI 相关依赖,以…...

HTTPSOK:SSL/TLS证书自动续期工具
HTTPSOK 是一个支持 SSL/TLS 证书自动续期 的工具,旨在简化 SSL 证书的管理,尤其是自动化处理证书续期的工作。对于大多数网站而言,SSL 证书的续期是一项必要但容易被忽视的工作,因为 SSL 证书的有效期通常为 90 天。使用 HTTPSOK…...
Uniapp安装Pinia并持久化(Vue3)
安装pinia 在uni-app的Vue3版本中,Pinia已被内置,无需额外安装即可直接使用(Vue2版本则内置了Vuex)。 HBuilder X项目:直接使用,无需安装。CLI项目:需手动安装,执行yarn add pinia…...

基于Dpabi和spm12的脑脊液(csf)分割和提取笔记
一、前言 脑脊液(csf)一直被认为与新陈代谢有重要关联,其为许多神经科学研究提供重要价值,从fMRI图像中提取脑脊液信号可用于多种神经系统疾病的诊断。特别是自2019年Science上那篇著名的csf-BOLD文章发表后,大家都试图…...

【每日一题】2012考研数据结构 - 求字符串链表公共后缀
本篇文章将为大家讲解一道关于链表的经典题目——求两个链表的共同后缀节点。该问题在实际开发中同样具有很大的应用价值,是每一位数据结构学习者不可错过的重要题目。 问题描述 假设我们有一个带头结点的单链表来保存单词,每个节点包含一个字符和指向…...
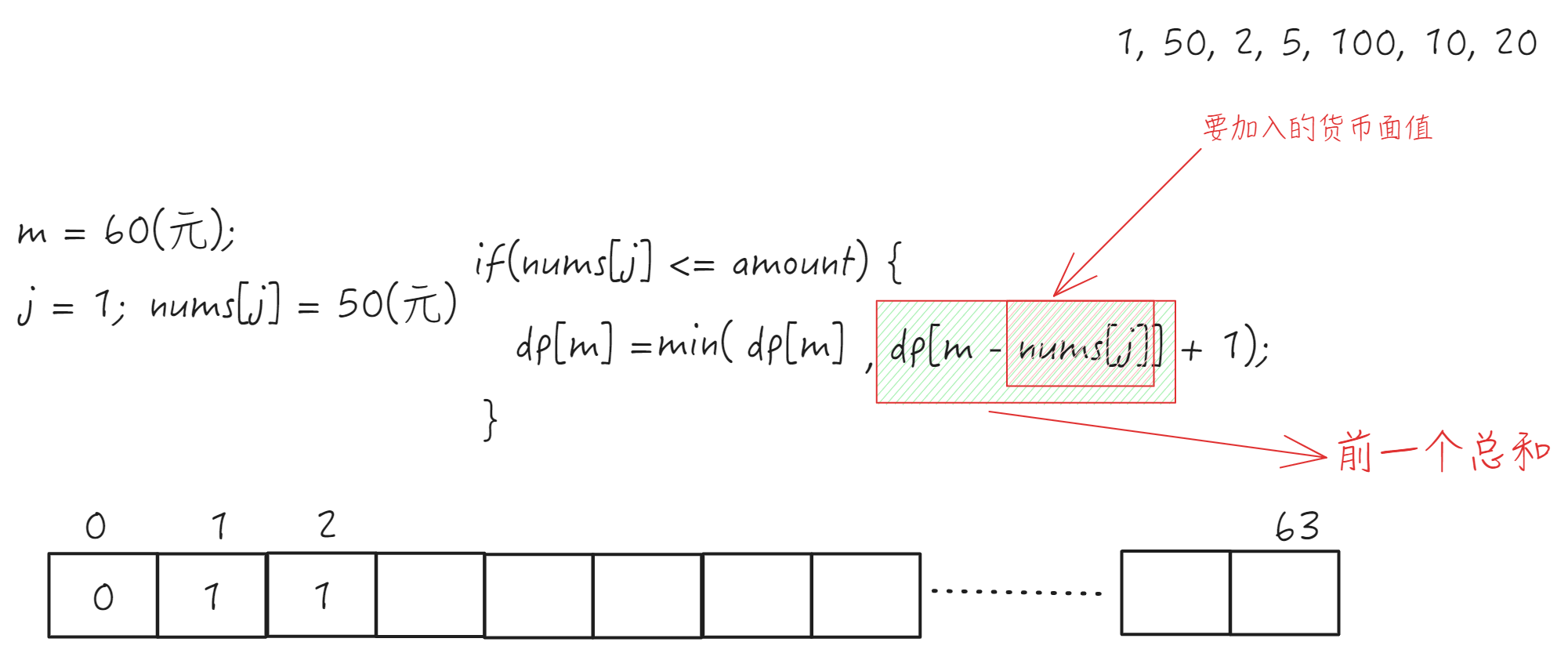
数据结构和算法-贪心算法01- 认识贪心
贪心算法 什么是贪心算法 一个贪心算法总是做出当前最好的选择,也就是说,它期望通过局部最优选择从而得到全局最优的解决方案。 ----《算法导论》 贪心算法(Greedy Method): 所谓贪心算法就是重复地(或贪婪地)根据一个法则挑选解的一部分。当挑选完毕…...

Bash Shell - 获取日期、时间
1. 使用date获取日期 以下代码将date的执行结果存储在today变量中。date 是获取日期和时间的命令。 选择使用 quotes()或$ #!/bin/bashtodaydate echo $todaytoday$(date) echo $today 2. 使用 Format 输出所需日期和时间 date FORMAT 2.1 "MM-DD-YY" 形式输出…...

runnable和callable区别和底层原理
确实,Runnable 可以直接通过 Thread 类来运行,而 Callable 不能直接用于创建和运行线程。Callable 和 Runnable 都是 Java 中用于定义异步任务的接口,但它们的用法和目的有所不同。 ### Runnable 和 Thread Runnable 是接口,它不返…...

Springboot 整合 Java DL4J 打造自然语言处理之语音识别系统
🧑 博主简介:CSDN博客专家,历代文学网(PC端可以访问:https://literature.sinhy.com/#/literature?__c1000,移动端可微信小程序搜索“历代文学”)总架构师,15年工作经验,…...

虚幻引擎5(UE5)学习教程
虚幻引擎5(UE5)学习教程 引言 虚幻引擎5(Unreal Engine 5,简称UE5)是Epic Games开发的一款强大的游戏引擎,广泛应用于游戏开发、影视制作、建筑可视化等多个领域。UE5引入了许多先进的技术,如…...

从0开始深度学习(26)——汇聚层/池化层
池化层通过减少特征图的尺寸来降低计算量和参数数量,同时增加模型的平移不变性和鲁棒性。汇聚层的主要优点之一是减轻卷积层对位置的过度敏感。 1 最大汇聚层、平均汇聚层 汇聚层和卷积核一样,是在输入图片上进行滑动计算,但是不同于卷积层的…...

兼职发薪系统:高效、便捷的劳务发薪解决方案
在快速发展的数字化时代,企业对于高效、便捷的薪酬发放和管理解决方案的需求日益增长。特别是对于兼职人员众多的企业,如何实现快速、准确的发薪,同时确保员工信息的安全与保密,成为了一个亟待解决的问题。今天,我们将…...

MySQL数据库单表查询习题
目录 数据内容介绍习题题目答案 数据内容介绍 数据库中有两个表 内容如下: 习题 题目 查询出部门编号为D2019060011的所有员工所有财务总监的姓名、编号和部门编号。找出奖金高于工资的员工。找出奖金高于工资40%的员工。找出部门编号为D2019090011中所有…...

多模态PaliGemma——Google推出的基于SigLIP和Gemma的视觉语言模型
前言 本文怎么来的呢?其实很简单,源于上一篇文章《π0——用于通用机器人控制的流匹配VLA模型:一套框架控制7种机械臂(改造了PaliGemma和ACT的3B模型)》中的π0用到了PaliGemma 故本文便来解读下这个PaliGemma 第一部分 PaliGemma 1.1 Pal…...

电路原理:电阻桥。
电路的基础是电阻电路。电阻电路有两种基本接线方法(串连和并连,二者有不同的解算与用法:串连分压、并连分流)。电阻电路就是使用基本接线方法的组合方案,其解算方法主要内容是判断好整体布局以及各个局部的串并连关系…...

实践出真知:MVEL表达式中for循环的坑
目录标题 背景MVEL脚本(有问题的)MVEL脚本(正确的)结论分析 背景 需要从一个URL的拼接参数中解析出id的值并输出 比如: 存在URLhttps://xxxxxxxxxx?id999999&type123&name345 然后需要输出id999999 MVEL脚本(有问题的) 入参:parseThisUrlhttp…...

Flutter运行App时出现“Running Gradle task ‘assembleDebug“问题解决
在参考了众多解决办法中最有用并且最快的方法 Gradle Distributions 在这个地方下载对应你这个文件中的gradle版本 然后将 最后一行本来不是这样的,我们把下载好的zip包保存到本地,然后用这个代替网址,最后成功运行...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
