数据结构-数组(稀疏矩阵转置)和广义表
目录
- 1、数组
- 定义
- 1)数组存储地址计算
- 示例
- ①行优先
- ②列优先
- 2)稀疏矩阵的转置
- 三元组顺序表
- 结构定义
- ①普通矩阵转置
- ②三元组顺序表转置稀疏矩阵
- ③稀疏矩阵的快速转置
- 3)十字链表
- 结构定义
- 2、广义表
- 定义
- 1)基本操作
- ①GetHead
- ②GetTail
- 2)构造存储结构的两种方法
- 表头表尾
- 结构定义
- 3)递归算法
- ①求广义表深度
- ②复制广义表
- ③创建广义表
1、数组
定义
数组是一种用于存储多个相同类型数据的集合,其元素在内存中连续存放并按照一定的顺序排列。这种有序性和连续性使得数组在访问时具有较高的效率。数组的特点包括所有元素具有相同的数据类型、可以通过索引快速访问任意元素、支持各种操作如遍历和排序等,并且数组的定义和初始化方式在不同编程语言中有所不同。
1)数组存储地址计算
数组存储地址的计算主要依赖于数组的起始地址、元素的数据类型(即每个元素所占的字节数)以及元素的下标位置
一维数组的存储地址计算
首元素地址:假设一维数组A的首地址为L,且每个元素占用C个字节。则数组中任意元素A[i]的地址可以通过公式Loc(A[i]) = L + i * C来计算。
示例:如果数组A的首地址是1000,每个元素占4个字节,那么A[3]的地址就是1000 + 3 * 4 = 1012。
二维数组的存储地址计算
行优先存储:在行优先存储中,二维数组的元素按照行的顺序依次存储。对于二维数组B[m][n],元素B[i][j]的地址计算公式为Loc(B[i][j]) = Loc(B[0][0]) + (i * n + j) * C,其中C是每个元素占用的字节数。
列优先存储:在列优先存储中,二维数组的元素按照列的顺序依次存储。对于二维数组B[m][n],元素B[i][j]的地址计算公式为Loc(B[i][j]) = Loc(B[0][0]) + (j * m + i) * C。
示例:假设有一个3x4的二维数组B,按行优先存储,首地址为1000,每个元素占2个字节。那么B[2][3]的地址就是1000 + (2*4 + 3) * 2 = 1026。
多维数组的存储地址计算
对于更高维度的数组,地址计算方法类似,只是需要考虑更多维度的索引和步长。
例如,按行优先存储的三维数组D[m][n][p]的元素D[i][j][k]的地址计算公式为Loc(D[i][j][k]) = Loc(D[0][0][0]) + ((i * n * p + j * p + k) * C)。
列优先:Loc(D[i][j][k]) = Loc(D[0][0][0]) + (knm+j*m+i)*C
示例
数组A[9][3][5][8],首地址为100,每个元素占4个字节,求a[8][2][4][7]的地址
①行优先
100+(8358+258+48+7)*4
②列优先
100+(7539+439+29+8)*4
2)稀疏矩阵的转置
三元组顺序表
由于稀疏矩阵中含有大量的零元素,空间利用率很低,所以需要三元组顺序表来表示稀疏矩阵中的非零元素,它通过行优先的顺序将非零元素及其位置信息存储在一个线性表中,节省存储空间并简化运算


结构定义
typedef struct{int i,j;//该非零元的行下标和列下标ElemType e;
}Triple;
typedef struct{Triple data[MAXSIZE + 1];//非零元三元组表,data[0]未用int mu,nu,tu;//矩阵的行数、列数和非零元总数
TSMatrix;
①普通矩阵转置
for(col = 1;col <= nu;++col)for(row = 1;row <= mu;++row)T[col][row] = M[row][col];
②三元组顺序表转置稀疏矩阵
Status TransposeSMatrix(TSMatrix M, TSMatrix &T){//采用三元组表存储表示,求稀疏矩阵M的转置矩阵TT.mu = M.nu; T.nu = M.mu; T.tu = M.tu;if(T.tu){q = 1;for(col = 1; col <= M.nu; ++col)for(p = 1; p <= M.tu; ++p)if(M.data[p].j == col){T.data[q].i = M.data[p].j; T.data[q].j = M.data[p].i;T.data[q].e = M.data[p].e; ++q;}}return OK;
}//TransposeSMatrix
③稀疏矩阵的快速转置
如果能预先确定就诊M中每一列(即T中的每一行)的第一个非零元在b.data中应有的位置,那么在对a.data中的三元组一次作转置时,便可直接放到b.data中恰当的位置上去,提高运算效率。
为此,需要附设num和cpot两个向量。num[col]表示矩阵M中第col列中非零元的个数,cpot[col]指示M中第col列的第一个非零元在b.data中的恰当位置。显然有
cpot[1] = 1;
cpot[col] = cpot[col - 1] + num[col - 1], 2 <= col <= a.nu

接下来就可以利用num和cpot向量快速确定转置后各元素在三元组表中的位置,提高运行效率
Status FastTransposeSMatrix(TSMatrix M, TSMatrix &T){//采用三元组顺序表存储表示,求稀疏矩阵M的转置矩阵TT.mu = M.nu; T.nu = M.mu; T.tu = M.tu;if(T.tu){for(col = 1; col <= M.nu; ++col)num[col] = 0;for(t = 1; t <= M.tu; ++t)++num[M.data[t].j];//求M中每一列含非零元个数cpot[1] = 1;//求第col列中第一个非零元在b.data中的序号for(col = 2; col <= M.nu; ++col)cpot[col] = cpot[col - 1] + num[col - 1];for(p = 1; p <= M.tu; ++p){col = M.data[p].j; q = cpot[col];T.data[q].i = M.data[p].j; T.data[q].j = M.data[p].i;T.data[q].e = M.data[p].e; ++cpot[col];//当一列的第一个元素转置完成后,下一个需要转置的是三元组表的下一个位置}//for}//ifreturn OK;
//FastTransposeSMatrix
3)十字链表
十字链表是一种用于表示稀疏矩阵的特殊存储结构,它通过行优先的顺序将非零元素及其位置信息存储在一个线性表中。每个节点包含五个字段:行号、列号、值、向下指针和向右指针,从而形成一个十字交叉的链表结构。这种结构不仅节省了存储空间,还提高了运算效率,并使得对稀疏矩阵的操作更加灵活和高效。

结构定义
typedef struct OLNode{int i,j;//该非零元的行和列下标ElemType e;struct OLNode *right,*down;//该非零元所在行表和列表的后继链域
}OLNode; *OLink;typedef struct{OLink *rhead,*chead;int mu,nu,tu;//稀疏矩阵的行数、列数、非零元总数
}CrossList;
2、广义表
定义
广义表是一种非线性的数据结构,它允许表中的元素既可以是单个数据项(原子),也可以是另一个广义表。这种结构使得广义表能够表示复杂的嵌套关系和层次结构。广义表的特点包括其元素的多样性(可以是原子或其他广义表)、结构的灵活性(可以嵌套任意深度)以及操作的复杂性(如求表头、表尾等)。在存储上,广义表通常采用链式结构来表示,以方便处理其复杂的嵌套关系。
1)基本操作
①GetHead
获取广义表的第一个元素,可以是原子,可以是列表
②GetTail
除了广义表中第一个元素的所有其他元素的集合,无论该元素是什么,都需要在外面额外套上一个(),即使是空表,或该值本来就有()
该部分主要是在给出一个广义表时能正确获取表头和表尾
2)构造存储结构的两种方法
表头表尾
结构定义
typedef struct GLNode{ElemTag tag;//公共部分,用于区分原子结点和表结点union{//原子结点和表结点的联合部分AtomType atom;//atom是原子结点的值域,AtomType由用户定义struct{struct GLNode *hp,*tp;}ptr;//ptr是表结点的指针域,ptr.hp和[tr.tp分别指向表头和表尾};
}*GList;//广义表类型
示例:
A = ()
B = (e)
C = (a,(b,c,d))
D = (A,B,C)
E = (a,E)//递归表 E = (a,(a,(a,…)))

另一种方法我还没理解,就不在这里说了
3)递归算法
由于广义表的定义本身就具有一定的递归性,且其子表问题与其本身的问题具有极高相似度、关联性,所有递归算法与广义表操作具有极好的适配性
①求广义表深度
int GListDepth(GList L){//采用头尾链表存储结构,求广义表L的深度。if C!L) return 1;// 空表深度1if (L—> tag == ATOM) return 0;// 原子深度 0for (max=0, pp=L; PP; pp=pp->ptr. tp) {dep = GListDepth(pp—>Ptr.hp);// 求以 pp—>ptr.hp 为头指针的子表深度if (dep > max) max = dep;}return max + 1;//非空表的深度是各元素的深度的最大值+1
}// GListDepth
②复制广义表
Status CopyGList(GList &T, GList L) {// 采用头尾链表存储结构,由广义表L复制得到广义表T。if(!L) T = NULL;// 复制空表else {if(!(T= (GList) malloc(sizeof(GL.Node))))exit(OVERFLOW);// 建表结点T -> tag = L -> tag;if (L—> tag == ATOM) T -> atom = L -> atom;// 复制单原子else {CopyGList(T-> ptr. hp, L->ptr. hp) ;// 复制广义表L->ptr.hp 的一个副本T->ptr.hpCopyGList(T—> ptr. tp, L->ptr. tp);// 复制广义表L->ptr.tp 的一个副本T->ptr.tp} // else} // elsereturn OK;
}// CopyGList
③创建广义表
三种情况:
- 带括弧的空白串
- 长度为1的单字符串
- 长度>1的字符串
显然,前两种情况为递归的终结状态,子表为空表或只含一个原子结点,后一种情况为递归调用
Status CreateGList (GList &L, SString S) {//采用头尾链表存储结构,由广义表的书写形式串S创建广义表L。设 emp="()"if (StrCompare(S, emp))L=NULL; //创建空表else {if (! (L = (GList) malloc (sizeof (GLNode)))) exit (OVERFLOW); //建表结点if (StrLength(S)==1){L->tag = ATOM; L->atom =S;}// 创建单原子广义表else {L->tag = LIST; p = L;SubString (sub, S, 2, Strength(S)—2) ;// 脱外层括号do{// 重复建n 个子表sever(sub,hsub);// 从 sub中分离出表头串hsubCreateGList(p->ptr. hp,hsub);q = p;if (!StrEmpty(sub)){// 表尾不空if (!(p = (GLode * ) malloc (sizeof (GLNode))))exit (OVERFLOW) ;p->tag = LIST; q->ptr.tp = p;}//if}while (! StrEmpty (sub)) ;q—>ptr. tp = NULL;}//else} // elsereturn OK;
}// CreateGListStatus sever(SString &str, SString &hstr) {// 将非空串 str 分割成两部分:hsub 为第一个‘,’之前的子串,str 为之后的子串n= StrLength(str); i=0;k=0;//k记尚未配对的左括号个数do {// 搜索最外层的第一个逗号++i;SubString(ch, str,i,1);if(ch =='(') 十十k;else if (ch==‘)’) --k;} while (i<n && (ch! =','|| k! =0));if (i<n){SubString (hstr, str, 1, i—1); SubString(str, str, i+1, n—i); } else {StrCopy (hstr, str); ClearString(str) }
} // sever
相关文章:

数据结构-数组(稀疏矩阵转置)和广义表
目录 1、数组定义 1)数组存储地址计算示例①行优先②列优先 2)稀疏矩阵的转置三元组顺序表结构定义 ①普通矩阵转置②三元组顺序表转置稀疏矩阵③稀疏矩阵的快速转置 3)十字链表结构定义 2、广义表定义 1)基本操作①GetHead②GetT…...

Java中的远程方法调用——RPC详解
1. 什么是RPC? RPC基础介绍 Java中的远程方法调用(Remote Procedure Call,RPC)是一种允许一个程序调用另一台计算机上方法的技术,就像在本地一样。RPC的核心思想是简化分布式计算,让我们可以跨网络调用远程…...

【kafka】大数据编写kafka命令使用脚本,轻巧简洁实用kafka
kafka是大数据技术中举足轻重的技术,市面上也有很多kafka的ui界面,但是都会占用比较大的内存和性能,这里我编写好了一个fakfa的脚本集成了kafka常见的命令使用。脚本资源放在文章顶部可自行拿取。 《Kafka 命令大全系统脚本使用指南》 在大数…...
)
交换区(Swap Area或Swap Partition)
在操作系统中,交换区(Swap Area或Swap Partition)扮演着至关重要的角色,主要用于在物理内存(RAM)不足时提供额外的虚拟内存空间。以下是交换区的主要功能和作用: 一、内存扩展 当系统的物理内…...

Excel 无法打开文件
Excel 无法打开文件 ‘新建 Microsoft Excel 工作表.xlsx",因为 文件格式或文件扩展名无效。请确定文件未损坏,并且文件扩展名与文件的格式匹配。...

MySQL —— Innodb 索引数据结构
文章目录 不用平衡二叉树或红黑树作为索引B树适合作为索引比B树更适合作为索引的结构——B树总结 MySQL 使用 B树索引数据结构(因为默认使用 innodb 存储引擎) B树:有序数组 平衡多叉树;B树:有序数组链表 平衡多叉树…...

探索C语言数据类型
目录 前言 一、基本数据类型 1.整型(Integer) 2.浮点型(Floating - point) 3.字符型(Character) 4.布尔型(Boolean) 二、派生数据类型 1.数组(Array)…...

凌晨官宣离婚,他们为何让老粉直呼天塌?
你说的是影视飓风MediaStorm的创始人Tim和小鱼吧,他们确实在11月5日凌晨官宣离婚了。以下是具体介绍:官宣离婚2024年11月5日凌晨,影视飓风MediaStorm的创始人Tim(潘天鸿)在社交媒体上发文,宣布与小鱼&#…...

Spring Boot 导出 Excel 文件
本文将详细介绍如何使用 Spring Boot 和 Apache POI 实现 Excel 文件的导出功能,帮助开发者快速上手。 1. 准备工作 首先,确保你的 Spring Boot 项目已成功创建并运行。接下来,需要在 pom.xml 文件中添加 Apache POI 相关依赖,以…...

HTTPSOK:SSL/TLS证书自动续期工具
HTTPSOK 是一个支持 SSL/TLS 证书自动续期 的工具,旨在简化 SSL 证书的管理,尤其是自动化处理证书续期的工作。对于大多数网站而言,SSL 证书的续期是一项必要但容易被忽视的工作,因为 SSL 证书的有效期通常为 90 天。使用 HTTPSOK…...
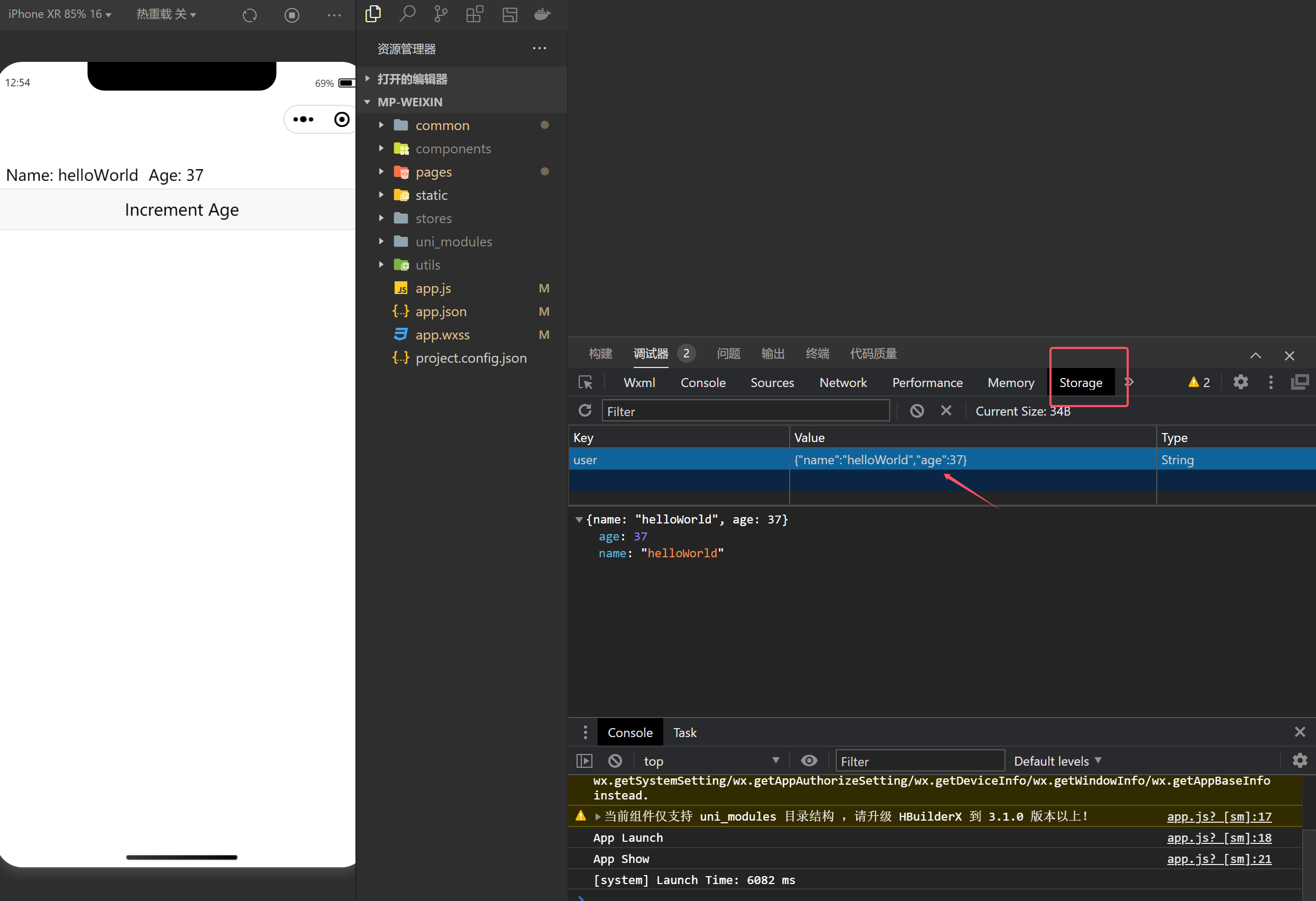
Uniapp安装Pinia并持久化(Vue3)
安装pinia 在uni-app的Vue3版本中,Pinia已被内置,无需额外安装即可直接使用(Vue2版本则内置了Vuex)。 HBuilder X项目:直接使用,无需安装。CLI项目:需手动安装,执行yarn add pinia…...

基于Dpabi和spm12的脑脊液(csf)分割和提取笔记
一、前言 脑脊液(csf)一直被认为与新陈代谢有重要关联,其为许多神经科学研究提供重要价值,从fMRI图像中提取脑脊液信号可用于多种神经系统疾病的诊断。特别是自2019年Science上那篇著名的csf-BOLD文章发表后,大家都试图…...

【每日一题】2012考研数据结构 - 求字符串链表公共后缀
本篇文章将为大家讲解一道关于链表的经典题目——求两个链表的共同后缀节点。该问题在实际开发中同样具有很大的应用价值,是每一位数据结构学习者不可错过的重要题目。 问题描述 假设我们有一个带头结点的单链表来保存单词,每个节点包含一个字符和指向…...
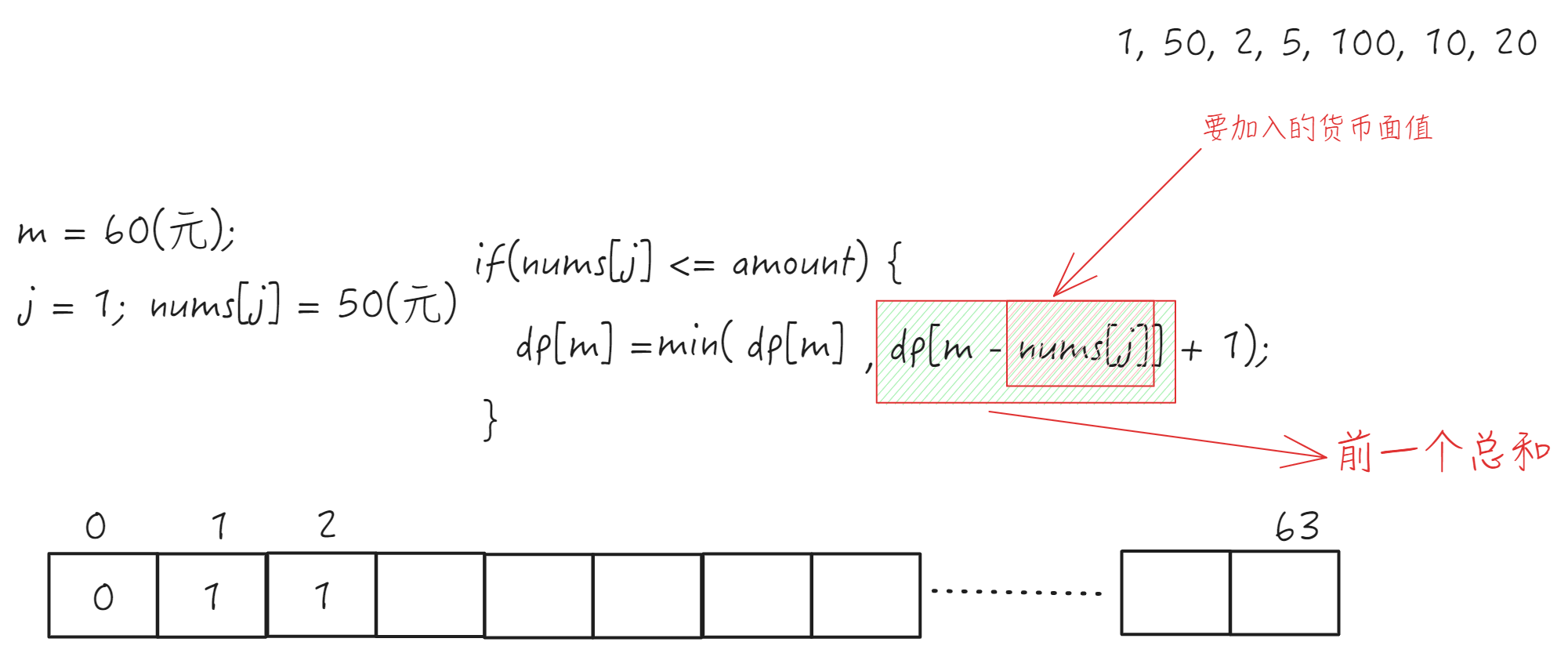
数据结构和算法-贪心算法01- 认识贪心
贪心算法 什么是贪心算法 一个贪心算法总是做出当前最好的选择,也就是说,它期望通过局部最优选择从而得到全局最优的解决方案。 ----《算法导论》 贪心算法(Greedy Method): 所谓贪心算法就是重复地(或贪婪地)根据一个法则挑选解的一部分。当挑选完毕…...

Bash Shell - 获取日期、时间
1. 使用date获取日期 以下代码将date的执行结果存储在today变量中。date 是获取日期和时间的命令。 选择使用 quotes()或$ #!/bin/bashtodaydate echo $todaytoday$(date) echo $today 2. 使用 Format 输出所需日期和时间 date FORMAT 2.1 "MM-DD-YY" 形式输出…...

runnable和callable区别和底层原理
确实,Runnable 可以直接通过 Thread 类来运行,而 Callable 不能直接用于创建和运行线程。Callable 和 Runnable 都是 Java 中用于定义异步任务的接口,但它们的用法和目的有所不同。 ### Runnable 和 Thread Runnable 是接口,它不返…...

Springboot 整合 Java DL4J 打造自然语言处理之语音识别系统
🧑 博主简介:CSDN博客专家,历代文学网(PC端可以访问:https://literature.sinhy.com/#/literature?__c1000,移动端可微信小程序搜索“历代文学”)总架构师,15年工作经验,…...

虚幻引擎5(UE5)学习教程
虚幻引擎5(UE5)学习教程 引言 虚幻引擎5(Unreal Engine 5,简称UE5)是Epic Games开发的一款强大的游戏引擎,广泛应用于游戏开发、影视制作、建筑可视化等多个领域。UE5引入了许多先进的技术,如…...

从0开始深度学习(26)——汇聚层/池化层
池化层通过减少特征图的尺寸来降低计算量和参数数量,同时增加模型的平移不变性和鲁棒性。汇聚层的主要优点之一是减轻卷积层对位置的过度敏感。 1 最大汇聚层、平均汇聚层 汇聚层和卷积核一样,是在输入图片上进行滑动计算,但是不同于卷积层的…...

兼职发薪系统:高效、便捷的劳务发薪解决方案
在快速发展的数字化时代,企业对于高效、便捷的薪酬发放和管理解决方案的需求日益增长。特别是对于兼职人员众多的企业,如何实现快速、准确的发薪,同时确保员工信息的安全与保密,成为了一个亟待解决的问题。今天,我们将…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...
