数据结构_哈夫曼树及其应用
构造算法的例子




构造算法的实现


初始化,置权值

int i, m, s1, s2;m = 2 * n - 1;for (i = 1; i <= m; i++){HT[i].lch = 0;HT[i].rch = 0;HT[i].parent = 0;}for (i = 1; i <= n; i++){cin >> HT[i].weight;}
合并结点

// 创建哈夫曼树for (i = n + 1; i <= m; i++){s1 = -1;s2 = -1;Selete(HT, i - 1, s1, s2);HT[s1].parent = i;HT[s2].parent = i;HT[i].lch = s1;HT[i].rch = s2;HT[i].weight = HT[s1].weight + HT[s2].weight;}
哈夫曼编码

void HuNode::create_Code(HuNode* HT, char** code, int n)
{int i, current, parent, k;char temp[100]; // 临时数组存放编码for (i = 1; i <= n; i++){current = i;parent = HT[i].parent;k = 0; // 编码长度计数器while (parent != 0){if (HT[parent].lch == current){temp[k] = '0'; // 左子节点编码为 '0'k++;}else{temp[k] = '1';k++;}current = parent;parent = HT[current].parent;}temp[k] = '\0';// 将编码倒置并保存code[i] = new char[k + 1];for (int j = 0; j < k; j++){code[i][j] = temp[k - j - 1];}code[i][k] = '\0';}
}文件的编码或译码


int HuNode::Decode(const string codestr, char txtstr[], int n)
{int index, root, i, curNode;index = 0;root = 2 * n - 1; // 根节点编号curNode = root;for (i = 0; i < codestr.length(); i++){if (codestr[i] == '0'){curNode = this[curNode].lch;}else{curNode = this[curNode].rch;}// 解码失败if (curNode == 0){return error;}// 是叶子节点if (this[curNode].lch == 0 && this[curNode].rch == 0){txtstr[index] = this[curNode].data;index++;curNode = root;}}if (curNode != root){return error;}txtstr[index] = '\0';return ok;
}
相关文章:

数据结构_哈夫曼树及其应用
构造算法的例子 构造算法的实现 初始化,置权值 int i, m, s1, s2;m 2 * n - 1;for (i 1; i < m; i){HT[i].lch 0;HT[i].rch 0;HT[i].parent 0;}for (i 1; i < n; i){cin >> HT[i].weight;}合并结点 // 创建哈夫曼树for (i n 1; i < m; i){s1…...
从0开始学习机器学习--Day19--学习曲线
一般来说,如果一个算法的表现不理想,那么多半是因为出现了欠拟合或过拟合问题,这种时候我们要做的就是搞清楚出现的是偏差问题还是方差问题,亦或是二者皆有,这有助于我们精准定位问题所在。 之前,我们发现…...

2.索引:深入解析 B+ 树:原理、MySQL 应用及与其他数据结构的对比
B 树是一种高效的平衡树结构,在数据库和文件系统中被广泛应用,尤其在 MySQL 中,InnoDB 存储引擎通过 B 树实现索引结构,提升了大数据量条件下的查询性能。 本文将深入介绍 B 树的原理和设计特点,分析 MySQL 中使用 B …...

[全网最细数据结构完整版]第六篇:3分钟带你吃透栈并模拟实现
目录 1->栈的概念和结构 1.1栈的概念 1.2栈的结构 2->栈的实现 2.1定义关于栈的结构体和各种函数 2.2栈的初始化 STInit 函数 2.3栈的销毁 STDestroy 函数 2.4栈的插入操作 STPush 函数 2.5栈的判断是否为空操作 STEmpty 函数 2.6栈的删除操作 STPop 函数 2.7…...

如何在 Docker 容器中启动 X11 图形界面程序
如何在 Docker 容器中启动 X11 图形界面程序 在使用 Docker 时,我们通常会发现,容器中的图形应用没法直接显示到宿主机的界面上。不过,我们可以通过共享 X11 的 Unix 套接字,让容器把显示数据传递给宿主机的 X11 服务器ÿ…...

pycharm保存是自动格式化
在PyCharm中设置保存时自动格式化代码,可以按照以下步骤进行: 1. 打开设置 在Windows和Linux系统中,可以通过File(文件)->Settings(设置)打开设置窗口;在Mac系统中,…...

.netCore WebAPI中字符串加密与解密
In today’s digital landscape, securing sensitive information is more critical than ever. If you’re using ASP.NET Core, you might store configuration settings in appsettings.json. However, hardcoding sensitive data like connection strings or API keys in p…...

Next.js + Move 石头剪刀布
rock-paper-scissors 写在前面 本地 源码:https://github.com/zcy1024/SuiStudy/tree/main/rock-paper-scissors # 或其它等价的命令来安装依赖并将项目跑起来 pnpm install pnpm run dev # http://localhost:3000/在线(如果没过期的话) …...

[面试]关于Redis 的持久化你了解吗
Redis的持久化是指Redis服务器在关闭或重启时,将内存中的数据保存到磁盘上的一种机制。Redis支持多种持久化方式。 一、RDB(Redis Database)持久化 RDB持久化是Redis默认采用的持久化方式,它将Redis在某个时间点的数据保存到磁盘上…...

Systemd:tmpfiles
Systemd提供了一个结构化的可配置方法来管理临时文件和目录,即systemd-tmpfiles,可以创建、删除和管理临时文件的服务。 $ systemctl list-units --all | grep systemd-tmpfilessystemd-tmpfiles-clean.service load…...

【Flutter 内嵌 android 原生 View以及相互跳转】
Flutter 内嵌 android 原生 View以及相互跳转 一. 内嵌android 原生View二、android 与 flutter 相互跳转 一. 内嵌android 原生View 在android 工程的包名下,也可在MainActivity创建 android 原生view ,继承PlatformView // 1.自定义textview public st…...

python externally-managed-environment 外部管理环境
https://realpython.com/python-virtual-environments-a-primer/?refyaolong.net#why-do-you-need-virtual-environments 简而言之, pip 默认会将您安装的所有外部包放置在 Python 安装路径/site-packages/ 的文件夹中一些Linux 和 macOS操作系统 预装了内部的 P…...
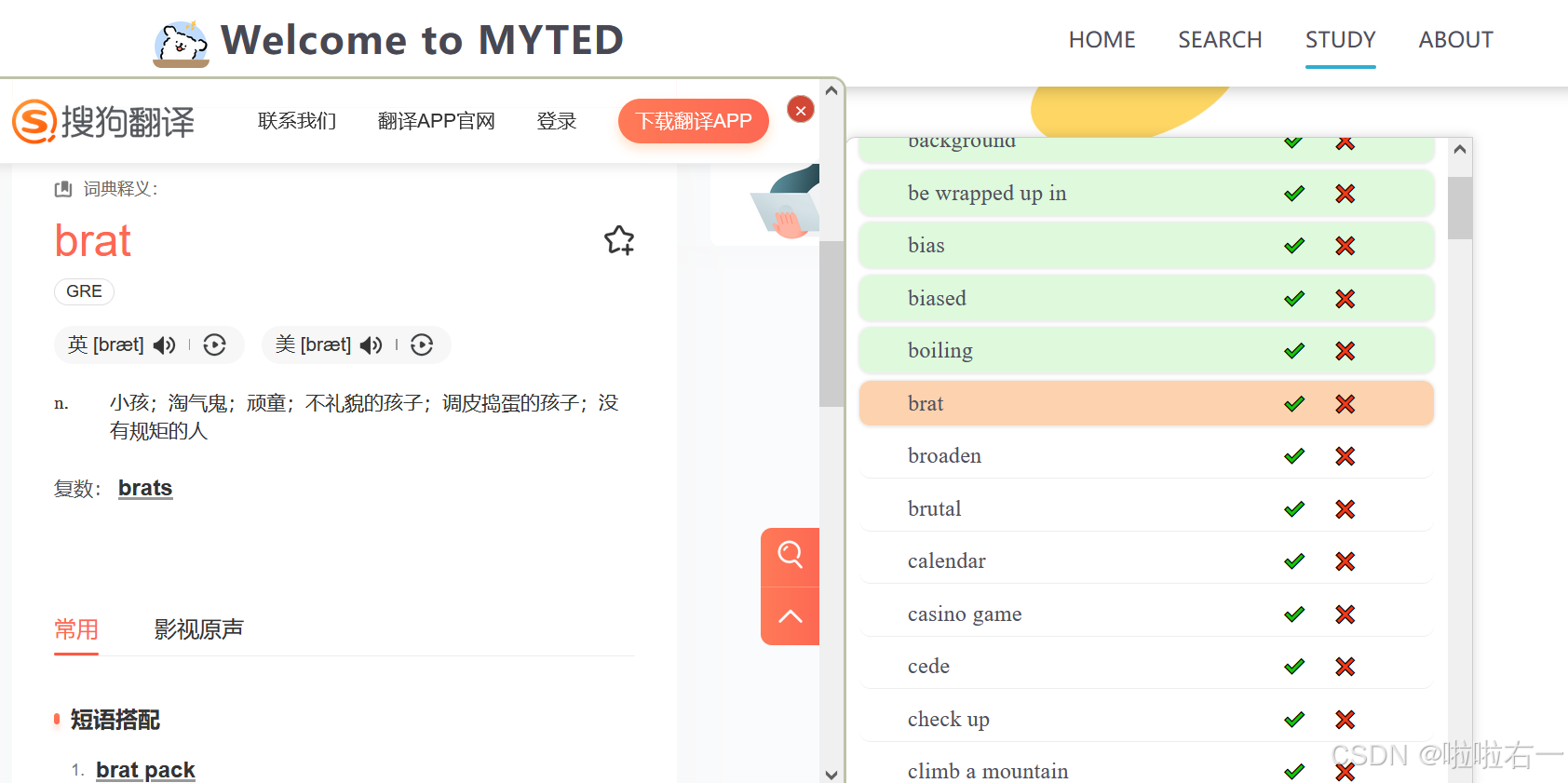
前端 | MYTED单篇TED词汇学习功能优化
文章目录 📚实现效果🐇before🐇after 📚模块实现解析🐇html🐇css🐇javascript 📚实现效果 🐇before 点击TED单篇词汇表按钮,选择对应TED打卡号,…...

64 mysql 的 表锁
前言 我们这里来说的就是 我们在 mysql 这边常见的 几种锁 行共享锁, 行排他锁, 表意向共享锁, 表意向排他锁, 表共享锁, 表排他锁 我们前面了解了行共享锁, 行排他锁, 表意向共享锁, 表意向排他锁 等等相关 我们这里 来看一下 表共享锁, 表排他锁 的获取, 以及 和 其他表级…...
)
【计网不挂科】计算机网络期末考试——【选择题&填空题&判断题&简述题】题库(1)
前言 大家好吖,欢迎来到 YY 滴计算机网络 系列 ,热烈欢迎! 本章主要内容面向接触过C的老铁 本博客主要内容,收纳了一部门基本的计算机网络题目,供yy应对期中考试复习。大家可以参考 欢迎订阅 YY滴其他专栏!…...

ajax关于axios库的运用小案例
AJAX案例 图书管理 四大功能: 展示图书删除图书编辑图书信息新增图书 步骤 1.bootstrap弹窗来实现新增和编辑图书时出现的弹窗 有两种方案: a.可以用自带的属性来进行弹窗的显示和隐藏 b.可以通过JS进行控制,此操作可以进行自定义&am…...
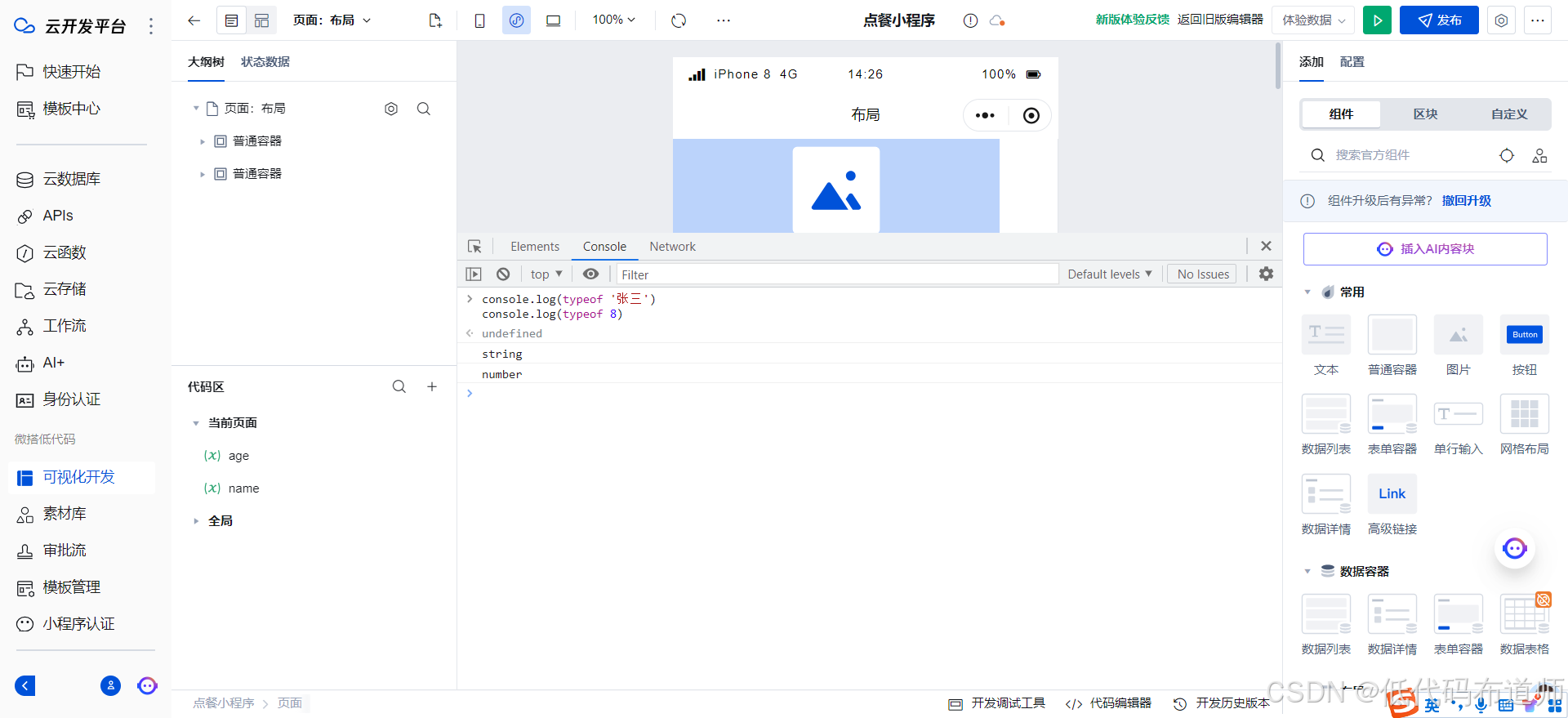
微搭低代码入门01变量
目录 1 变量的定义2 变量的赋值3 变量的类型4 算术运算符5 字符串的连接6 模板字符串7 检查变量的类型8 解构赋值8.1 数组的解构赋值8.2 对象的解构赋值 9 类型转换9.1 转换为字符串9.2 转换为数字9.3 转换为布尔值 总结 好些零基础的同学,在使用低代码的时候&#…...
盘点2024年10款视频剪辑,哪款值得pick!!
在这个短视频盛行的时代,如何让我们的故事更生动有趣呢?那就要对短视频进行修饰了。这就需要借助视频剪辑工具:而一款好的工具不仅仅是视频的“美颜”,更是创意的灵魂所在!想象一下,运用一款功能齐全的剪辑…...
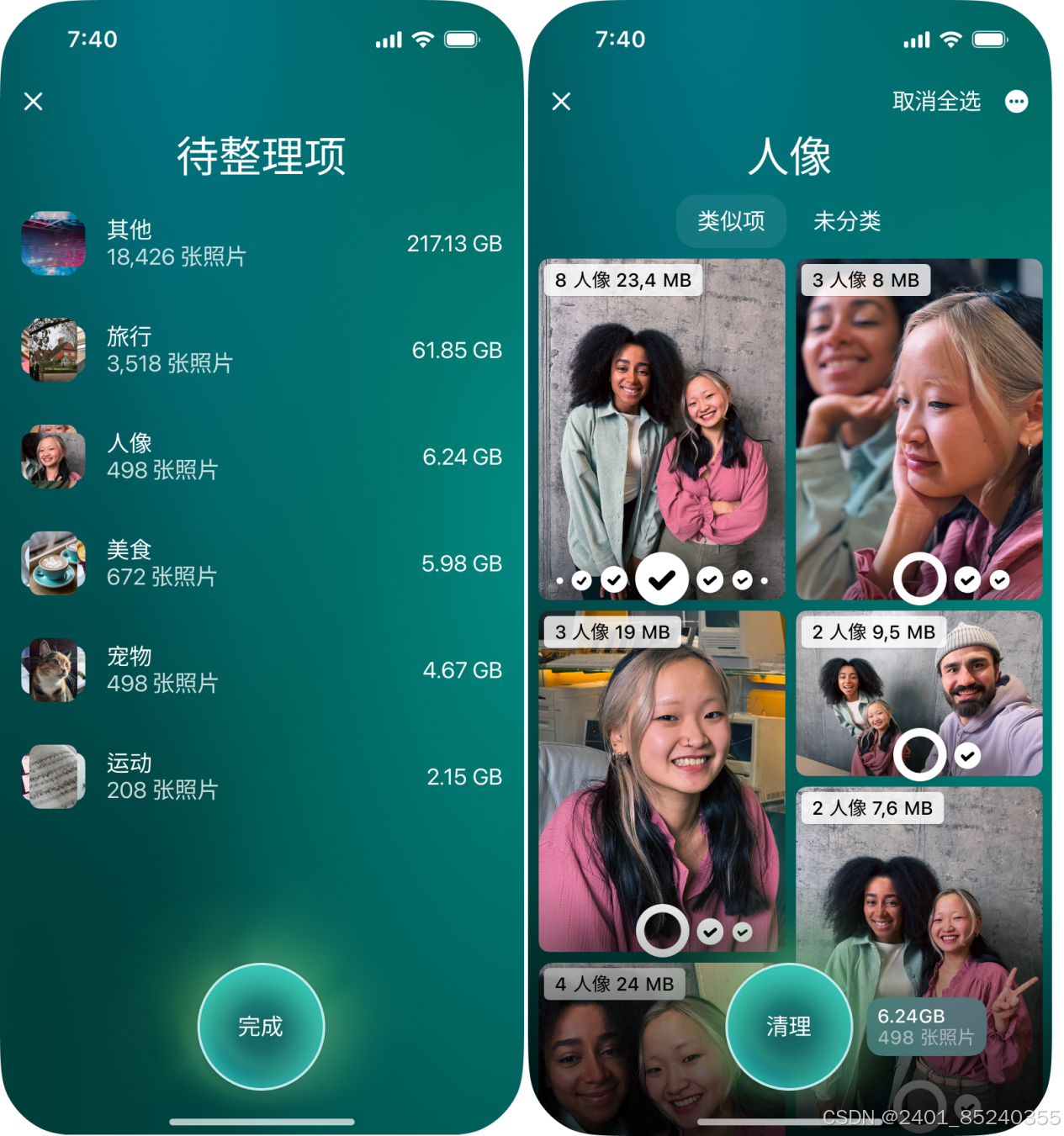
苹果手机照片批量删除:一键清理,释放空间
在数字化时代,iPhone不仅是我们沟通的桥梁,也是记录生活的重要工具。然而,随着时间的积累,手机中的照片数量不断增加,不仅占用大量存储空间,也让设备变得缓慢。苹果手机照片批量删除成为了一个普遍的需求。…...

《AI 大模型:重塑软件开发新生态》
《AI 大模型:重塑软件开发新生态》 一、AI 大模型引领软件开发新潮流二、AI 大模型在软件开发中的优势(一)提高开发效率(二)减少错误与提升质量(三)激发创新与拓展功能 三、AI 大模型在软件开发…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...
