【代码随想录day25】【C++复健】491.递增子序列;46.全排列;47.全排列 II;51. N皇后;37. 解数独
491.递增子序列
本题做的时候除了去重逻辑之外,其他的也勉强算是写出来了,不过还是有问题的,总结如下:
1 本题的关键:去重
与其说是不知道用什么去重,更应该说是完全没想到本题需要去重,说明这种题光靠干想还是不太行的。
要想去重,本质上还是要想明白什么情况会发生重复。对于本题来说,就是在同一个循环内,相同的数出现第二次的时候。
在递归生成子序列的过程中,代码中的每个循环代表一次“选择”操作。在同一层循环内,两个相同的数被选择所形成的结果是相同的,尽管它们可能出现在不同的位置,但生成的子序列完全一致。如果在同一层循环中选择了两个相同的数,那么这两个数选择后生成的子序列将发生重复。

还有最后一个问题,为什么是哈希表?
我们前面也有说过,发生重复的情况就是同一循环内相同的数出现两次。那看一个数出没出现过的最快的方法?当然就是哈希了。
2 分治问题
这个题倒是学会分治了,把递增的判断专门写了一个函数,但其实每次只要和vector的尾部判断就行了,完全不需要写一个函数,属于是ptsd了,然后就没去细想,另外也可以说是没想明白递归就可以完美解决递增判断的问题。
3 对于递归当中每个部分的作用的不熟悉
一开始写for循环的时候写成了这样:
for(int i=startindex; i<nums.size(); i++){path.push_back(nums[i]);if(isup(path)){result.push_back(path);}all(nums, i+1, path, result);path.pop_back();all(nums, i+1, path, result);}没去重是一方面,还写了两遍递归,当时想法是每次循环,每个值有取或者不取两个选项,所以取一个递归,不取一个递归。但不取的那个递归其实是在下一个for循环里涵盖了的,加上了才是多余的。
class Solution {
public:vector<vector<int>> findSubsequences(vector<int>& nums) {int startindex = 0;vector<vector<int>> result;vector<int> path;all(nums, startindex, path, result);return result;}void all(vector<int>& nums, int startindex, vector<int>& path, vector<vector<int>>& result){if(startindex == nums.size()){return ;}unordered_set<int> used;for(int i=startindex; i<nums.size(); i++){if (used.find(nums[i]) != used.end()) continue;path.push_back(nums[i]);used.insert(nums[i]);if(isup(path)){result.push_back(path);}all(nums, i+1, path, result);path.pop_back();//all(nums, i+1, path, result);}}bool isup(const vector<int>& path){int n = path.size();if(n < 2){return false;}int max = -101;for(int i=0; i<n; i++){if(path[i] >= max){max = path[i];}else{return false;}}return true;}
};可以看到我上面的代码还是很麻烦的,不仅体现在代码量上,还有计算量其实也比只判断队尾元素要大上不少。
46.全排列
这个题想的时候想了半天怎么去判断一个数组当中的各个元素有没有被用过。最终我想到的办法是一个二维数组,第一个维度是每个元素,第二个维度是对应它们有没有被使用过。想好之后直接去看了解析(因为我觉的我这个肯定想复杂了)一看果然如此,第一个维度完全没有必要,直接用下标就可以把值和用没用过的两个数组进行对应。
在看完解析之后写代码也是没遇到太大的问题的,就是还是在判断结束条件的时候写的复杂了一点:
bool allused = true;for(int i=0; i<nums.size(); i++){if(used[i]==1){allused = false;break;}}直接定义了一个布尔值来判断每个元素是否都被用过了,但其实不必如此,其实我后来也想明白了并且注释掉了,改成了判断path的长度和nums是否一致,这个才是更简洁更快的办法。
class Solution {
public:vector<vector<int>> permute(vector<int>& nums) {vector<int> used(nums.size());vector<int> path;vector<vector<int>> result;all(nums, used, path, result);return result;}void all(vector<int>& nums, vector<int>& used, vector<int>& path, vector<vector<int>>& result){// bool allused = true;// for(int i=0; i<nums.size(); i++){// if(used[i]==1){// allused = false;// break;// }// }if(path.size() == nums.size()){result.push_back(path);return;}for(int i=0; i<nums.size(); i++){if(used[i]==1){continue;}path.push_back(nums[i]);used[i] = 1;all(nums, used, path, result);path.pop_back();used[i] = 0;}}
};47.全排列 II
本题也是差点一遍做出来,不过对于去重的判断还是不够理解,所以导致一遍并没有成功。
首先,我们也要先理解为什么这道题在什么情况下会发生重复。
一开始没有细想,写了一个if(i>0 && nums[i] == nums[i-1]),但这个的意思是说,只要相同的出现第二回就视为重复。但实际情况是,我先输入一个1,然后再来一个1,这个时候的11和只有一个1显然是不同的,所以我又想,应该再加一个条件,那就是前一个元素没被用过,也就是used[i-1]==false。加上之后就成功通过了,但卡哥的used[i - 1] == true 也行,used[i - 1] == false 也行有给我干懵了,如果是true的情况下,又是什么逻辑?
冥思苦想很久之后去看了解析,看完之后沉默了。因为虽然说了很多树层树枝去重什么的,但感觉是在从结果上反推的,如果不画出图来根本不知道true的情况是怎么一个运作逻辑,所以个人认为就按false这个来会比较好。
class Solution {
public:vector<vector<int>> permuteUnique(vector<int>& nums) {sort(nums.begin(), nums.end());vector<vector<int>> result;vector<int> path;vector<int> used(nums.size());permute(nums, used, result, path);return result;}void permute(vector<int>& nums, vector<int>& used, vector<vector<int>>& result, vector<int>& path){if(path.size() == nums.size()){result.push_back(path);return;}for(int i=0; i<nums.size(); i++){if(used[i] == 1){continue;}if(i>0 && nums[i] == nums[i-1] && used[i-1] == false){continue;}used[i] = 1;path.push_back(nums[i]);permute(nums, used, result, path);path.pop_back();used[i] = 0;}}
};51. N皇后
这个题其实对我的意义还是很特殊的。
在我还是一个懵懂无知的大一少年时,一道n皇后粉碎了我的ACM梦。
冥思苦想许久后,一顿操作猛如虎,一看过了5%。
依然记得当时我在草稿纸上画棋盘格,试图找到答案组成的数组规律的狼狈样子(当时那个题好像是问n*n格有多少种方法,比这个可能简单一点?)...
后面和同学去抱怨,却得到了“这个题很经典,你应该会”的回答。
现在已经是能把这个题做出来的人了,回想同学的话,很有道理,但是我却有些会错了意。
题目很“经典”,所以不会做的我很“废材”,这样的逻辑关系是不存在的。因为对于我来说,这个题我没有见过,所以它不是经典题,而是一个全新的,并且很难的题,这样的题,或者哪怕是一个很简单很简单的题,只要我没做过,我都有不会的权力。“应该会”这个词背后的意义是“去了解”,而不是“不会的话,你就很废”,可惜我到现在才想明白。
不过总之,现在做完了这道题的我,也算是迈出那一步了吧。
class Solution {
public:vector<vector<string>> solveNQueens(int n) {vector<string> chessboard;string str = "";for(int i=0; i<n; i++){str += ".";}for(int i=0; i<n; i++){chessboard.push_back(str);}int row = 0;vector<vector<string>> result;backtracking(chessboard, n, row, result);return result;}void backtracking(vector<string>& chessboard, int n, int row, vector<vector<string>>& result){if(row == n){result.push_back(chessboard);return;}for(int i = 0; i < n; i++){if(isvalid(row, i, chessboard, n)){chessboard[row][i] = 'Q';backtracking(chessboard, n, row+1, result);chessboard[row][i] = '.';}}}bool isvalid(int row, int col, vector<string>& chessboard, int n){int yoko = row - 1;int tate = col - 1;while(yoko >=0 && tate>=0){if(chessboard[yoko][tate] == 'Q'){return false;}yoko--;tate--;}yoko = row - 1;tate = col + 1;while(yoko >= 0 && tate < n){if(chessboard[yoko][tate] == 'Q'){return false;}yoko--;tate++;}yoko = row - 1;tate = col;while(yoko>=0){if(chessboard[yoko][tate] == 'Q'){return false;}yoko--;}return true;}
};哪怕现在刷完回溯,以及前面那么多部分的题,再来看这个N皇后,都绝对没法说这是一个简单的题目。就像我在看完解析之后依然遇到了不少的问题:
1 二维棋盘的初始化方法
我写的这么多代码:
vector<string> chessboard;string str = "";for(int i=0; i<n; i++){str += ".";}for(int i=0; i<n; i++){chessboard.push_back(str);}其实用这一句:
vector<string> chessboard(n, string(n, '.'));
就可以等效了。
那为什么没写出来呢,鉴定为对于构造函数的不熟悉,无论是string还是vector都能用类似这种构造方式。

2 写判断的时候行和列没搞清楚
写的列判断写成了行判断,并且右上对角线写成了左下对角线。这个也是对二维数组不熟悉导致的,还需要多练多熟悉。
37. 解数独
看了解析视频之后做的,不过还是遇到了一点麻烦:
1 传参给isvalid的时候没像卡哥一样传一个值和board,而是把值先插入board之后再传的。这样看似差不多,实则是个超级大麻烦:横着竖着和九宫格必须跳过i,j位置所对应的元素,极其麻烦,横着竖着尚可以分成两段,九宫格直接不知道怎么写了。
2 其实如果传val也不太知道就功能怎么处理,差点就用枚举法了。像这种先/3再乘3是很聪明的处理方式:int startRow = (row / 3) * 3;
并且还知道了这样写会变成离row最近的3的倍数,而不是变成row。也就是每个中间步都仍然是int。
class Solution {
public:void solveSudoku(vector<vector<char>>& board) {backtracking(board);}bool backtracking(vector<vector<char>>& board){for(int i = 0; i < board.size(); i++){for(int j = 0; j < board[0].size(); j++){if(board[i][j] == '.'){for(char p = '1'; p <= '9'; p++){if(isvalid(board, i, j, p)){board[i][j] = p;if(backtracking(board)){return true;}board[i][j] = '.';}}return false;}}}return true;}bool isvalid(vector<vector<char>>& board, int row, int col, int val){for(int i = 0; i < row; i++){if(board[i][col] == val){return false;}}for(int i = 8; i > row; i--){if(board[i][col] == val){return false;}}for(int j = 0; j < col; j++){if(board[row][j] == val){return false;}}for(int j = 8; j > col; j--){if(board[row][j] == val){return false;}}int startRow = (row / 3) * 3;int startCol = (col / 3) * 3;for (int i = startRow; i < startRow + 3; i++) {for (int j = startCol; j < startCol + 3; j++) {if (board[i][j] == val) {return false;}}}return true;}
};写的还是麻烦了的,不过太困了,就不优化了。
相关文章:

【代码随想录day25】【C++复健】491.递增子序列;46.全排列;47.全排列 II;51. N皇后;37. 解数独
491.递增子序列 本题做的时候除了去重逻辑之外,其他的也勉强算是写出来了,不过还是有问题的,总结如下: 1 本题的关键:去重 与其说是不知道用什么去重,更应该说是完全没想到本题需要去重,说明…...

AI智能识物(微信小程序)
AI智能识物,是一款实用的小程序。可以拍照智能识物,可识别地标、车型、花卉、植物、动物、果蔬、货币、红酒、食材等等,AI智能技术识别准确度高。 更新说明: 此源码为1.2.0版本。 主要更新内容:新增security.imgSec…...

游戏引擎学习第三天
视频参考:https://www.bilibili.com/video/BV1XTmqYSEtm/ 之前的程序不能退出,下面写关闭窗体的操作 PostQuitMessage 是 Windows API 中的一个函数,用于向当前线程的消息队列发送一个退出消息。其作用是请求应用程序退出消息循环,通常用于处…...
帝国CMS7.5仿模板堂柒喜模板建站网 素材资源下载站源码
环境要求:phpmysql、支付伪静态 本套模板采用帝国cms7.5版UTF-8开发,一款非常不错的高端建站源码模板, 适用于中小型网络建站工作室源码模板下载站,支持自定义设置会员组。 源码下载:https://download.csdn.net/down…...
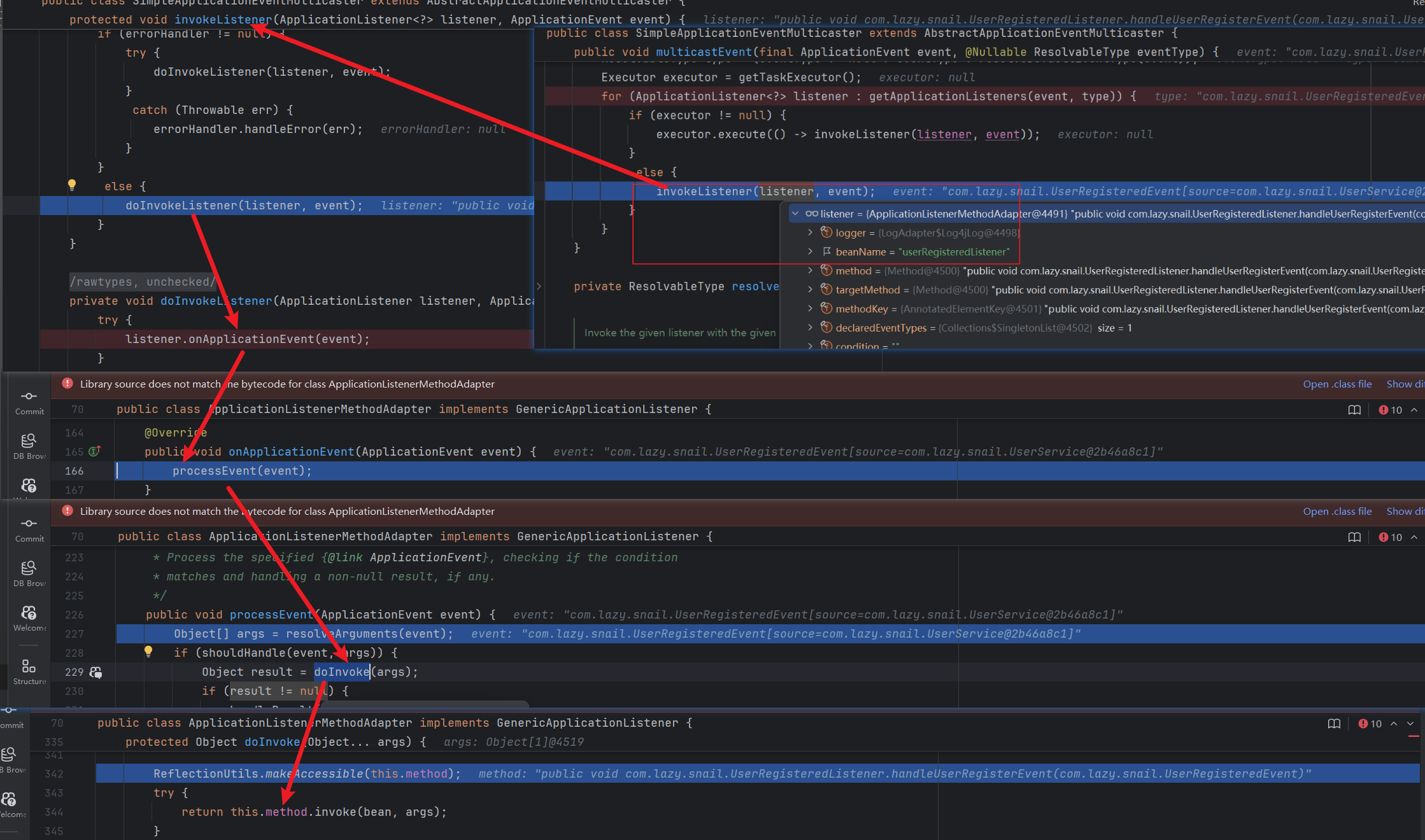
聊一聊Spring中的自定义监听器
前言 通过一个简单的自定义的监听器,从源码的角度分一下Spring中监听的整个过程,分析监听的作用。 一、自定义监听案例 1.1定义事件 package com.lazy.snail;import lombok.Getter; import org.springframework.context.ApplicationEvent;/*** Class…...
【王木头】最大似然估计、最大后验估计
目录 一、最大似然估计(MLE) 二、最大后验估计(MAP) 三、MLE 和 MAP 的本质区别 四、当先验是均匀分布时,MLE 和 MAP 等价 五、总结 本文理论参考王木头的视频: 贝叶斯解释“L1和L2正则化”ÿ…...

智谱AI视频生成模型CogVideoX v1.5开源 支持5/10秒视频生成
今日,智谱技术团队发布了其最新的视频生成模型 CogVideoX v1.5,并将其开源。这一版本是自8月以来,智谱技术团队推出的 CogVideoX 系列中的又一重要进展。 据了解,此次更新大幅提升了视频生成能力,包括支持5秒和10秒的视…...

算法(第一周)
一周周五,总结一下本周的算法学习,从本周开始重新学习许久未见的算法,当然不同于大一时使用的 C 语言以及做过的简单题,现在是每天一题 C 和 JavaScript(还在学,目前只写了一题) 题单是代码随想…...

Linux服务器进程的控制与进程之间的关系
在 Linux 服务器中,进程控制和进程之间的关系是系统管理的一个重要方面。理解进程的生命周期、控制以及它们之间的父子关系对于系统管理员来说至关重要。以下是关于进程控制、进程之间的关系以及如何管理进程的详细介绍: 1. 进程的概念 进程࿰…...

机器学习Housing数据集
import pandas as pd import seaborn as sns import matplotlib.pyplot as plt from sklearn.datasets import fetch_openml 设置Seaborn的美观风格 sns.set(style“whitegrid”) Step 1: 下载 Housing 数据集,并读入计算机 def load_housing_data(): housing …...

随着最新的补丁更新,Windows 再次变得容易受到攻击
SafeBreach专家Alon Leviev发布了一款名为 Windows Downdate的工具,可用于对Windows 10、Windows 11 和 Windows Server 版本进行降级攻击。 这种攻击允许利用已经修补的漏洞,因为操作系统再次容易受到旧错误的影响。 Windows Downdate 是一个开源Pyth…...

【Python】爬虫通过验证码
1、将验证码下载至本地 # 获取验证码界面html url http://www.example.com/a.html resp requests.get(url) soup BeautifulSoup(resp.content.decode(UTF-8), html.parser)#找到验证码图片标签,获取其地址 src soup.select_one(div.captcha-row img)[src]# 验证…...
dc-aichat(一款支持ChatGPT+智谱AI+讯飞星火+书生浦语大模型+Kimi.ai+MoonshotAI+豆包AI等大模型的AIGC源码)
dc-aichat 一款支持ChatGPT智谱AI讯飞星火书生浦语大模型Kimi.aiMoonshotAI豆包AI等大模型的AIGC源码。全网最易部署,响应速度最快的AIGC环境。PHP版调用各种模型接口进行问答和对话,采用Stream流模式通信,一边生成一边输出。前端采用EventS…...

检索增强生成
检索增强生成 检索增强生成简介 检索增强生成(RAG)旨在通过检索和整合外部知识来增强大语言模型生成文本的准确性和丰富性,其是一个集成了外部知识库、信息检索器、大语言模型等多个功能模块的系统。 RAG 利用信息检索、深度学习等多种技术…...

操作系统--进程
2.1.1 进程的概念、组成、特征 进程的概念 进程的组成 进程的特征 总结 2.1.2 进程的状态与转换,进程的组织 创建态、就绪态 运行态 阻塞态 终止态 进程状态的转换 进程的组织 链式方式 索引方式 2.1.3 进程控制 如何实现进程控制? 在下面的例子,将PCB2的是state设为1和和把…...

abap 可配置通用报表字段级日志监控
文章目录 1.功能需求描述1.1 功能1.2 效果展示2.数据库表解释2.1 表介绍3.数据库表及字段3.1.应用日志数据库抬头表:ZLOG_TAB_H3.2.应用日志数据库明细表:ZLOG_TAB_P3.3.应用日志维护字段配置表:ZLOG_TAB_F4.日志封装类5.代码6.调用方式代码7.调用案例程序demo1.功能需求描述 …...

OpenCV视觉分析之目标跟踪(11)计算两个图像之间的最佳变换矩阵函数findTransformECC的使用
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 根据 ECC 标准 78找到两幅图像之间的几何变换(warp)。 该函数根据 ECC 标准 ([78]) 估计最优变换(warpMatri…...

PGMP-串串0203 项目集管理绩效域战略一致性
1.项目集管理绩效域 2.战略一致性 战略一致性包含内容商业论证BC项目集章程项目集路线图环境评估项目集风险管理策略 前期formulation sub-phaseplanning sub-phase组织的战略计划项目集风险管理策略项目集管理计划商业论证BC项目集章程项目集路线图环境评估...

HiveMetastore 的架构简析
HiveMetastore 的架构简析 Hive Metastore 是 Hive 元数据管理的服务。可以把元数据存储在数据库中。对外通过 api 访问。 hive_metastore.thrift 对外提供的 Thrift 接口定义在文件 standalone-metastore/src/main/thrift/hive_metastore.thrift 中。 内容包括用到的结构体…...

【WRF模拟】全过程总结:WPS预处理及WRF运行
【WRF模拟】全过程总结:WPS预处理及WRF运行 1 数据准备1.1 嵌套域设置(Customize domain)-基于QGis中gis4wrf插件1.2 静态地理数据1.2.1 叶面积指数LAI和植被覆盖度Fpar(月尺度)1.2.2 地面反照率(月尺度)1.2.3 土地利用类型+不透水面积1.2.4 数据处理:geotiff→tiff(W…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
