力扣.167 两数之和 II two-sum-ii
数组系列
力扣数据结构之数组-00-概览
力扣.53 最大子数组和 maximum-subarray
力扣.128 最长连续序列 longest-consecutive-sequence
力扣.1 两数之和 N 种解法 two-sum
力扣.167 两数之和 II two-sum-ii
力扣.170 两数之和 III two-sum-iii
力扣.653 两数之和 IV two-sum-IV
力扣.015 三数之和 three-sum
力扣.016 最接近的三数之和 three-sum-closest
力扣.259 较小的三数之和 three-sum-smaller
题目
给你一个下标从 1 开始的整数数组 numbers ,该数组已按 非递减顺序排列,请你从数组中找出满足相加之和等于目标数 target 的两个数。
如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 <= index1 < index2 <= numbers.length 。
以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。
你可以假设每个输入 只对应唯一的答案 ,而且你 不可以 重复使用相同的元素。
你所设计的解决方案必须只使用常量级的额外空间。
示例 1:
输入:numbers = [2,7,11,15], target = 9 输出:[1,2] 解释:2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。
示例 2:
输入:numbers = [2,3,4], target = 6 输出:[1,3] 解释:2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。
示例 3:
输入:numbers = [-1,0], target = -1 输出:[1,2] 解释:-1 与 0 之和等于目标数 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。
提示:
2 <= numbers.length <= 3 * 10^4
-1000 <= numbers[i] <= 1000
numbers 按 非递减顺序 排列
-1000 <= target <= 1000
仅存在一个有效答案
前言
这道题和 leetcode 的第一道题非常类似,看起来非常简单。
不过今天回头看,解法还是很多的。
大概可以有下面几种:
暴力解法
数组排序+二分
HashSet/HashMap 优化
v1-暴力解法
思路
直接两次循环,找到符合结果的数据返回。
这种最容易想到,一般工作中也是我们用到最多的。
实现
注意:这里的下标从1开始。一看就不是一个面向程序员的题目。
class Solution {public int[] twoSum(int[] nums, int target) {int[] res = new int[2];final int n = nums.length;for(int i = 0; i < n; i++) {for(int j = i+1; j < n; j++) {if(nums[i] + nums[j] == target) {res[0] = i+1;res[1] = j+1;}}}return res;}
}效果
超出时间限制 21 / 24 个通过的测试用例
小结
暴力算法虽然容易想到,不过如果遇到特别长的场景用例,会直接超时。
我们如何改进一下呢?
排序是这个场景另一种很有用的方式。
v2-排序+二分
思路
我们希望排序,然后通过二分法来提升性能。
这里就发现,题目已经帮我排序好了。所以第一题的麻烦的部分全部省略了。
代码
class Solution {public int[] twoSum(int[] nums, int target) {final int n = nums.length;for(int i = 0; i < n; i++) {int other = target - nums[i];int j = binarySearch(nums, other, i+1);if(j >= 0) {return new int[]{i+1, j+1};}}return new int[]{-1, -1};}private int binarySearch(int[] nums,int target,int startIx) {int left = startIx;int right = nums.length-1;while (left <= right) {int mid = left + (right - left) / 2;int val = nums[mid];if(val == target) {return mid;}if(val > target) {right = mid-1;} else {left = mid+1;}}return -1;}
}效果
4ms 16.87%
嗯?
这个竟然不是本题目的最佳解法吗?
v3-HashMap
思路
在我们写完上面的写法之后,有没有一种感觉?
既然是要找另一部分的值,那么直接 Hash,复杂度 O(1) 不是更快?
是的,你真是个小机灵鬼。
哈希在这种等于的场景是最快的,不过上面的二分适用性更广一些,比如查询大于或者小于的时候。
当然本体限制了,必须常量的空间,所以这种解法被限制了,不过也值得看一下。
我们先来看一下哈希的解法。
代码
注意:这里的顺序要求有序,所以返回的时候和 T1 要反过来。
class Solution {public int[] twoSum(int[] nums, int target) {int n = nums.length;HashMap<Integer, Integer> hashMap = new HashMap<>();for(int i = 0; i < n; i++) {int other = target - nums[i];if(hashMap.containsKey(other)) {int j = hashMap.get(other);return new int[]{j+1, i+1};}// 存储hashMap.put(nums[i], i);}return new int[]{-1, -1};}
}效果
7ms 6.01%
只能说性能很差,猜测是 map 构建导致的耗时,不然这个作为 O(n) 的解法一定性能更好才对。
说明这一题一定有更加适合的解法。
v4-双指针
思路
其实在 v2 二分法的排序思路上,我们可以受到一些启发。
排序+二分是我们非常老实的一次遍历,然后再二分查找,复杂度为 n*log(n)
那么有没有可能在有序的数组中不用这么麻烦?
那就要说到巧妙的双指针了。
双指针
我们定义两个指针
left=0
right=n-1
sum=num[left]+num[right-1]因为数组有有序的,所以只有 3 种情况:
sum == target 直接满足
sum < target,left++
sum > target, right--
代码
class Solution {public int[] twoSum(int[] nums, int target) {int n = nums.length;int left = 0;int right = n-1;while (left < right) {int sum = nums[left] + nums[right];if(sum == target) {return new int[]{left+1, right+1};}if(sum < target) {left++;}if(sum > target) {right--;}}return new int[]{-1, -1};}
}效果
1ms
99.36%
小结
这类题目的思路基本都是类似的。
我们有常见的几种解法:
1) 暴力
2)借助 Hash
3) 排序+二分
4)双指针==》针对有序数组
我们后续将看一下 n 数之和的系列,感兴趣的小伙伴点点赞,关注不迷路。
相关文章:

力扣.167 两数之和 II two-sum-ii
数组系列 力扣数据结构之数组-00-概览 力扣.53 最大子数组和 maximum-subarray 力扣.128 最长连续序列 longest-consecutive-sequence 力扣.1 两数之和 N 种解法 two-sum 力扣.167 两数之和 II two-sum-ii 力扣.170 两数之和 III two-sum-iii 力扣.653 两数之和 IV two-…...

ipconfig
本文内容来自智谱清言的回答。 ------ 以太网适配器 以太网: 媒体状态 . . . . . . . . . . . . : 媒体已断开连接 连接特定的 DNS 后缀 . . . . . . . : 以太网适配器 以太网: 这部分表示正在显示名为“以太网”的网络适配器的信息。在 Windows 中,默认的以太…...

Qt_day3_信号槽
目录 信号槽 1. 概念 2. 函数原型 3. 连接方式 3.1 自带信号 → 自带槽 3.2 自带信号 → 自定义槽 3.3 自定义信号 4. 信号槽传参 5. 对应关系 5.1 一对多 5.2 多对一 信号槽 1. 概念 之前的程序界面只能看,不能交互,信号槽可以让界面进行人机…...

求从2开始的第n个素数
方法一:暴力法 思路:从2开始,逐个判断每个数是否为素数。素数是除了1和它自身外,不能被其他自然数整除的数。对于每个数m,从2到sqrt(m)遍历,如果能被整除则不是素数。当找到n个素数时停止。 C 代码如下&am…...

【Android】View—基础知识,滑动,弹性滑动
基础知识 什么是View 在 Android 中,View 是用户界面(UI)中的基本组件,用于绘制图形和处理用户交互。所有的 UI 组件(如按钮、文本框、图片等)都是 View 的子类。可以说,View 是构建 Android …...

MYSQL中的两种转义操作
在 MySQL 中,转义字符用于处理特殊字符,以防止语法错误或 SQL 注入攻击,而单双引号都是需要重点注意的字符 可以用转义符\ 和 两个连续的引号 来起到转义引号的作用 转义符转义: 这是users表中的数据 如果查询admin 或者 admin" 用户,可以用转义符\ 两个连…...
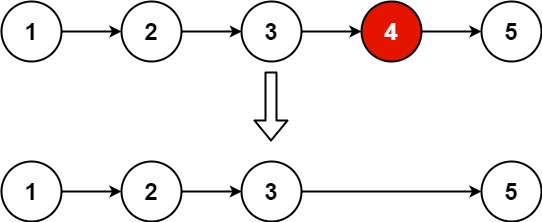
力扣题目解析--删除链表的倒数第n个节点
题目 给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。 示例 1: 输入:head [1,2,3,4,5], n 2 输出:[1,2,3,5]示例 2: 输入:head [1], n 1 输出:[]示例 3&…...
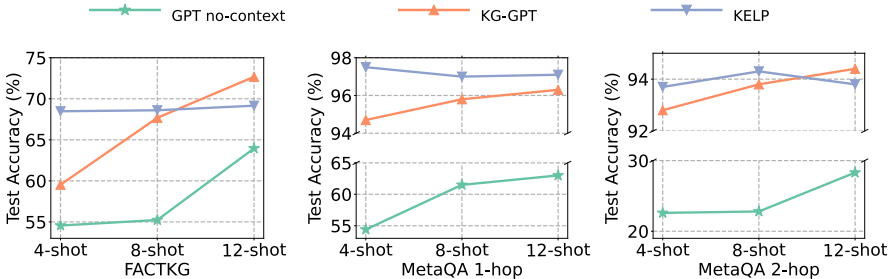
Knowledge Graph-Enhanced Large Language Models via Path Selection
研究背景 研究问题:这篇文章要解决的问题是大型语言模型(LLMs)在生成输出时存在的事实不准确性,即所谓的幻觉问题。尽管LLMs在各种实际应用中表现出色,但当遇到超出训练语料库范围的新知识时,它们通常会生…...

Android 项目模型配置管理
Android 项目配置管理 项目模型相关的配置管理config.gradle文件:build.gradle文件: 参考地址 项目模型相关的配置管理 以下是一个完整的build.gradle和config.gradle示例: config.gradle文件: ext {// 模型相关配置࿰…...

「QT」几何数据类 之 QSizeF 浮点型尺寸类
✨博客主页何曾参静谧的博客📌文章专栏「QT」QT5程序设计📚全部专栏「VS」Visual Studio「C/C」C/C程序设计「UG/NX」BlockUI集合「Win」Windows程序设计「DSA」数据结构与算法「UG/NX」NX二次开发「QT」QT5程序设计「File」数据文件格式「PK」Parasolid…...

Essential Cell Biology--Fifth Edition--Chapter one(2)
1.1.1.3 Living Cells Are Self-Replicating Collections of Catalysts 催化剂集合 生物最常被引用的特性之一是它们的繁殖能力。对于细胞来说,这个过程包括复制它们的遗传物质和其他成分,然后分裂成两个,产生一对子细胞[daughter cells]&a…...
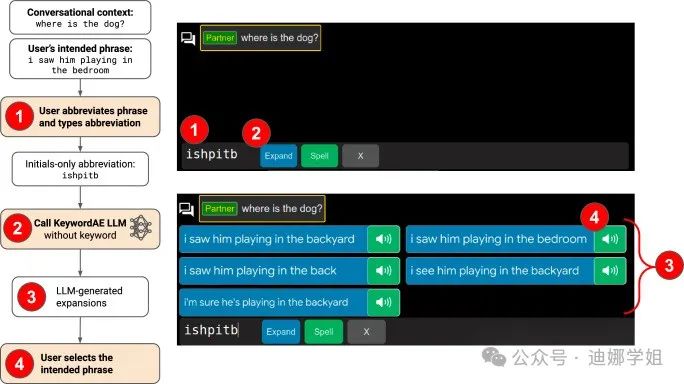
大语言模型LLMs在医学领域的最新进展总结
我是娜姐 迪娜学姐 ,一个SCI医学期刊编辑,探索用AI工具提效论文写作和发表。 相比其他学科,医学AI,是发表学术成果最多的领域。 医学数据的多样性和复杂性(包括文本、图像、基因组数据等),使得…...

云防护单节点2T抗攻击能力意味着什么?
随着互联网的发展,DDoS攻击的规模和频率不断增加,对企业和个人用户的网络服务造成了严重威胁。云防护服务作为一种高效的DDoS防护手段,逐渐成为许多企业的首选。本文将重点讨论云防护单节点2T(太比特每秒)抗攻击能力的…...

IDEA在编译时: java: 找不到符号符号: 变量 log
一、问题 IDEA在编译的时候报Error:(30, 17) java: 找不到符号符号: 变量 log Error:(30, 17) java: 找不到符号 符号: 变量 log 位置: 类 com.mokerson.rabbitmq.config.RabbitMqConfig 二、解决方案 背景:下载其他同事代码时,第一次运行,…...

HTML 基础架构:理解网页的骨架
HTML的文档结构主要由以下几个部分组成:<html>、<head>和<body>。 <html>标签是HTML文档的根元素,用来包裹整个HTML文档的内容。<head>标签用于定义文档的头部,包含了一些元数据和其他不直接显示在页面上的内…...

FPGA学习笔记#5 Vitis HLS For循环的优化(1)
本笔记使用的Vitis HLS版本为2022.2,在windows11下运行,仿真part为xcku15p_CIV-ffva1156-2LV-e,主要根据教程:跟Xilinx SAE 学HLS系列视频讲座-高亚军进行学习 从这一篇开始正式进入HLS对C代码的优化笔记 目录 1.循环优化中的基…...

web实操4——servlet体系结构
servlet体系结构 我们基本都只实现service方法,其余几个都不用, 之前我们直接实现servlet接口,所有的方法都必须实现,不用也得写,不然报错,写了又不用当摆设。 能不能只要定义一个service方法就可以&…...

Linux开发讲课48--- Linux 文件系统概览
本文旨在高屋建瓴地来讨论 Linux 文件系统概念,而不是对某种特定的文件系统,比如 EXT4 是如何工作的进行具体的描述。另外,本文也不是一个文件系统命令的教程。 每台通用计算机都需要将各种数据存储在硬盘驱动器(HDD)…...

Node.js 模块详解
模块的概念 Node.js 运行在 V8 JavaScript 引擎上,通过 require() 函数导入相关模块来处理服务器端的各种进程。一个 Node.js 模块可以是一个函数库、类集合或其他可重用的代码,通常存储在一个或多个 .js 文件中。 例如,启动一个 Node.js 服…...

大厂面试真题-说说tomcat的优缺点
Tomcat作为服务器,特别是作为Java Web服务器,具有一系列优点和缺点。以下是对其优缺点的详细分析: 优点 开源免费: Tomcat是一个免费、开源的Web服务器,用户可以在任何环境下自由使用,无需支付任何费用。…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...
