麦当劳自助点餐机——实现

餐厅自助点餐优点
1. 降低服务成本:
- 减少了对服务员数量的需求,降低了人力成本。
- 减轻了服务员的工作负担,使其能够更专注于提供优质的服务,如解决顾客的特殊需求和处理复杂问题。
2. 提升点餐效率和准确性:
- 避免了因服务员与顾客沟通不畅或误解导致的点餐错误。
- 顾客可以根据自己的节奏和喜好进行点餐,无需等待服务员的响应。
3. 优化顾客体验:
- 解决了因网络或手机卡顿导致的点餐不畅问题,让点餐过程更加流畅和便捷。
- 给予顾客更多的自主选择权利,满足个性化需求。
4. 便于管理和数据统计:
- 系统能够自动记录点餐数据,为餐厅的经营分析提供准确依据。
- 有助于优化菜品搭配和库存管理。
5. 提供小票打印:
- 为顾客提供清晰的消费明细,增加透明度和信任感。
- 方便顾客核对菜品和价格,减少纠纷。
Advantages of self-ordering in restaurants
1. Reduce service costs:
- Reduces the demand for the number of waiters, lowering labor costs.
- Reduces the workload of waiters, enabling them to focus more on providing high-quality services, such as addressing customers' special needs and handling complex issues.
2. Improve ordering efficiency and accuracy:
- Avoids ordering errors caused by poor communication or misunderstandings between waiters and customers.
- Customers can order according to their own pace and preferences without waiting for the response of waiters.
3. Optimize customer experience:
- Solves the problem of poor ordering caused by network or mobile phone lag, making the ordering process more smooth and convenient.
- Gives customers more autonomy and meets personalized needs.
4. Facilitate management and data statistics:
- The system can automatically record ordering data, providing an accurate basis for the restaurant's operation analysis.
- Helps optimize dish combinations and inventory management.
5. Provide receipt printing:
- Provides customers with a clear consumption detail, increasing transparency and trust.
- Facilitates customers to check dishes and prices, reducing disputes.
功能建造
自助机平台


普通公司制造,开发安卓设备软件,对接开放sdk即可
或者通过未来之窗开发平台直接使用
相关文章:

麦当劳自助点餐机——实现
餐厅自助点餐优点 1. 降低服务成本: - 减少了对服务员数量的需求,降低了人力成本。 - 减轻了服务员的工作负担,使其能够更专注于提供优质的服务,如解决顾客的特殊需求和处理复杂问题。 2. 提升点餐效率和准确性…...

C++ STL CookBook 6:STL Containers (I)
目录 顺序容器 关联容器 容器适配器 使用统一擦除函数从容器中删除指定项 在恒定时间内对一个对排序不敏感的vector中删除项目 如果不确定自己访问容器会不会越界,那就使用.at方法而不是[] 在我们开始之前,先来回顾一下传统的经典的几个容器&#…...

行转列实现方式总结
前言 在日常开发中遇到了,需要对表中数据某个字段行数据转成列,个人觉得这中做目前想到两种, 一种是sql 操作, 另一种代码中做逻辑处理。 方式一 Java 操作 import lombok.Data;import java.util.ArrayList; import java.util.H…...

【go从零单排】初探goroutine
🌈Don’t worry , just coding! 内耗与overthinking只会削弱你的精力,虚度你的光阴,每天迈出一小步,回头时发现已经走了很远。 📗概念 Goroutines 是 Go 语言中的一种轻量级线程,用于并发编程。它们允许程…...

HarmonyOS NEXT应用元服务开发Intents Kit(意图框架服务)本地搜索接入方案
一、方案概述 当用户使用应用/元服务时,开发者可以按照标准意图Schema向系统共享数据,并支持意图调用(空调用与传参调用),以实现用户点击卡片后,可后台执行功能(例如播放指定歌曲)或…...

C语言可变参数列表编程实战指南:从基础概念到高级应用的全面解析
引言 在C语言中,可变参数列表的功能使得函数能够灵活地处理不确定数量的输入参数。本文将深入探讨可变参数列表的基础概念、技术原理及其在实际编程中的应用,帮助开发者更好地理解和使用这一特性。 一、可变参数列表的基本概念 1.1 什么是可变参数列表…...

AndroidStudio-文本显示
一、设置文本的内容 1.方式: (1)在XML文件中通过属性:android:text设置文本 例如: <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas.andr…...
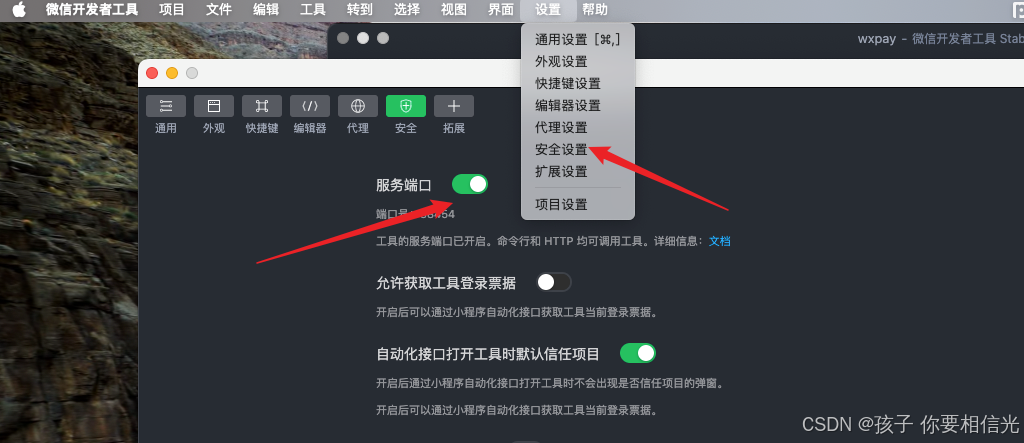
HBuilderX运行微信小程序,编译的文件在哪,怎么运行
1. 点击HBuilderX顶部的运行-运行到小程序模拟器-微信开发者工具,就会开始编译 2. 编译完成后的文件在根目录找到 unpackage -- dist -- dev -- mp-weixin, 这里面就是编译后的文件,如果未跳转到开发者工具,那可能是没设置启动路径࿰…...

百亿AI数字人社会初现:Project Sid展示智能代理文明进化路径
项目背景 Project Sid 是一项开创性的AI代理人文明实验,旨在通过新开发的认知架构 PIANO 探讨AI代理人是否能够在大规模数字社会中实现文明的演进。这项实验不仅展示了社会进步、角色分化、治理体系及文化传播等特征,还揭示了一个包含百亿“数字人类”的社会可能性。 PIANO…...

代码随想录训练营Day21 | 491.递增子序列 - 46.全排列 - 47.全排列 II - 332.重新安排行程 - 51.N皇后 - 37.解数独
491.递增子序列 题目链接:491.递增子序列思路:和子集那道题思路很像,每次在数组中选择一个数,选过的数不能选择,这里要求集合数量必须大于2个才能符合,仍然需要去重,但这里选额的是子序列&…...

多用户商城系统的功能及设计和开发
多用户商城系统的功能及设计与开发(基于 PHP MySQL) 在现代电子商务平台的开发中,PHP MySQL 是一对非常流行且高效的技术栈。PHP作为服务器端脚本语言,结合MySQL数据库,可以高效地处理多用户商城系统的各种需求。本…...

2024年11月8日day8
半加器和全加器的区别 半加器:只能处理两个二进制位的相加,无法处理进位。全加器:不仅能处理两个二进制位的相加,还能处理来自低位的进位。 ⑴ 完成满足754标准存储格式的浮点数((43940000)16的十进制数值)…...

Debezium系列之:Debezium3版本增量快照和只读增量快照应用的变化
Debezium系列之:Debezium3版本增量快照和只读增量快照应用的变化 一、需求背景二、基于数据库信号表使用增量快照案例三、基于Kafka信号Topic使用增量快照案例四、只读增量快照案例五、增量快照技术总结增量快照相关知识请阅读博主下面系列文章: Debezium系列之:实现增量快照…...

Python正则表达式1 re.match惰性匹配详解案例
点个关注 re.match() re.match() 函数尝试从字符串的开头开始匹配一个模式,如果匹配成功,返回一个匹配成功的对象,否则返回None。大小写区分,内容匹配不到后面的,只能匹配一个,不能有空格(开头匹配&#…...
学习日志10:Prism框架下按键绑定)
WPF(C#)学习日志10:Prism框架下按键绑定
在Prism框架下,提供了DelegateCommand类用于处理了UI的按键请求,XAML中可以直接采用 Command"{Binding **}" 来绑定这些方法。这个类是一个泛型的类生命时仅需要DelegateCommand<T>即可,同时在XAML中绑定CommandParameter&qu…...

WPF中的ResizeMode
在 WPF (Windows Presentation Foundation) 中,ResizeMode 属性用于指定窗口是否可以被用户调整大小,以及如何调整大小。ResizeMode 属性可以设置为以下几个值之一: NoResize:窗口不能被用户调整大小,但可以被程序代码…...

Unity3D UI 双击和长按
Unity3D 实现 UI 元素双击和长按功能。 UI 双击和长按 上一篇文章实现了拖拽接口,这篇文章来实现 UI 的双击和长按。 双击 创建脚本 UIDoubleClick.cs,创建一个 Image,并把脚本挂载到它身上。 在脚本中,继承 IPointerClickHa…...
LabVIEW扫描探针显微镜系统
开发了一套基于LabVIEW软件开发的扫描探针显微镜系统。该系统专为微观尺度材料的热性能测量而设计,特别适用于纳米材料如石墨烯、碳纳米管等的研究。系统通过LabVIEW编程实现高精度的表面形貌和热性能测量,广泛应用于科研和工业领域。 项目背景 随着纳…...

问题式教学法在生物教学中的应用探索
问题式教学法在生物教学中的应用探索 李新 山东省德州市平原县第五中学 山东 德州 253100 摘要:时代在发展教育事业也在不断进步,不断创新教学方法有利于提高教学质量。问题教学法能让教材知识点以问题的形式呈现在学生眼前,这对引导学生…...

C++ | Leetcode C++题解之第556题下一个更大元素III
题目: 题解: class Solution { public:int nextGreaterElement(int n) {int x n, cnt 1;for (; x > 10 && x / 10 % 10 > x % 10; x / 10) {cnt;}x / 10;if (x 0) {return -1;}int targetDigit x % 10;int x2 n, cnt2 0;for (; x2 …...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...
