【算法】【优选算法】二分查找算法(上)
目录
- 一、二分查找简介
- 1.1 朴素二分模板
- 1.2 查找区间左端点模版
- 1.3 查找区间右端点模版
- 二、leetcode 704.⼆分查找
- 2.1 二分查找
- 2.2 暴力枚举
- 三、Leetcode 34.在排序数组中查找元素的第⼀个和最后⼀个位置
- 3.1 二分查找
- 3.2 暴力枚举
- 四、35.搜索插⼊位置
- 4.1 二分查找
- 4.2 暴力枚举
- 五、69.x的平⽅根
- 4.1 二分查找
- 4.2 暴力枚举

一、二分查找简介
运用场景:
- 当数组是有二段性的时候就可以使用,
- 二段性就是指:我们可以找到一个相同规律每次都能够选取一个数,将当前数组分成两段。
- 我们计算中点的时候有两种计算方法,mid = (right + left) / 2 = left + (right - left) / 2 和 mid = (right + left +1) / 2 = left + (right - left +1)。
-
- 这两种方式对于奇数长度的数组来说,没区别,但是对于偶数长度来说,中点有两个点(比如长度为四的数组,中点就可以是1下标也可以是2下标),第一个就是拿到前一个中点,第二个就是拿到后一个中点。
1.1 朴素二分模板
模版:
while(left <= right) {int mid = left + (right - left) / 2;if(……) left = mid + 1;else if(……) right = mid - 1;else return ……;
}
1.2 查找区间左端点模版
模版:
while(left < right) {int mid = left + (right - left) / 2;if(……) left = mid + 1;else right = mid;
}
1.3 查找区间右端点模版
模版:
while(left < right) {int mid = left + (right - left + 1) / 2;if(……) left = mid; else right = mid - 1;
}
这两个模版详解在目录三的3.1题解中,也就是Leetcode 34.在排序数组中查找元素的第⼀个和最后⼀个位置的题解。
细节理解
- 循环条件left <= right :这是因为,如果当前[left , right ]区间中只有一个元素的时候,我们还是需要进行比较。
- mid = left + ( right - left) / 2:这是因为,我们直接使用(left + right) / 2来求中间值,如果数组很大那么left + right的值是可能超过int的范围的,减法就没有这种风险。
二、leetcode 704.⼆分查找
题目链接:leetcode 704.⼆分查找
题目描述:

题目解析:
- 这道题就是在一个有序数组中找到一个等于目标值的元素的下标,没找到就返回-1。
2.1 二分查找
解题思路:
- 直接套用上面的朴素模版即可。
解题代码:
//时间复杂度:O(logN)
//空间复杂度:O(1)
class Solution {public int search(int[] nums, int target) {int left = 0;int right = nums.length-1;while(left <= right) {int mid = left + (right-left) / 2;if(nums[mid] == target) return mid;else if(nums[mid] < target) left = mid + 1;else right = mid - 1;}return -1;}
}
2.2 暴力枚举
解题思路:
- 直接遍历数组,让目标值与每一个元素相比较,如果相等,那么就返回当前下标。
- 数组遍历完,没找到相等元素,返回-1即可。
解题代码:
//时间复杂度:O(n)
//空间复杂度:O(1)
class Solution {public int search(int[] nums, int target) {for(int i = 0; i < nums.length; i++) {if(nums[i] == target) return i;}return -1;}
}
三、Leetcode 34.在排序数组中查找元素的第⼀个和最后⼀个位置
题目链接:Leetcode 34.在排序数组中查找元素的第⼀个和最后⼀个位置
题目描述:

题目解析:
- 给的是一个非递减数组,意思就是这个数组中元素的值是一定大于或等于前面一个元素的。
- 返回数组中等于target的子数组的头尾下标,如果只有一个,那么该下标即是头也是尾,如果没有返回两个-1。
- 题目要求使用复杂度为O(logN),但是其实O(N^2)和O(N)也能过。
3.1 二分查找
解题思路:
- 当我们要找的是一段区间,那么我们可以尝试分别去找左端点和右端点,这样就是一个区间了。
- 我们将数组拆分,可以以等于target来拆分,
-
- 分法一:一段是 >= target的元素,一段是 < target元素,这就是求左端点的分法。
-
- 分法二:一段是 <= target的元素,一段是 > target元素,这就是求右端点的分法。
- 上面两种分法,都是不断按照同一个规律,将数组拆分为两段,这就是二段性的体现。
- 求左端点:
-
- 循环条件:left < right 因为我们是求的左端点,其中并不会写返回语句,当我们left和right相等的时候,我们如果还进循环,就会陷入死循环,并且其实这个时候就是我们要求的左端点了。
-
- 中点的求法:mid = left + (right - left) / 2; 因为当我们只有两个节点时,求取到后一个节点作为中点时,就让mid指向right了,后续更新mid还会指向这里,陷入死循环。
-
- 当mid元素 >= target的时候,因为我们求的是左端点,当前的左端点肯定在[ left , mid]区间之间,并且有可能就是mid,所以要让right指向mid。
-
- 当mid元素 < target 的时候,左端点肯定在( mid , right ] 区间,所有让 left = mid + 1;
- 求右端点:
-
- 循环条件:left < right 因为我们是求的右端点,其中并不会写返回语句,当我们left和right相等的时候,我们如果还进循环,就会陷入死循环,并且其实这个时候就是我们要求的右端点了。
-
- 中点的求法:mid = left + (right - left + 1) / 2; 因为当我们只有两个节点时,以第一个节点为中点,求取到后面就让mid指向left了,后续更新mid还会指向这里,又陷入死循环。
-
- 当mid元素 <= target的时候,因为我们求的是右端点,当前的右端点肯定在[ mid, right ]区间之间,并且有可能就是mid,所以要让left指向mid。
-
- 当mid元素 > target 的时候,右端点肯定在[ left, mid ) 区间,所有让 right = mid - 1;
- 在左右端点求取之间,我们还要更新一下结果中的端点值,如果没找到端点,那么就代表给返回[-1, -1]了。
- 边界:当数组中没有元素的时候,我们去求端点的时候是会直接越界的,所以这种情况要单独处理。
解题代码:
//时间复杂度:O(logN)
//空间复杂度:O(1)
class Solution {public int[] searchRange(int[] nums, int target) {int[] ret = new int[]{-1,-1};//边界if(nums.length == 0) return ret;//查找左端点int left = 0;int right = nums.length-1;while(left < right) {int mid = left + (right-left)/2;if(nums[mid] < target) left = mid + 1;else right = mid;}if(nums[left] == target) ret[0] = left; else return ret;//查找右端点right = nums.length-1;while(left < right) {int mid = left + (right-left+1)/2;if(nums[mid] > target) right = mid -1;else left = mid;}ret[1] = left;return ret;}
}
3.2 暴力枚举
解题思路:
- 我们直接一个for循环,遍历数组,当遇到等于目标值的时候,再一层for循环遍历区间尾即可。
解题代码:
//时间复杂度:O(n^2)
//空间复杂度:O(1)
class Solution {public int[] searchRange(int[] nums, int target) {int[] ret = new int[]{-1,-1};for(int i = 0; i < nums.length; i++) {if(nums[i] == target) {ret[0] = i;for(int j = i; j < nums.length ;j++) {if(j+1 >= nums.length || nums[j+1] > target) {ret[1] = j;return ret;}}}}return ret;}
}
优化:
- 我们可以借助滑动窗口的思想,
- 当我们遇到等于目标值的元素之后,并且left还是初始值的时候,我们就可以将ret[ 0 ]更新。
- 每次right遇到等于目标值的元素的时候,就更新ret[ 1 ]。
//时间复杂度:O(n)
//空间复杂度:O(1)
class Solution {public int[] searchRange(int[] nums, int target) {int[] ret = new int[]{-1,-1};for(int left = -1,right = 0; right < nums.length; right++) {if(nums[right] == target) {ret[1] = right;if(left == -1) {left = right;ret[0] = right;}}if(nums[right] > target) break;}return ret;}
}
四、35.搜索插⼊位置
题目链接:35.搜索插⼊位置
题目描述:

题目解析:
- 数组是升序的,当数组中有等于target,返回该元素下标。
- 如果没有,返回比他小的最近元素的下一个下标。
4.1 二分查找
解题思路:
- 套用上面求左右端点的模版都可以求。
- 有一种边界情况没有求,也就是示例3的情况。单独考虑。
解题代码:
//时间复杂度:O(logN)
//空间复杂度:O(1)
class Solution {public int searchInsert(int[] nums, int target) {int left = 0;int right = nums.length - 1;while(left < right) {int mid = left + (right - left ) / 2;if(nums[mid] < target) left = mid + 1;else right = mid;}if(nums[right] >= target) return right;return right+1;}
}class Solution {public int searchInsert(int[] nums, int target) {int left = 0;int right = nums.length - 1;while(left < right) {int mid = left + (right - left + 1) / 2;if(nums[mid] > target) right = mid - 1;else left = mid;}if(nums[right] >= target) return right;return right+1;}
}
4.2 暴力枚举
解题思路:
- 直接遍历数组。
- 处理边界情况,插入0位置或者插入数组尾。
解题代码:
//时间复杂度:O(n)
//空间复杂度:O(1)
class Solution {public int searchInsert(int[] nums, int target) {for(int i = 0; i < nums.length; i++) {if(nums[i] == target) return i;if(nums[i] < target && i < nums.length - 1 && nums[i+1] > target) return i+1;} if(nums[0] >= target) return 0; return nums.length;}
}
五、69.x的平⽅根
题目链接:69.x的平⽅根
题目描述:

题目解析:
- 求一个数的算术平方根,向下取整。
4.1 二分查找
解题思路:
- 我们可以将 1 - x 的数分为两个区间:小于x算术平方根的区间,大于等于算术平方根的区间。
- 因为我们需要求的是小于等于算术平方根的最大值,所以相当于求右端点。
- 套用模版,处理一下边界情况即可。
- 因为这道题的x范围是整个int,所以当我们求平方的时候是可能超出int范围的,所以我们使用long。
解题代码:
//时间复杂度:O(logN)
//空间复杂度:O(1)
class Solution {public int mySqrt(int x) {long left = 1;long right = x;//边界情况if(x <= 1) return x;while(left < right) {long mid = left + (right - left + 1) / 2;if(mid * mid <= x) left = mid;else right = mid - 1;}return (int)left;}
}
4.2 暴力枚举
解题思路:直接使用一个for循环,将0 到x 的数遍历,看是否符合要求即可。
解题代码:
//时间复杂度:O(n)
//空间复杂度:O(1)
class Solution {public int mySqrt(int x) {for(long i = 0; i <= x; i++) {if(i * i == x) return (int)i;else if(i * i < x && (i+1) * (i+1) > x) return (int)i;}return 0;}
}
相关文章:

【算法】【优选算法】二分查找算法(上)
目录 一、二分查找简介1.1 朴素二分模板1.2 查找区间左端点模版1.3 查找区间右端点模版 二、leetcode 704.⼆分查找2.1 二分查找2.2 暴力枚举 三、Leetcode 34.在排序数组中查找元素的第⼀个和最后⼀个位置3.1 二分查找3.2 暴力枚举 四、35.搜索插⼊位置4.1 二分查找4.2 暴力枚…...

springboot初体验
目录 环境 controller 修改端口号 更改banner图标 运行结果 最核心的:自动装配 环境 jdk17springboot3.3.5maven3.8.2 controller controller层和启动类同级 package com.example.demo.controller; import org.springframework.web.bind.annotation.RequestMapping;…...
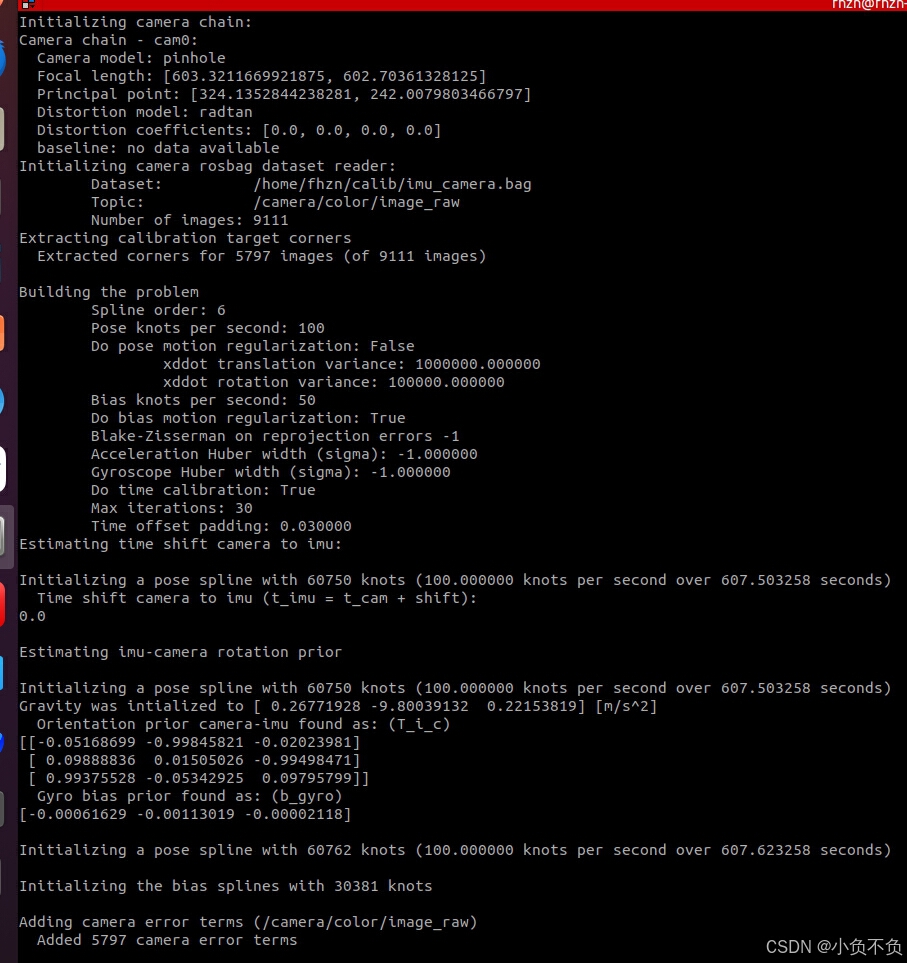
使用kalibr_calibration标定相机(realsense)和imu(h7min)
vslam-evaluation/VINS/Installation documentation/4.IMU和相机联合标定kalibr_calibration.md at master DroidAITech/vslam-evaluation GitHub 目录 1.kalibr安装 1.1安装依赖项 1.2创建工作空间 1.3下载kalibr并编译 1.4设置环境变量 2.准备标定板 3.配置驱动和打…...

绿色工厂认定流程
以下是认定绿色工厂的一般流程: 编制年度创建计划 各省辖市、省直管县(市)会结合本地区重点产业发展现状,挑选一批基础条件良好、有创建意愿和条件的企业进行储备培育,并依据当地工业企业发展实际情况按年度制定绿色工…...

《Python游戏编程入门》注-第5章5
《Python游戏编程入门》的“Analog Clock示例程序”部分讲解了模拟时钟的实现方法。该模拟时钟可以通过时针、分针和秒针的旋转,显示当前时间,如图1所示。 图1 模拟时钟 1 绘制圆 从图1中可以看出,时钟的边缘是一个白色的圆,可以通过如图2所示的代码进行绘制。 图2 绘制圆…...

LangChain Ollama实战文献检索助手(二)少样本提示FewShotPromptTemplate示例选择器
本期是用样例来提示大模型生成我们想要的答案。即在输入中给定提示的样例,以及提示模板,然后匹配较相关的样例进行文献综述。 创建示例样本FewShotPromptTemplate 这里我用GTP-o1生成了几个回答,作为样本 samples [{"theme": &…...

K倍区间 C++
1230. K倍区间 - AcWing题库 一开始想到的用前缀和来做,时间复杂度为O(n^2),Time Limit Exceeded #include <iostream> #include <cstring> #include <algorithm> #include <cstdio>using namespace std;const int N 100010;int n,k; in…...

Linux - 弯路系列3:安装和编译libvirt-4.5.0
系统:Anolis8(离线) 目录 1、步骤2、make过程中的错误错误1:error: xdr_u_int64_t undeclared (first use in this function) 3、make install的错误错误1:/usr/bin/mkdir -p ""/usr/local/etc/libvirt/nwf…...

Jenkins插件使用问题总结
Git Push插件 插件介绍 主要是用于git推送代码到远程仓库中使用,插件地址 pipeline中使用 官方说明中只有一句代码gitPush(gitScm: scm, targetBranch: env.BRANCH_NAME, targetRepo: origin) 流水线语法中也做的不齐全所以一开始我老是设置错,导致代…...
u盘怎么重装电脑系统_u盘重装电脑系统步骤和详细教程【新手宝典】
u盘怎么重装电脑系统?一个u盘怎么重装电脑系统呢,需要将u盘制作成u盘启动盘pe,然后通过U盘启动盘进入pe进行安装系统,下面小编就教大家u盘重装电脑系统步骤和详细教程。 u盘启动是什么意思? U盘启动盘是一种具有特殊功…...

Sql server查询数据库表的数量
SELECT count(*) FROM sys.objects WHERE typeU --统计表数量 SELECT NAME FROM sys.objects WHERE typeU --列出表名称 或者 SELECT COUNT(*) FROM SysObjects Where XTypeU --统计表数量 SELECT Name FROM SysObjects Where XTypeU --列出表名称 --判断字…...

Linux学习笔记之软件包管理RPM与YUM
RPM包的管理 介绍 RPM(RedHat Package Manager)用于互联网下载包的打包及安装工具,它包含在某些Linux分发版中。他生成具有.RPM扩展名的文件。RPM类似Windows的setup.exe,这一文件格式虽然打上了RedHat的标志,但理念…...

15分钟学 Go 第 41 天:中间件的使用
第41天:中间件的使用 目标:学习如何在Go语言的Web服务中使用中间件 中间件(Middleware)是Web开发中的一种常见设计模式,通常用于处理请求和响应过程中的一些共通功能。比如:日志记录、认证授权、请求处理…...

《Python 与 SQLite:强大的数据库组合》
《Python 与 SQLite:强大的数据库组合》 一、Python 与 SQLite 的结合二、安装与连接(一)安装 SQLite 模块(二)连接到数据库 三、数据库操作(一)创建表格(二)插入数据&am…...

Golang | Leetcode Golang题解之第552题学生出勤记录II
题目: 题解: const mod int 1e9 7type matrix [6][6]intfunc (a matrix) mul(b matrix) matrix {c : matrix{}for i, row : range a {for j : range b[0] {for k, v : range row {c[i][j] (c[i][j] v*b[k][j]) % mod}}}return c }func (a matrix) p…...

Vue3 常用代码指南手抄,超详细 cheatsheet
一、Vue3 基础 1.1 创建 Vue3 项目 使用 Vite 创建 npm create vitelatest my-vue-app -- --template vue cd my-vue-app npm install npm run dev使用 Vue CLI 创建 npm install -g vue/cli vue create my-vue-app1.2 项目结构 my-vue-app ├── node_modules ├── pu…...

结构体是否包含特定类型的成员变量
结构体是否包含特定类型的成员变量 在C中,可以使用模板元编程和类型特性(type traits)来判断一个结构体是否包含特定类型的成员变量。这通常通过std::is_member_object_pointer类型特性来实现,它可以用来检查给定的成员指针是否指…...

堆排序与链式二叉树:数据结构与排序算法的双重探索
大家好,我是小卡皮巴拉 文章目录 目录 引言 一.堆排序 1.1 版本一 核心概念 堆排序过程 1.2 版本二 堆排序函数 HeapSort 向下调整算法 AdjustDown 向上调整算法 AdjustUp 二.链式二叉树 2.1 前中后序遍历 链式二叉树的结构 创建链式二叉树 前序遍历…...
用 Python 从零开始创建神经网络(四):激活函数(Activation Functions)
激活函数(Activation Functions) 引言1. 激活函数的种类a. 阶跃激活功能b. 线性激活函数c. Sigmoid激活函数d. ReLU 激活函数e. more 2. 为什么使用激活函数3. 隐藏层的线性激活4. 一对神经元的 ReLU 激活5. 在隐蔽层中激活 ReLU6. ReLU 激活函数代码7. …...
使用 Flask 和 ONLYOFFICE 实现文档在线编辑功能
提示:CSDN 博主测评ONLYOFFICE 文章目录 引言技术栈环境准备安装 ONLYOFFICE 文档服务器获取 API 密钥安装 Flask 和 Requests 创建 Flask 应用项目结构编写 app.py创建模板 templates/index.html 运行应用功能详解文档上传生成编辑器 URL显示编辑器回调处理 安全性…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...
