解线性方程组(二)
实验类型:●验证性实验 ○综合性实验 ○设计性实验
实验目的:进一步熟练掌握用Jacobi迭代法和Gauss-Seidel法解线性方程组的算法,提高编程能力和解算线性方程组问题的实践技能。
实验内容:
1)取初值性x(0)=(0,0,0,0)T, 精度要求ε=10-6,用Jacobi迭代法解线性方程组

2)取初值性x(0)=(0,0,0,0)T, 精度要求ε=10-6,用Gaoss-Seidel迭代法解线性方程组

实验原理:Jacobi迭代算法,Gaoss-Seidel迭代算法。
实验任务及说明:
- 从一般迭代法收敛性理论上分析并讨论1)、2)两个问题所选用的迭代方法是否收敛,若分析过程涉及到四次代数方程求根可用Matlab的roots函数求多项式的根,请将分析、讨论过程及收敛性结论写在规格为A4的打印纸上。
- 分别用Jacobi迭代算法,Gaoss-Seidel迭代算法手工解算1)、2)两个问题的线性方程组,清楚的写出迭代公式,要求严格按照算法步骤手工计算,其中间计算结果保留五位小数,手工迭代至少迭代三步,计算出X(1),X(2),X(3),请将手工计算过程写在规格为A4的打印纸上,对计算过程进行总结和梳理后在A4纸上分别手工画出Jacobi迭代算法,Gaoss-Seidel迭代算法的程序设计流程图(提示:算法开始或结束--用椭圆框;类似赋值语句(算法公式)的执行处理--用矩形框,赋值语句(算法公式)写在矩形框内;条件判断---用菱形框,条件判断表达式写在菱形框里,条件判断必须有两个出口即两个流出的流程线,在流出的流程线傍边要清楚的标出Yes或No)。
- 用Matlab编写程序上机计算并输出中间结果(可参考马昌凤柯艺芬编著的数值计算方法(MATLAB版) ,科学出版社2020.11. Page49,Page51 );请将算法流程图(使用Word画图)、程序代码、调试截图记录、输入数据截图记录、输出的中间结果截图记录及最终计算的结果截图记录等作为实验报告内容编排成word文档,然在规格为A4的打印纸上双面打印,实验报告中的word文档的文字采用宋体5号,单倍行距,报告中截图上的文字不得小于宋体六号,截图文字的字迹必须清晰可见!。
- 请在实验报告中验证计算机程序迭代计算的前三步近似解向量X(1),X(2),X(3)与手工迭代计算的前三步近似解向量X(1),X(2),X(3)是否一致,要求将手工计算的前三步结果和计算机程序计算的前三步结果列表对比,经过对比分析在列表后的文档中清楚给出是否一致的验证结论。
- 纸质版实验报告装订顺序:①实验任务(本文档版式不得做任何改动);②实验报告正文(Word文档);③写在A4纸上的手工分析与计算(也可以将A4纸上详细手工分析与计算过程拍照成JPG图片插入在实验报告的word 电子版中随Word文档双面打印)。
实验步骤
- 要求上机实验前先进行算法收敛性分析并手工计算、对手工计算进行总结后画出流程图,再编写出程序代码;
- 编辑录入程序;
- 记录运行时的输入(截图)和输出(截图)。调试程序并记录调试过程中出现的问题(截图)及修改程序的过程(截图);
- 经反复调试后,运行程序并验证程序运行是否正确,必须明确写出分析对比过程及验证结论。
实验报告:根据实验情况和结果撰写并递交实验报告(含手工分析与计算)。
实验总结:(学会了......; 掌握了......; 训练了......; 发现了......; 今后学习中......有待提高。)
程序代码
电子报告word文件命名规则:专业班级-完整学号-实验X-姓名.doc, 如信息123班学号为201212030315的郭海涛同学实验2报告word文件命名则应是:信息123-201212030315-实验2-郭海涛.doc, 其中 .doc是Word文件扩展名。
特别提醒:学委负责检查电子文件命名规范,命名不规的将不接收。每人必需提交电子报告和纸质报告各一份(两者内容一致,纸质版实验报告要求用A4纸张双面打印,按规定的装订顺序装订)。本实验任务书版式不得做任何改动。电子报告以班为单位提交压缩包.
问题一:
手写算法迭代过程及判断是否收敛过程:

流程图:
算法流程图:

程序设计流程图:

程序代码:
function [y,n]=Jacobi(A,b,x0,ep)
A=[14 4 4 4;4 14 4 4;4 4 14 4;4 4 4 14];
b=[-4;16;36;56];
x0=[0;0;0;0];
% epslion为误差值
epslion=1.0000e-06;
% N为自己设置的迭代次数
N=100;
D=diag(diag(A)); %D为A的对角矩阵
U=triu(A,1); %U为A的上三角矩阵
B=-D\(L+U); %B为迭代矩阵
g=D\b;error=1;n=0;
for i=1:N
while error>epslion && n<N
y=x0;x0=B*x0+g;error=norm(y-x0,inf);
if error>epslion
n=n+1;
fprintf('第%d次jacobi迭代结果为:',n)
disp(x0);
fprintf('第%d次迭代结果的误差为:\n',n);disp(error)
break
end
if error<=epslion
n=n+1;fprintf('第%d次jacobi迭代结果为:',n)
disp(x0);fprintf('第%d次迭代结果的误差为:\n',n);disp(error);
fprintf('该方程组的jacobi迭代法的最小迭代次数为:')
disp(n);break
end
end
end
end

| 变量 | X1(k) | X2(k) | X3(k) | X4(k) | ||||
| 迭代次数 | 手算 | Matlab | 手算 | Matlab | 手算 | Matlab | 手算 | Matlab |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | -0.28571 | -0.2857 | 1.14286 | 1.1429 | 2.57143 | 2.5714 | 4.00000 | 4.0000 |
| 2 | -2.48980 | -2.4898 | -0.65306 | -0.6531 | 1.18367 | 1.1837 | 3.02041 | 3.0204 |
| 3 | -1.30029 | -1.3003 | 0.65306 | 0.6531 | 2.60641 | 2.6064 | 4.55977 | 4.5598 |
手工计算过程中保留五位小数,matlab程序中保留的是四位小数,将我手工计算的结果保留四位小数和matlab的结果比对后完全一致。
问题2:
程序代码:
function x=Gauss_Seidel_fun(A,b,n,x0,tol,N)
k=-1;
while k<N
for i=1:n
if i==1
x(1)=(b(1)-A(1,2:n)*x0(2:n))/A(1,1);
elseif i==n
x(n)=(b(n)-A(n,1:n-1)*x(1:n-1))/A(n,n);
else
x(i)=(b(i)-A(i,1:i-1)*x(1:i-1)-A(i,i+1:n)*x0(i+1:n))/A(i,i);
end
end
if norm(x-x0)<tol
break;
end
x0=x;k=k+1;
disp(['when k=',num2str(k)]);
disp('x=');disp(x); %输出中间结果
end
if k==N
disp('迭代次数已到达上限!');
end
disp(['迭代次数 k=',num2str(k)])
end
运行时的输入和输出:

手工计算结果与程序运行结果对比:
| 变量 | X1(k) | X2(k) | X3(k) | X4(k) | ||||
| 迭代次数 | 手算 | Matlab | 手算 | Matlab | 手算 | Matlab | 手算 | Matlab |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | -2.66667 | -2.6667 | 0.05556 | 0.0556 | 0.89815 | 0.8981 | 4.35725 | 4.3573 |
| 2 | -1.77225 | -1.7722 | 0.64258 | 0.6426 | 2.59747 | 2.5975 | 4.62232 | 4.6223 |
| 3 | -1.35627 | -1.2492 | 0.87560 | 0.8935 | 2.79399 | 2.8725 | 4.69278 | 4.7248 |
手工计算过程中保留五位小数,matlab程序中保留的是四位小数,将我手工计算的结果保留四位小数和matlab的结果比对后在k=0和k=1时完全一致,在k=3时有出入。
实验总结:
学会了另外两种迭代方法:Jacobi迭代法和Gauss-Seidel法求解线性方程组,以及如何判断算法收敛; 掌握了这两种迭代方法的求解迭代过程以及word画流程图,还有这两种算法在面对同一个线性方程组的优势; 训练了function函数的使用以及在纸上解题的能力和独立思考以及自学能力,还有独立编程并实现这两种算法的能力; 今后学习中对于算法框图的构建以及程序设计框图的展现还有待提高。
相关文章:

解线性方程组(二)
实验类型:●验证性实验 ○综合性实验 ○设计性实验 实验目的:进一步熟练掌握用Jacobi迭代法和Gauss-Seidel法解线性方程组的算法,提高编程能力和解算线性方程组问题的实践技能。 实验内容: 1)取初值性x(0)(0,0,0,0)T, 精度要求ε…...
HarmonyOS Next 实战卡片开发 02
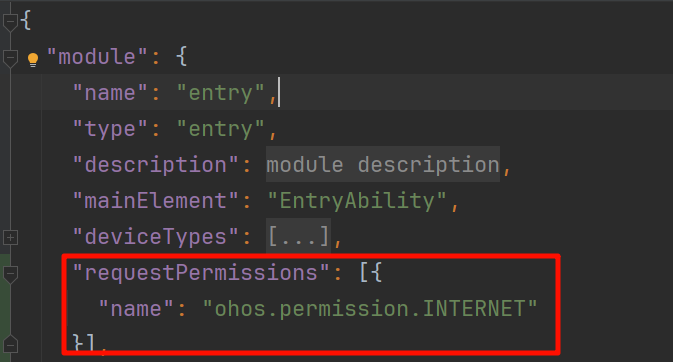
HarmonyOS Next 实战卡片开发 02 卡片开发中,还有一个难点是显示图片。其中分为显示本地图片和显示网络图片 显示本地图片 卡片可以显示本地图片,如存放在应用临时目录下的图片。路径比如 /data/app/el2/100/base/你的项目boundleName/temp/123.png 以…...

FastDDS服务发现之PDP的收发
目录 PDP发送PDP接收EDP更新 EntityID 通过FastDDS服务发现之PDP和EDP的创建这一节内容,可以了解服务发现的概念,机制和PDP/EDP中各类对象的创建,本文详细介绍Simple PDP发送数据,接收数据和处理报文的流程。 PDP发送 通过在RTP…...
)
【计网不挂科】计算机网络期末考试——【选择题&填空题&判断题&简述题】试卷(2)
前言 大家好吖,欢迎来到 YY 滴计算机网络 系列 ,热烈欢迎! 本章主要内容面向接触过C的老铁 本博客主要内容,收纳了一部门基本的计算机网络题目,供yy应对期中考试复习。大家可以参考 本章是去答案版本。带答案的版本在下…...
)
关于有机聚合物铝电容的使用(2)
在使用时需要特别注意的几个应用场景: 在有较长供电电缆或PCB电源布线较长的场合。 这个场景应当仍与有机聚合物铝电容的耐压有关。 假设在相同的冲击电流下,较长的供电电缆和PCB布线,那么电缆和PCB布线上产生的冲击电压就会越高。故而&…...

Linux -- 进程初印象
目录 预备知识 切入点 PCB 看见进程 pid getpid 函数 预备知识 Linux -- 冯诺依曼体系结构(硬件)-CSDN博客https://blog.csdn.net/2301_76973016/article/details/143598784?spm1001.2014.3001.5501 Linux -- 操作系统(软件…...

【超级简单】Facebook脸书视频下载一键保存手机
Facebook作为目前服务全球30亿用户,尤其是出海和跨境用户没有办法忽视的平台,提供了一个在线平台,使用户分享照片、视频、状态更新和链接等内容,然而,令人遗憾的是,用户没有办法直接将照片和视频保存到本地…...
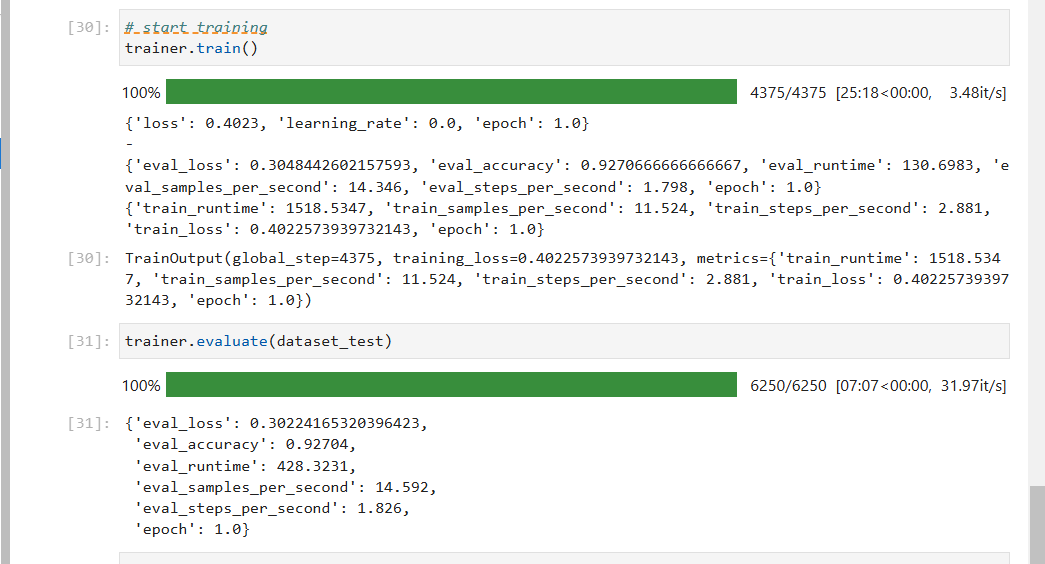
昇思大模型平台打卡体验活动:项目2基于MindSpore通过GPT实现情感分类
昇思大模型平台打卡体验活动:项目2基于MindSpore通过GPT实现情感分类 1. 载入与处理数据集 在情感分类任务中,我们使用了IMDB数据集,首先需要对数据进行加载和处理。由于原数据集没有验证集,我们将训练集重新划分为训练集和验证…...

【JAVA】会员等级互通匹配数据库表设计
1、使用数据库:mysql数据库 设计四张表: 会员互通合作商配置表 会员互通合作商会员等级配置表 会员互通合作日志表 会员互通合作等级映射表 CREATE TABLE user_level_partner ( id bigint NOT NULL AUTO_INCREMENT, partner_novarchar(100) DE…...

论文阅读:基于语义分割的非结构化田间道路场景识别
论文地址:DOI: 10.11975/j.issn.1002-6819.2021.22.017 概要 环境信息感知是智能农业装备系统自主导航作业的关键技术之一。农业田间道路复杂多变,快速准确地识别可通行区域,辨析障碍物类别,可为农业装备系统高效安全地进行路径规…...

linux部分问题以及解决方式
目录 1.ubuntu桌面不显示了,只有命令行1.1启动gdm3服务1.2安装lightdm桌面管理包 1.ubuntu桌面不显示了,只有命令行 有如下两种解决方式。 1.1启动gdm3服务 这种方法只能临时生效,每次重启都要手动启动 sudo service gdm3 restart 1.2安装…...

qt QTreeWidget详解
1、概述 QTreeWidget 是 Qt 框架中的一个类,用于以树形结构展示数据。它基于 QTreeView 并提供了更高级别的接口,使得添加、删除和管理树形结构中的项变得更加简单。QTreeWidget 支持多级嵌套,每个项(QTreeWidgetItem)…...

注意力机制的目的:理解语义;编码器嵌入高纬空间计算;注意力得分“得到S*V”;解码器掩码和交叉注意力层用于训练;最终的编码器和输出实现大模型
目录 注意力机制的目的:理解语义中的它是小白兔 词编码器嵌入高纬空间 计算注意力得分“得到S*V” 权重QKV:连接权重 训练阶段使用解码器:翻译后的语句 解码器掩码和交叉注意力层用于训练 最终的编码器和输出实现大模型 Transformer模型中,QKV QKV的作用 举例说明…...

[java][jdk]JDK各个版本的核心特性
JDK 8至JDK 21的主要新特性概览: JDK 8 Lambda表达式:引入了函数式编程的特性,使得代码更加简洁和灵活。Stream API:提供了一种新的抽象,可以让你以声明性方式处理集合数据。新的日期和时间API:引入了jav…...

双十一”买买买!法官告诉你注意这些法律问题
“双十一”等购物节来临之际,某些电商平台为了吸引消费者提前下单预订商品,通过大力宣传付定金可享受更多优惠等方式开启预售模式。那么,如果消费者在支付定金后,因各种原因最终没有支付尾款,能否要求商家退还定金&…...

PyQt5
基于PyQt5的重绘机制实现加载页面 效果预览代码说明控件初始化超时回调重绘事件缩放事件 代码获取 效果预览 直接看图,效果展现为跟随黑点顺时针转动,且有明暗变化 代码说明 控件初始化 initUI主要用于初始化用户界面(UI)。它创建了一个具有特定样式…...
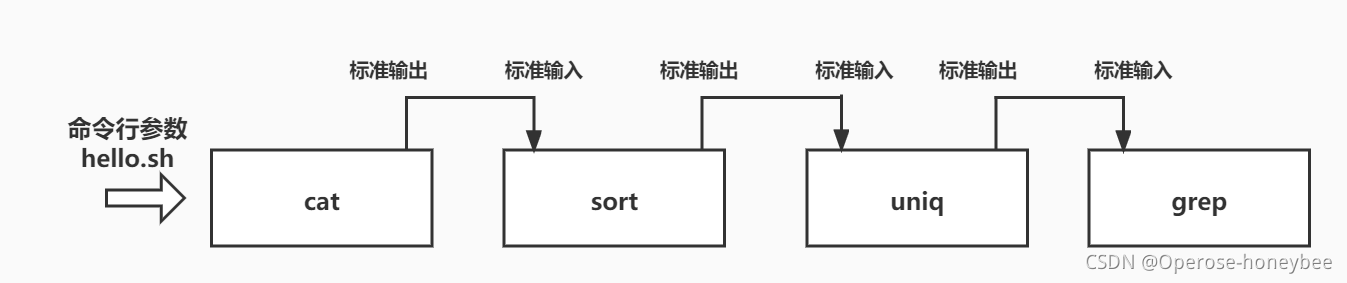
【Linux】常用命令(2.6万字汇总)
文章目录 Linux常用命令汇总1. 基础知识1.1. Linux系统命令行的含义1.2. 命令的组成 2. 基础知识2.1. 关闭系统2.2. 关闭重启2.3. 帮助命令(help)2.4. 命令说明书(man)2.5. 切换用户(su)2.6.历史指令 3.目录…...

Vue3-06_路由
路由 后台路由是根据请求url,匹配请求处理的后台模块(路径) 前台根据访问路径,决定显示的内容。 路由就是: 访问hash 与内容的对应关系 路由的工作方式 用户点击页面的路由链接导致url地址栏中的Hash值发生了变化前…...

物理验证Calibre LVS | SMIC Process过LVS时VNW和VPW要如何做处理?
SMIC家工艺的数字后端实现PR chipfinish写出来的带PG netlist如下图所示。我们可以看到标准单元没有VNW和VPW pin的逻辑连接关系。 前几天小编在社区星球上分享了T12nm ananke_core CPU低功耗设计项目的Calibre LVS案例,就是关于标准单元VPP和VBB的连接问题。 目前…...

量化分析工具日常操作日记-5-通合科技
使用量化分析微信小程序工具“梦想兔企业智能风险分析助手”日常操作日记-5-军工-通合科技(300491)。 周末国家新政策,要大力支持军工行业,我用工具挖掘了两个低位股,供大家参考。通合科技(300491ÿ…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

拟合问题处理
在机器学习中,核心任务通常围绕模型训练和性能提升展开,但你提到的 “优化训练数据解决过拟合” 和 “提升泛化性能解决欠拟合” 需要结合更准确的概念进行梳理。以下是对机器学习核心任务的系统复习和修正: 一、机器学习的核心任务框架 机…...
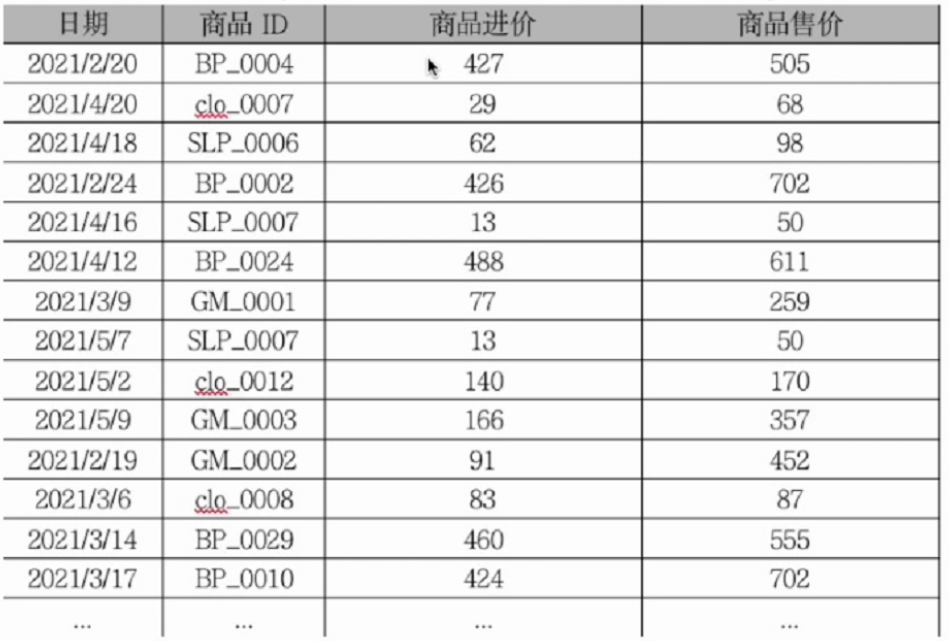
智警杯备赛--excel模块
数据透视与图表制作 创建步骤 创建 1.在Excel的插入或者数据标签页下找到数据透视表的按钮 2.将数据放进“请选择单元格区域“中,点击确定 这是最终结果,但是由于环境启不了,这里用的是自己的excel,真实的环境中的excel根据实训…...
)
GitHub 常见高频问题与解决方案(实用手册)
1.Push 提示权限错误(Permission denied) 问题: Bash Permission denied (publickey) fatal: Could not read from remote repository. 原因: 没有配置 SSH key 或使用了 HTTPS 而没有权限…...

安宝特案例丨寻医不再长途跋涉?Vuzix再次以AR技术智能驱动远程医疗
加拿大领先科技公司TeleVU基于Vuzix智能眼镜打造远程医疗生态系统,彻底革新患者护理模式。 安宝特合作伙伴TeleVU成立30余年,沉淀医疗技术、计算机科学与人工智能经验,聚焦医疗保健领域,提供AR、AI、IoT解决方案。 该方案使医疗…...
