【算法】(Python)动态规划
动态规划:
- dynamic programming。"programming"指的是一种表格法,而非编写计算机程序。
- 通常解决最优化问题(optimization problem)。
- 将问题拆分成若干个子问题,求解各子问题来得到原问题的解。
- 适用于多阶段决策(以时间划分阶段的动态过程,可人为引进时间因素)。即一个活动过程可划分多个互相关联的阶段,每个阶段都需做决策,一个阶段的决策影响下一个阶段的决策,从而确定一个活动路线(即策略,每个阶段的决策组成的序列)。
- 使用条件:最优子结构(一个问题最优解包含其子问题的最优解),重叠子问题(问题的递归算法会反复求解相同的子问题,而不是一直生成新的子问题)。
- 每个子问题只计算一次,即有一个表记录每个子问题的解,再次需要该子问题时直接查表,无需重复计算。
- 两种方法:带备忘的自顶向下(递归。从整体开始,拆分多个子问题递归求解),自底向上(迭代。先解决最小问题,进而解决整体问题)。通常使用自底向上。
- 关键:解决冗余,以空间换时间(占用额外的内存,但节省计算时间)。
- 缺点:“维数障碍”(维度增加,空间复杂程度呈指数级增长),没有统一的处理方法(具体问题具体分析)。
动态规划、分治方法、贪心算法,都是将问题分成若干个子问题,求解子问题从而得到原问题的解。
动态规划与分治方法的区别:
- 动态规划的子问题相互重叠、不是独立的。分治方法的子问题互不相交、相互独立。
- 动态规划的子问题只计算一次,并保存子问题的解。分治方法会计算每次出现的子问题。若同样的问题使用分治方法,则会重复计算相同的子问题。
动态规划与贪心算法的区别:
- 动态规划寻求全局最优解(相关的子问题全部解决了,才能做出选择)。贪心算法是贪心地追求局部最优解(即当前状态下最优选择,求解选出的子问题的解),不一定全局最优解。
案例:
1、(难度:简单)【力扣】746. 使用最小花费爬楼梯

解题思路:台阶0和台阶1均可为起始点(即花费为0),此后,到达各台阶(含目的地)的最小花费:min(前1个台阶走1步到达的最小花费,前2个台阶走2步到达的最小花费)。有一个列表记录到达各台阶(含目的地)的最小累积花费。
知识点:min(a, b):从a和b中获取最小值。
class Solution:def minCostClimbingStairs(self, cost: List[int]) -> int:n = len(cost) # 数组长度res = [0] * (n + 1) # 记录到达各台阶和目的地的累积花费 # 从下标为0或1开始,花费为0,忽略# 从下标为2开始,判断前1个台阶到这和前2个台阶到这的累积最小花费,添加到结果列表中for i in range(2, n + 1):res[i] = min(res[i - 1] + cost[i - 1], res[i - 2] + cost[i - 2])# 返回到达目的地时的累积花费return res[n]优化:各台阶(含目的地)花费涉及:前1个台阶走1步的花费,前2个台阶走2步的花费,其中最小的值。
设置3个变量:prev(当前台阶的前1个台阶,走2步到下一个需到达的台阶),curr(当前台阶,走1步到下一个需到达的台阶),next(下一个需到达的台阶)。
返回:最终到达当前台阶的累积最小花费。
class Solution:def minCostClimbingStairs(self, cost: List[int]) -> int:n = len(cost) # 数组长度prev, curr = 0, 0 # prev:前1个台阶,curr:当前台阶# 从下标为0或1开始,花费为0,忽略# 从下标为2开始,计算到达该台阶的累积花费# 当前台阶走1步到下一个台阶和前1个台阶走2步到下一个台阶的累积最小花费for i in range(2, n + 1):next = min(curr + cost[i - 1], prev + cost[i - 2])prev, curr = curr, next # 向后滚动移动return currpython中itertools模块中pairwise可依次生成连续的两个元素。
itertools.pairwise(可迭代对象):返回迭代器,迭代器中为依次生成的连续的2个元素。

class Solution:def minCostClimbingStairs(self, cost: List[int]) -> int:n = len(cost) # 数组长度prev, curr = 0, 0 # prev:前1个台阶,curr:当前台阶# 从下标为0或1开始,花费为0,忽略# 从下标为2开始,计算到达该台阶的累积花费# 当前台阶走1步到下一个台阶和前1个台阶走2步到下一个台阶的累积最小花费import itertoolsfor a, b in itertools.pairwise(cost):next = min(prev + a, curr + b)prev, curr = curr, next # 向后滚动移动return curr2、(难度:中等)【力扣】714. 买卖股票的最佳时机含手续费

解题思路:有一个二维数组,记录每一日最大收益:max(若当日手上没有股票时的最大收益,若当日手上有股票时的最大收益)。
知识点:[ [ 0,0] ] * n:二维数组,有n个元素,元素类型仍为数组。即[[0,0],[0,0],...,[0,0]]。
二维数组[0][1]:获取二维数组的第一个元素中下标为1的值。
max(a, b):从a和b中获取最大值。
class Solution:def maxProfit(self, prices: List[int], fee: int) -> int:n = len(prices)# 二维数组初始化,记录[第i日手上没股票的收益,第i日手上有股票的收益]res = [[0, 0]] * n# 第1日(res列表中下标为0的元组),下标为0的值为0(第1日手上没有股票的收益),忽略# 第1日(res列表中下标为0的元组),下标为1的值为付出的买入价(第1日手上有股票的收益)res[0][1] = -prices[0] # 遍历每日价格for i in range(1, n):# 当日,手上没有股票的收益:前1日也没股票,前1日有股票今天卖掉,取最大值res[i][0] = max(res[i - 1][0], res[i - 1][1] + prices[i] - fee)# 当日,手上有股票的收益:前1日也有股票,前1日没股票今天买入,取最大值res[i][1] = max(res[i - 1][1], res[i - 1][0] - prices[i])# 最后,手上没有股票收益更大return res[n - 1][0]优化:今日收益涉及前1日手上是否有股票。滚动记录。
设置2个变量:zero(当日若手上没有股票时的收益)。one(当日若手上有股票时的收益)。
返回最终手上没有股票时的收益。
class Solution:def maxProfit(self, prices: List[int], fee: int) -> int:n = len(prices)# 第1日,zero:手上没有股票的收益,one:手上有股票的收益(付出的买入价)zero, one = 0, -prices[0]# 遍历每日价格for i in (range(1, n)):# 当日,手上没有股票的收益:前1日也没股票,前1日有股票今天卖掉,取最大值zero = max(zero, one + prices[i] - fee)# 当日,手上有股票的收益:前1日也有股票,前1日没有股票今天买入,取最大值one = max(one, zero - prices[i])# 最后,手上没有股票,收益最大return zero注:本题其他解题方法:贪心算法
3、(难度:困难)【力扣】871. 最低加油次数

解题思路:遍历每个加油站,先假设每到一个加油站都加油,i个加油站最多加油 i 次。
要求加油次数尽可能少,为避免重复加油,依次减少到达该加油站的加油次数(j从i到0),滚动调整加油 j 次后可行驶最大距离:max(已加油 j次 在本加油站不加油的最大距离,已加油 j-1次 在本加油站加油后最大距离)。
最后遍历加油 j次后可行驶的最大距离,大于等于目的地的距离,则返回下标即加了几次油,否则无法到达目的地返回-1。
知识点:enumerate(可迭代对象):返回所有的元素下标和元素内容,元组形式。一般用于for循环。
class Solution:def minRefuelStops(self, target: int, startFuel: int, stations: List[List[int]]) -> int: res = [0] * (len(stations) + 1) # 记录每次加油后(含初始油量)可以行使的最大距离 res[0] = startFuel # 初始油量可以行使的最大距离# 遍历每个加油站for i, (long, fuel) in enumerate(stations):# 先假设每到一个加油站就加油,再减少到这的加油次数,滚动调整加油j次(i到0)后可行使的最大距离# 例如到达第3个加油站后最多加油3次:# 若加油3次最大行驶距离:max(已加油3次本次不加油最大距离, 已加油2次本次再加油后最大距离)# 若加油2次最大行驶距离:max(已加油2次本次不加油最大距离, 已加油1次本次再加油后最大距离)# 若加油1次最大行驶距离:max(已加油1次本次不加油最大距离, 已加油0次本次再加油后最大距离) for j in range(i, -1, -1): # 倒序,避免重复加油# 到达加油站后,才判断在这是否加油,以及加油j次后可行驶最大距离if res[j] >= long:res[j + 1] = max(res[j + 1], res[j] + fuel)# 遍历加油j次后的最大行使距离,超过目的地则返回下标即加了几次油for j, val in enumerate(res):if val >= target: return jreturn -1注:本题其他解题方法:贪心算法
相关文章:

【算法】(Python)动态规划
动态规划: dynamic programming。"programming"指的是一种表格法,而非编写计算机程序。通常解决最优化问题(optimization problem)。将问题拆分成若干个子问题,求解各子问题来得到原问题的解。适用于多阶段…...

EasyExcel 学习之 导出 “提示问题”
EasyExcel 学习之 导出 “提示问题” 现象分析解决(伪代码)前端 POST 实现后端实现 现象 EasyExcel 支持导出 xlsx、xls、csv 三种文件格式。在导出过程中可能发生各种异常,当发生异常时应该提示错误信息而非导出一个错误的文件。 分析 首…...
低功耗四运算放大器LM324N)
应用系统开发(3)低功耗四运算放大器LM324N
LM324N 是一种广泛使用的 低功耗四运算放大器,由德州仪器(Texas Instruments)和其他制造商生产。它具有四个独立的运算放大器,能够在单电源或双电源模式下运行,适合多种模拟电路应用。以下是详细信息: 芯片基本信息 型号:LM324N封装类型:常见 DIP(双列直插封装)或 SO…...

基于微信小程序的电商平台+LW示例参考
1.项目介绍 系统角色:管理员、普通用户功能模块:管理员(用户管理、商品分类、商品管理、订单管理、系统管理等),普通用户(个人中心、收藏、我的订单、查看商品等)技术选型:SpringBo…...

[Android] Graphic Buffer 的申请
前言: MediaCodec 支持 texture mode,即MediaCodec解码video完毕后把 yuv 数据填入 GPU 共享出来的 graphic buffer 里面,app 会把 video 的 yuv数据 和 ui 的数据通过通过软件渲染组件(opengl等)发送给GPU 进行一并渲染。这样做的效率较低&…...

【大数据学习 | HBASE高级】storeFile文件的合并
Compaction 操作分成下面两种: Minor Compaction:是选取一些小的、相邻的StoreFile将他们合并成一个更大的StoreFile,对于删除、过期、多余版本的数据不进行清除。 Major Compaction:是指将所有的StoreFile合并成一个StoreFile&am…...

多平台编包动态引入依赖的解决方案
最近开发时遇到了这样的需求,A 平台需要引入一个 video.js,B 平台却是不需要的,那么面向 B 平台打包的时候把依赖装进去自然就不大合适。最好的方法是动态引入依赖,根据平台来判断要不要引入 动态引入依赖 很快啊,动…...

[单例模式]
目录 [设计模式] 单例模式 1. 饿汉模式 2. 懒汉模式 3. 单例模式的线程安全问题 [设计模式] 设计模式是软件工程中的一种常见做法, 它可以理解为"模板", 是针对一些常见的特定场景, 给出的一些比较好的固定的解决方案. 不同语言适用的设计模式是不一样的. 这里…...

速盾:游戏盾的功能和原理详解
速盾有一款专注于网络游戏安全的防护系统,它通过实时监测游戏网络流量和玩家行为,以及使用先进的算法和技术进行分析和识别,检测出各种外挂、作弊行为和恶意攻击,从而保障游戏的公平性和玩家的安全性。 速盾游戏盾的主要功能包括…...

Spleeter:音频分离的革命性工具
目录 什么是Spleeter?Spleeter的工作原理Spleeter的应用场景Spleeter的技术优势Spleeter的挑战与局限性结论 什么是Spleeter? Spleeter 是一个由 Deezer 开发的开源音频源分离工具。它基于深度学习技术,尤其是卷积神经网络(CNN&a…...

【笔记】自动驾驶预测与决策规划_Part6_不确定性感知的决策过程
文章目录 0. 前言1. 部分观测的马尔可夫决策过程1.1 POMDP的思想以及与MDP的联系1.1.1 MDP的过程回顾1.1.2 POMDP定义1.1.3 与MDP的联系及区别POMDP 视角MDP 视角决策次数对最优解的影响 1.2 POMDP的3种常规解法1.2.1 连续状态的“Belief MDP”方法1. 信念状态的定义2. Belief …...

openresty入门教程:access_by_lua_block
在OpenResty中,access_by_lua_block 是一个功能强大的指令,它允许你在Nginx的访问控制阶段执行Lua脚本。这个阶段发生在Nginx处理请求的过程中,紧接在rewrite阶段之后,但在请求被传递到后端服务器(如PHP、Node.js等&am…...

Caused by: org.apache.flink.api.common.io.ParseException: Row too short:
Flink版本 1.17.2 错误描述 Caused by: org.apache.flink.api.common.io.ParseException: Row too short: 通过flink中的flinkSql直接使用对应的connector去获取csv文件内容,报获取的数据太短了 可能原因 1.创建的表字段多于csv文件当中的表头 定位 在获取csv…...

hbase的安装与简单操作
好的,这里是关于 HBase 的安装和基本操作的详细步骤,分成几个更清晰的阶段: 第一部分:安装和配置 HBase 1. 环境准备 HBase 依赖于 Hadoop,因此首先确保 Hadoop 已经正确安装和配置。如果没有安装,请先下…...

PySpark本地开发环境搭建
一.前置事项 请注意,需要先实现Windows的本地JDK和Hadoop的安装。 二.windows安装Anaconda 资源:Miniconda3-py38-4.11.0-Windows-x86-64,在window使用的Anaconda资源-CSDN文库 右键以管理员身份运行,选择你的安装路径&#x…...

【进阶】Stable Diffusion 插件 Controlnet 安装使用教程(图像精准控制)
Stable Diffusion WebUI 的绘画插件 Controlnet 最近更新了 V1.1 版本,发布了 14 个优化模型,并新增了多个预处理器,让它的功能比之前更加好用了,最近几天又连续更新了 3 个新 Reference 预处理器,可以直接根据图像生产…...

调试、发布自己的 npm 包
查看 npm 的配置 npm config ls登录 whoami 查看当前登录的用户 npm whoamiaduser 登录 adduser 有以下参数: –scope 作用域–registry 注册地址 默认地址:https://registry.npmjs.org/,也可通过.npmrc文件配置 npm login 是 …...

拓扑学与DNA双螺旋结构的奇妙连接:从算法到分子模拟
拓扑的形变指的是通过连续地拉伸、弯曲或扭曲物体而不进行撕裂或粘合来改变其形状的一种数学变换。拓扑形变属于拓扑学的一个分支,研究在这些操作下保持不变的性质。简单来说,它关注的是物体“形状的本质”,而不是具体的几何形状。 拓扑形变…...
单表查询)
mysql数据库(四)单表查询
单表查询 文章目录 单表查询一、单表查询1.1 简单查询1.2where1.3group by1.4having1.5order by1.6limit 一、单表查询 记录的查询语法如下: SELECT DISTINCT(去重) 字段1,字段2… FROM 表名 WHERE 筛选条件 GROUP BY 分组 HAVING 分组筛选 ORDER BY 排序 LIMIT 限…...
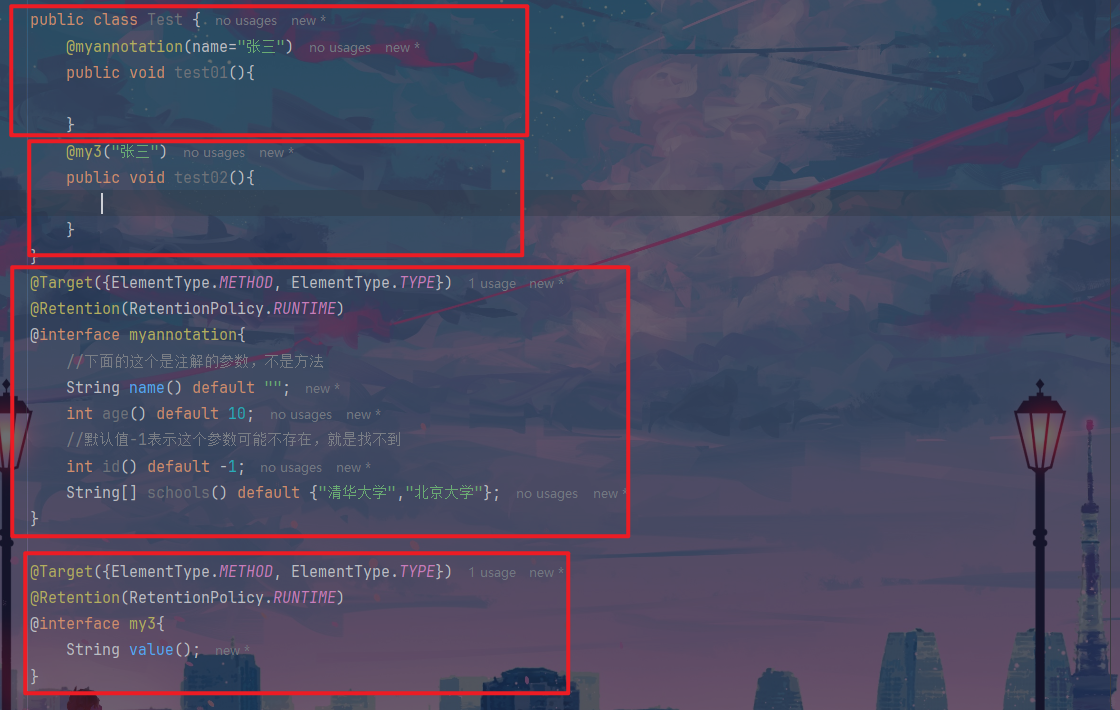
JavaEE初阶---properties类+反射+注解
文章目录 1.配置文件properities2.快速上手3.常见方法3.1读取配置文件3.2获取k-v值3.3修改k-v值3.4unicode的说明 4.反射的引入4.1传统写法4.2反射的写法(初识)4.3反射的介绍4.4获得class类的方法4.5所有类型的class对象4.6类加载过程4.7类初始化的过程4…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...
