DAY23|回溯算法Part02|LeetCode: 39. 组合总和 、40.组合总和II 、131.分割回文串
目录
LeetCode: 39. 组合总和
基本思路
C++代码
LeetCode: 40.组合总和II
基本思路
C++代码
LeetCode: 131.分割回文串
基本思路
C++代码
LeetCode: 39. 组合总和
力扣代码链接
文字讲解:LeetCode: 39. 组合总和
视频讲解:带你学透回溯算法-组合总和

基本思路
本题没有数量要求,可以无限重复,但是有总和的限制,所以间接的也是有个数的限制。将搜索过程抽象为以下树形结构:

- 递归函数参数
这里依然是定义两个全局变量,二维数组result存放结果集,数组path存放符合条件的结果。
参数:包括给定的集合candidates, 和目标值target,还定义了int型的sum变量来统计单一结果path里的总和以及设置for循环起始位置的startIndex。
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& candidates, int target, int sum, int startIndex)- 递归终止条件
终止只有两种情况,sum大于target和sum等于target。sum等于target的时候,需要收集结果。
if (sum > target) {return;
}
if (sum == target) {result.push_back(path);return;
}- 单层搜索的逻辑
单层for循环依然是从startIndex开始,搜索candidates集合。
for (int i = startIndex; i < candidates.size(); i++) {sum += candidates[i];path.push_back(candidates[i]);backtracking(candidates, target, sum, i); // 关键点:不用i+1了,表示可以重复读取当前的数sum -= candidates[i]; // 回溯path.pop_back(); // 回溯
}- 剪枝优化
对于sum已经大于target的情况,其实是依然进入了下一层递归,只是下一层递归结束判断的时候,会判断sum > target的话就返回。其实如果已经知道下一层的sum会大于target,就没有必要进入下一层递归了。那么可以在for循环的搜索范围上做做文章了。
对总集合排序之后,如果下一层的sum(就是本层的 sum + candidates[i])已经大于target,就可以结束本轮for循环的遍历。

所以我们对for循环的剪枝如下:
for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++)C++代码
class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {if (sum == target) {result.push_back(path);return;}// 如果 sum + candidates[i] > target 就终止遍历for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {sum += candidates[i];path.push_back(candidates[i]);backtracking(candidates, target, sum, i);sum -= candidates[i];path.pop_back();}}
public:vector<vector<int>> combinationSum(vector<int>& candidates, int target) {result.clear();path.clear();sort(candidates.begin(), candidates.end()); // 需要排序backtracking(candidates, target, 0, 0);return result;}
};LeetCode: 40.组合总和II
力扣代码链接
文字讲解:LeetCode: 40.组合总和II
视频讲解:回溯算法中的去重,树层去重树枝去重,你弄清楚了没?

基本思路
这个题和上个题主要存在两个不同点:本题中candidates 中的每个数字在每个组合中只能使用一次以及本题数组candidates的元素是有重复的,而上一题是无重复元素的数组candidates
如果我们还按照上一题的方法,就极有可能会获得重复的结果,那么我们应该怎么对结果进行去重呢?都知道组合问题可以抽象为树形结构,那么“使用过”在这个树形结构上是有两个维度的,一个维度是同一树枝上使用过,一个维度是同一树层上使用过。所以我们要去重的是同一树层上的“使用过”,同一树枝上的都是一个组合里的元素,不用去重。
另外,我们在树层去重的时候要对数组进行排序。
- 递归函数参数
此题还需要加一个bool型数组used,用来记录同一树枝上的元素是否使用过。
vector<vector<int>> result; // 存放组合集合
vector<int> path; // 符合条件的组合
void backtracking(vector<int>& candidates, int target, int sum, int startIndex, vector<bool>& used) - 递归终止条件
终止条件为 sum > target 和 sum == target。
if (sum > target) { // 这个条件其实可以省略return;
}
if (sum == target) {result.push_back(path);return;
}- 单层搜索的逻辑
如果candidates[i] == candidates[i - 1] 并且 used[i - 1] == false,就说明:前一个树枝,使用了candidates[i - 1],也就是说同一树层使用过candidates[i - 1]。此时for循环里就应该做continue的操作。

我在图中将used的变化用橘黄色标注上,可以看出在candidates[i] == candidates[i - 1]相同的情况下:
- used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
- used[i - 1] == false,说明同一树层candidates[i - 1]使用过
这一块的去重逻辑很抽象,一定要好好思考或者去听视频讲解去理解其中的含义。
for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {// used[i - 1] == true,说明同一树枝candidates[i - 1]使用过// used[i - 1] == false,说明同一树层candidates[i - 1]使用过// 要对同一树层使用过的元素进行跳过if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {continue;}sum += candidates[i];path.push_back(candidates[i]);used[i] = true;backtracking(candidates, target, sum, i + 1, used); // 和39.组合总和的区别1:这里是i+1,每个数字在每个组合中只能使用一次used[i] = false;sum -= candidates[i];path.pop_back();
}C++代码
class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& candidates, int target, int sum, int startIndex, vector<bool>& used) {if (sum == target) {result.push_back(path);return;}for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {// used[i - 1] == true,说明同一树枝candidates[i - 1]使用过// used[i - 1] == false,说明同一树层candidates[i - 1]使用过// 要对同一树层使用过的元素进行跳过if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {continue;}sum += candidates[i];path.push_back(candidates[i]);used[i] = true;backtracking(candidates, target, sum, i + 1, used); // 和39.组合总和的区别1,这里是i+1,每个数字在每个组合中只能使用一次used[i] = false;sum -= candidates[i];path.pop_back();}}public:vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {vector<bool> used(candidates.size(), false);path.clear();result.clear();// 首先把给candidates排序,让其相同的元素都挨在一起。sort(candidates.begin(), candidates.end());backtracking(candidates, target, 0, 0, used);return result;}
};
LeetCode: 131.分割回文串
力扣代码链接
文字讲解:LeetCode: 131.分割回文串
视频讲解:带你学透回溯算法-分割回文串

基本思路
我们来分析一下切割,其实切割问题类似组合问题。
例如对于字符串abcdef:
- 组合问题:选取一个a之后,在bcdef中再去选取第二个,选取b之后在cdef中再选取第三个.....。
- 切割问题:切割一个a之后,在bcdef中再去切割第二段,切割b之后在cdef中再切割第三段.....。
而分割问题同样可以抽象为树形结构,递归用来纵向遍历,for循环用来横向遍历:

- 递归函数参数
全局变量数组path存放切割后回文的子串,二维数组result存放结果集。
参数:本题递归函数参数还需要startIndex,因为切割过的地方,不能重复切割,和组合问题也是保持一致的。
vector<vector<string>> result;
vector<string> path; // 放已经回文的子串
void backtracking (const string& s, int startIndex)- 递归函数终止条件
切割线切到了字符串最后面,说明找到了一种切割方法,此时就是本层递归的终止条件。在处理组合问题的时候,递归参数需要传入startIndex,表示下一轮递归遍历的起始位置,这个startIndex就是切割线。
void backtracking (const string& s, int startIndex) {// 如果起始位置已经大于s的大小,说明已经找到了一组分割方案了if (startIndex >= s.size()) {result.push_back(path);return;}
}- 单层搜索的逻辑
递归循环中如何截取子串?
在for (int i = startIndex; i < s.size();i++)循环中,我们定义了起始位置startIndex,那么 [startIndex, i] 就是要截取的子串。首先判断这个子串是不是回文,如果是回文,就加入在vector<string> path中,path用来记录切割过的回文子串。
for (int i = startIndex; i < s.size(); i++) {if (isPalindrome(s, startIndex, i)) { // 是回文子串// 获取[startIndex,i]在s中的子串string str = s.substr(startIndex, i - startIndex + 1);path.push_back(str);} else { // 如果不是则直接跳过continue;}backtracking(s, i + 1); // 寻找i+1为起始位置的子串path.pop_back(); // 回溯过程,弹出本次已经添加的子串
}注意切割过的位置,不能重复切割,所以,backtracking(s, i + 1); 传入下一层的起始位置为i + 1。
当然,我们需要一个判断是否为回文子串的函数,很容易想到前面提到过的双指针法。
bool isPalindrome(const string& s, int start, int end) {for (int i = start, j = end; i < j; i++, j--) {if (s[i] != s[j]) {return false;}}return true;}C++代码
class Solution {
private:vector<vector<string>> result;vector<string> path; // 放已经回文的子串void backtracking (const string& s, int startIndex) {// 如果起始位置已经大于s的大小,说明已经找到了一组分割方案了if (startIndex >= s.size()) {result.push_back(path);return;}for (int i = startIndex; i < s.size(); i++) {if (isPalindrome(s, startIndex, i)) { // 是回文子串// 获取[startIndex,i]在s中的子串string str = s.substr(startIndex, i - startIndex + 1);path.push_back(str);} else { // 不是回文,跳过continue;}backtracking(s, i + 1); // 寻找i+1为起始位置的子串path.pop_back(); // 回溯过程,弹出本次已经添加的子串}}bool isPalindrome(const string& s, int start, int end) {for (int i = start, j = end; i < j; i++, j--) {if (s[i] != s[j]) {return false;}}return true;}
public:vector<vector<string>> partition(string s) {result.clear();path.clear();backtracking(s, 0);return result;}
};相关文章:

DAY23|回溯算法Part02|LeetCode: 39. 组合总和 、40.组合总和II 、131.分割回文串
目录 LeetCode: 39. 组合总和 基本思路 C代码 LeetCode: 40.组合总和II 基本思路 C代码 LeetCode: 131.分割回文串 基本思路 C代码 LeetCode: 39. 组合总和 力扣代码链接 文字讲解:LeetCode: 39. 组合总和 视频讲解:带你学透回溯算法-组合总和…...

go map
1、数据结构 // A header for a Go map. type hmap struct {// Note: the format of the hmap is also encoded in cmd/compile/internal/reflectdata/reflect.go.// Make sure this stays in sync with the compilers definition.count int // # live cells size of map.…...
)
三十七、Python基础语法(异常)
在 Python 中,异常是在程序执行过程中发生的错误情况。当出现异常时,程序的正常执行流程会被中断,并尝试寻找相应的异常处理机制来处理这个错误。 一、异常的类型 Python 中有很多内置的异常类型,例如: ZeroDivision…...

ThreadLocal的熟悉与使用
目录 1.ThreadLocal介绍2.ThreadLocal源码解析2.1 常用方法2.2 结构设计2.3 类图2.4 源码分析2.4.1 set方法分析2.4.2 get方法分析2.4.3 remove方法分析 3.ThreadLocal内存泄漏分析3.1 相关概念3.1.1 内存溢出3.1.2 内存泄漏3.1.3 强引用3.1.4 弱引用 3.2 内存泄漏是否和key使用…...
如何使用 Puppeteer 和 Browserless 抓取亚马逊产品数据?
您可以在亚马逊上找到所有有关产品、卖家、评论、评分、特价、新闻等的相关且有价值的信息。无论是卖家进行市场调研还是个人收集数据,使用高质量、便捷且快速的工具将极大地帮助您准确地抓取亚马逊上的各种信息。 为什么抓取亚马逊产品数据很重要? 亚…...

使用Python求解经典“三门问题”,揭示概率的奇妙之处
三门问题(Monty Hall Problem)是经典的概率问题,描述了一位游戏选手在三个门中选择一扇门,其中一扇门后有奖品,其余两扇门后是空的。选手做出选择后,主持人会打开另一扇空门,然后给选手一次更改…...
 . DDL)
数据库基础(6) . DDL
3.2.DDL 数据定义语言 DDL : Data Definition Language 用于创建新的数据库、模式(schema)、表(tables)、视图(views)以及索引(indexes)等。 常见的DDL语句包括SHOW、CREATE、DRO…...

2024 年度分布式电力推进(DEP)系统发展探究
分布式电力推进 (DEP) 的发明是为了尝试和改进现代飞机:我们如何提高飞机的效率?提高它的机动性?缩短它的起飞和着陆距离? DEP 概念有望在提高性能的同时减少燃料消耗,在我们孜孜不倦地努力使航…...

vue通过iframe方式嵌套grafana图表
文章目录 前言一、iframe方式实现xxx.xxx.com拒绝连接登录不跳转Cookie 的SameSite问题解决不显示额外区域(kiosk1) 前言 我们的前端是vue实现的,监控图表是在grafana中的,需要在项目web页面直接显示grafana图表 一、iframe方式实现 xxx.xxx.com拒绝连…...

简单介绍下 Java 中的 @Validated 和 @Valid 注解的区别?
文章目录 Valid:专注单个对象的深度验证适用场景使用示例小结 Validated:聚焦接口分组的批量验证适用场景使用示例小结 主要区别总结如何选择?总结推荐阅读文章 在 Java 开发中,为了确保输入数据符合我们的要求,少不了…...

SpringBoot配置Rabbit中的MessageConverter对象
SpringAMQP默认使用SimpleMessageConverter组件对消息内容进行转换 SimpleMessageConverter: only supports String, byte[] and Serializable payloads仅仅支持String、Byte[]和Serializable对象Jackson2JsonMessageConverter:was expecting (JSON Str…...

C++ 错题本--duplicate symbol问题
顾名思义, duplicate symbol是重复符号的意思! 代码是用来做什么的(问题缘由 & 代码结构) 写排序算法, 提出了一个公共的头文件用来写一些工具方法, 比如打印数组内容. 以便于不同文件代码需要打印数组内容的时候,直接引入相关头文件即可, 但是编译时出现了 duplicate sym…...

Cursor的chat与composer的使用体验分享
经过一段时间的试用,下面对 Composer 与 Chat 的使用差别进行总结: 一、长文本及程序文件处理方面 Composer 在处理长文本时表现较为稳定,可以对长文进行更改而不会出现内容丢失的情况。而 Chat 在更改长的程序文件时,有时会删除…...

【优选算法 — 滑动窗口】最大连续1的个数 将 x 减到0的最小操作数
最大连续1的个数 最大连续1的个数 题目描述 题目解析 给我们一个元素全是0或者1的数组,和一个整数 k ,然后让我们在数组选出最多的 k 个0;这里翻转最多 k 个0的意思,是翻转 0 的个数< k,而不是一定要翻转 k …...

《TCP/IP网络编程》学习笔记 | Chapter 8:域名及网络地址
《TCP/IP网络编程》学习笔记 | Chapter 8:域名及网络地址 《TCP/IP网络编程》学习笔记 | Chapter 8:域名及网络地址域名系统什么是域名?DNS 服务器IP 地址和域名之间的转换使用域名的必要性利用域名获取 IP 地址利用 IP 地址获取域名 基于 Wi…...

FastHTML快速入门:调试模式和 URL中的变量
调试模式 FastHTML基于FastAPI友好的装饰器模式来指定URL,并添加了额外功能: main.py from fasthtml.common import * app, rt fast_app() rt("/") def get():return Titled("FastHTML", P("让我们开始吧!"…...

C++高级编程(8)
八、标准IO库 1.输入输出流类 1)非格式化输入输出 2)put #include <iostream> #include <string> using namespace std; int main() {string str "123456789";for (int i str.length() - 1; i > 0; i--) {cout.put(str[i]); //从最后一个字符开…...

AUTOSAR_EXP_ARAComAPI的7章笔记(2)
☞返回总目录 相关总结:服务发现实现策略总结 7.2 服务发现的实现策略 如前面章节所述,ara::com 期望产品供应商实现服务发现的功能。服务发现功能基本上是在 API 级别通过 FindService、OfferService 和 StopOfferService 方法定义的,协议…...
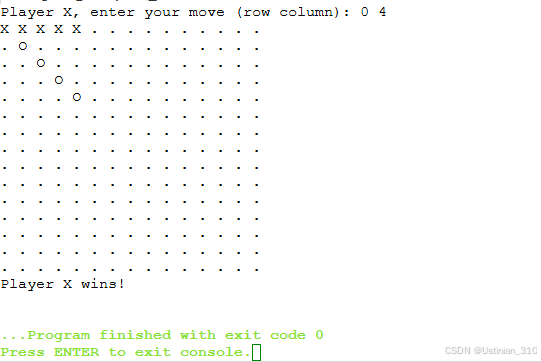
【C++】 C++游戏设计---五子棋小游戏
1. 游戏介绍 一个简单的 C 五子棋小游戏 1.1 游戏规则: 双人轮流输入下入点坐标横竖撇捺先成五子连线者胜同一坐标点不允许重复输入 1.2 初始化与游戏界面 初始化界面 X 输入坐标后 O 输入坐标后 X 先达到胜出条件 2. 源代码 #include <iostream> #i…...

仿RabitMQ 模拟实现消息队列项目开发文档2(个人项目)
项目需求分析 核心概念 现在需要将这个项目梳理清楚了,便于之后的代码实现。项目中具有一个生产消费模型: 其中生产者和消费者的个数是可以灵活改变的,让系统资源更加合理的分配。消息队列的主逻辑和上面的逻辑基本一样,只不过我…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...
