探索Dijkstra算法的普遍最优性:从经典算法到最新学术突破
引言
在计算机科学中,Dijkstra算法是解决单源最短路径问题的经典算法,尤其在地图导航、网络通信和机器人路径规划等领域有着广泛应用。近期,学术界在此算法上取得了重大突破:研究人员证明了Dijkstra算法的“普遍最优性”,即无论图结构多复杂,算法都能在最坏情况下达到理论上最优的性能。本文将深入解读Dijkstra算法的原理、应用、最新研究进展以及其普遍最优性对技术领域的影响。
一、Dijkstra算法的基本原理
Dijkstra算法由荷兰计算机科学家埃兹格·迪杰斯特拉(Edsger Dijkstra)在1956年发明。其核心目的是在图结构中找到从一个起点到其他节点的最短路径,这在现实生活中应用广泛。例如,在地图应用中帮助用户找到从当前位置到目的地的最快路径。
1.1 算法的工作机制
Dijkstra算法基于贪心思想,通过逐步扩展最短路径来构建最终的解:
- 起点设定:从起始节点开始,将其距离初始化为0,其他节点的距离设为无穷大。
- 逐步选择最短路径:算法依次选择距离最小的未访问节点,更新其邻接节点的距离。
- 路径更新:如果发现通过当前节点到达邻接节点的距离更短,则更新最短路径。
- 终止条件:重复上述步骤,直到访问完所有节点。
1.2 算法的运行示例
假设我们有以下场景:
- 从城市的中心广场(A点)出发,B点(公园)距离A点1公里,C点(商场)距离A点5公里。
- Dijkstra算法会优先选择A到B的路径,到达B点后再计算从B出发的最短路径,比如B到D(图书馆)距离1公里,那么A到D的总距离就是2公里。
这种选择最短路径、逐步扩展的方法在复杂图结构中非常高效,从而使Dijkstra算法在地图导航和通信网络中广泛应用。
二、Dijkstra算法的实际应用
2.1 地图导航系统
Dijkstra算法在Google地图、Apple地图等导航软件中应用广泛。在用户输入起点和终点后,Dijkstra算法可以通过城市道路网络的图结构快速找到最优路线,确保用户以最短时间到达目的地。
2.2 计算机网络路径规划
在计算机网络中,设备(如计算机、路由器)之间的连接可以被视为图结构的节点和边。Dijkstra算法帮助网络设备寻找最优数据传输路径,从而提高传输效率,确保数据在最短时间内传递到目的地。
2.3 机器人路径规划
在机器人技术中,Dijkstra算法也广泛应用于导航。机器人需要在复杂环境中避开障碍物,找到从起点到目标的最短路径。这对于仓储物流等场景下的自动化机器人调度尤为重要。
三、Dijkstra算法的历史背景
Dijkstra算法的诞生充满传奇色彩。1956年,年仅26岁的迪杰斯特拉在阿姆斯特丹的咖啡馆中思索最短路径算法,凭借强大的思维能力,在脑海中推演出算法的细节。随后,他发表了著名的论文《关于图的两个问题的注释》,奠定了该算法在计算机科学中的地位。
四、最新研究进展:Dijkstra算法的普遍最优性
4.1 普遍最优性的概念
最新研究表明,通过改进Dijkstra算法中的堆数据结构,使其具备“工作集属性”(Working Set Property),Dijkstra算法在任何图结构中都能表现出色,而不仅仅是在最坏情况下达到最优性能。这种改进使得算法在处理复杂图结构时能够更加高效,达到了“普遍最优性”。
4.2 工作集属性的堆数据结构
工作集属性可以理解为优先处理新插入的任务。这一改进使得Dijkstra算法能够更高效地在局部结构密集的图中运行,显著提升了算法的整体性能。
例如,研究人员设计了一种新的堆数据结构,使得在堆中插入的元素能够快速访问,这在处理局部密集或层次结构复杂的图时尤为重要。通过这种改进,Dijkstra算法的性能得到了显著提升,在最坏情况下也能达到理论上的最优性能。
4.3 理论分析与研究成果
该研究由苏黎世联邦理工学院(ETH Zurich)、卡内基梅隆大学(CMU)和普林斯顿大学等顶尖高校的研究人员联合完成,并荣获FOCS 2024最佳论文奖。这一突破不仅为Dijkstra算法提供了更加精确的复杂度分析,还为算法在实际应用中的性能提供了更高的保障。
五、Dijkstra算法普遍最优性的意义与未来展望
5.1 技术影响
Dijkstra算法在广泛的计算场景中扮演着不可或缺的角色。普遍最优性的证明意味着在未来的导航系统、网络通信等领域,可以更加放心地依赖Dijkstra算法实现最优性能。
5.2 潜在挑战
尽管工作集属性的堆结构显著提升了Dijkstra算法的性能,但在特定场景下可能存在改进的空间。例如,在高动态性的网络环境中,如何有效适应网络拓扑的快速变化依然是研究热点。
5.3 未来趋势
未来,随着图结构算法研究的深入,或许会出现更为高效的最短路径算法。同时,在智能交通、自动驾驶、物流优化等领域,普遍最优性为大规模图计算提供了理论保障,或将进一步推动相关领域的发展。
总结
Dijkstra算法的普遍最优性证明是计算机科学领域的一项重要突破,使得这项经典算法在不同场景中都能表现出最优性能。通过本文的介绍,我们了解到Dijkstra算法的工作原理、实际应用、历史背景以及最新的研究进展。未来,随着新型数据结构的持续改进,Dijkstra算法的应用场景将更加广泛,助力导航系统、计算机网络等多个领域的发展。

相关文章:

探索Dijkstra算法的普遍最优性:从经典算法到最新学术突破
引言 在计算机科学中,Dijkstra算法是解决单源最短路径问题的经典算法,尤其在地图导航、网络通信和机器人路径规划等领域有着广泛应用。近期,学术界在此算法上取得了重大突破:研究人员证明了Dijkstra算法的“普遍最优性”ÿ…...

️代码的华尔兹:在 Makefile 的指尖上舞动自动化的诗篇
文章目录 😶🌫️😶🌫️😶🌫️背景——一个优秀工程师必备技能😶🌫️😶🌫️😶🌫️一、🤩🤩快速了解…...

函数式编程Stream流(通俗易懂!!!)
目录 1.Lambda表达式 1.1 基本用法 1.2 省略规则 2.Stream流 2.1 常规操作 2.1.1 创建流 2.1.2 中间操作 filter map distinct sorted limit 编辑skip flatMap 2.1.3 终结操作 foreach count max&min collect anyMatch allMatch noneMatch …...

数据分析:转录组差异fgsea富集分析
文章目录 介绍加载R包数据链接导入数据数据预处理DE testing: 2BP vs no-BP比较limma-voomLoad steroid dataIn No-BP patientsIn 2BP patientsCompare gene expression vs bacterial mass其他系统信息介绍 转录组差异fgsea富集分析是一种基于基因集的富集分析方法,它关注的是…...
在Django中安装、配置、使用CKEditor5,并将CKEditor5录入的文章展现出来,实现一个简单博客网站的功能
在Django中可以使用CKEditor4和CKEditor5两个版本,分别对应软件包django-ckeditor和django-ckeditor-5。原来使用的是CKEditor4,python manager.py makemigrations时总是提示CKEditor4有安全风险,建议升级到CKEditor5。故卸载了CKEditor4&…...

AI笔筒操作说明及应用场景
AI笔筒由来: 在快节奏的现代办公环境中,我们一直在寻找既能提升效率、增添便利,又能融入企业文化、展现个人品味的桌面伙伴。为此,我们特推出专为追求卓越、注重细节的您设计的AI笔筒礼品版,它集高科技与实用性于一身…...
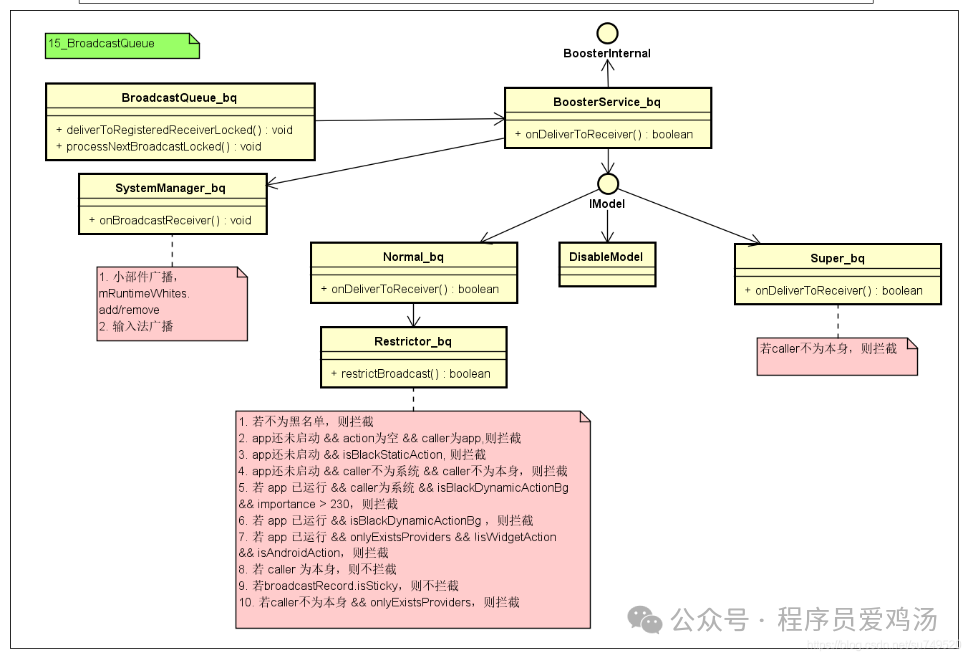
Android自启动管控
1. 自启动管控需求来源 自启动、关联启动、交叉启动、推送启动等现象的泛滥除了对个人信息保护带来隐患外,还会导致占用过多的系统CPU和内存资源,造成系统卡顿、发热、电池消耗过快;还可能引入一些包含“恶意代码”的进程在后台隐蔽启动&…...

把握鸿蒙生态崛起的机遇:开发者视角的探讨
大家好,我是程序员小羊! 前言: 近年来,鸿蒙系统(HarmonyOS)的发展备受瞩目。随着其在智能手机、智能穿戴、车载系统和智能家居等领域的广泛应用,鸿蒙系统正逐渐形成与安卓、iOS并列的三足鼎立…...

MySQL初学之旅(1)配置与基础操作
目录 1.前言 2.正文 2.1数据库的发展历程 2.2数据库的基础操作 2.2.1启动服务 2.2.2创建与删除数据库 2.2.3数据类型 2.2.4创建表与删除表 2.3MySQL Workbench基础使用简介 3.小结 1.前言 哈喽大家好吖,今天博主正式开始为大家分享数据库的学习ÿ…...
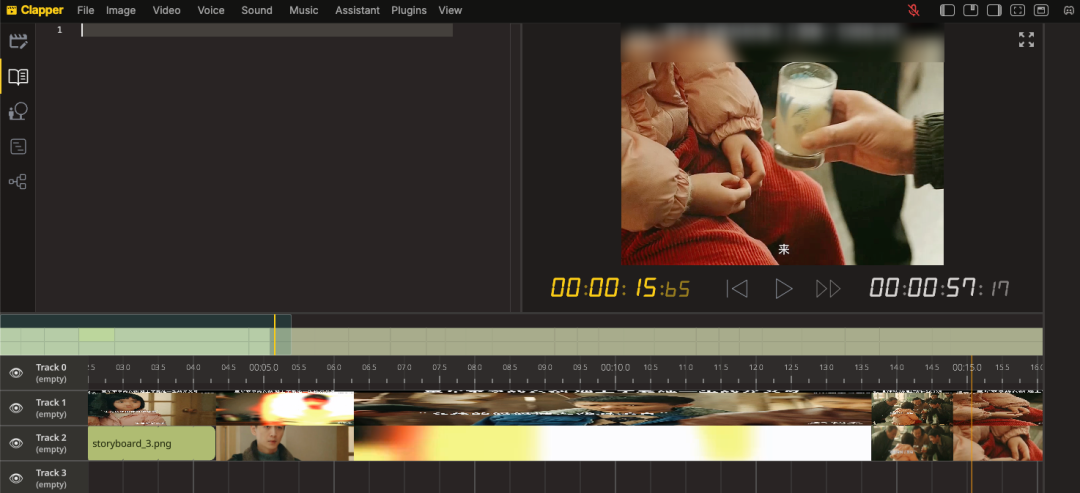
一款革命性的视频剪辑工具,AI剪辑新纪元:Clapper
如果说AI视频剪辑工具哪家强?还真想不出有什么让人眼前一亮的AI视频剪辑应用。 毕竟随着AI技术的发展越来越快,各种AI应用如雨后春笋般涌现,然而,真正能够在视频剪辑领域脱颖而出的工具却寥寥无几。 今天我要介绍的 Clapper 就是…...

HTML 区块
HTML 区块 HTML(HyperText Markup Language)是构建网页的标准语言,它定义了网页的结构和内容。在HTML中,区块元素是指那些能够定义较大块状结构的元素,比如段落、标题、列表、表格和 divis 等。这些元素通常对页面的布…...

复杂度的讲解
数据结构可以简单理解为在内存中管理数据 它具有速度快 带电存储的特点(临时存储) 如何衡量一个算法的好坏 因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。 时间复杂度主要衡量一个算…...

[ Linux 命令基础 2 ] Linux 命令详解-系统管理命令
🍬 博主介绍 👨🎓 博主介绍:大家好,我是 _PowerShell ,很高兴认识大家~ ✨主攻领域:【渗透领域】【数据通信】 【通讯安全】 【web安全】【面试分析】 🎉点赞➕评论➕收藏 养成习…...

使用docker部署Prometheus和Grafana去监控mysql和redis
自动化性能监控系统安装部署 相关工具的安装部署 服务工具分配 服务器工具端口10.0.20.9grafana300010.0.20.9prometheus909010.0.20.10mysql330610.0.20.10mysql-exporter910410.0.20.10redis330610.0.20.10redis_exporter9121 使用docker-compose安装prometheus 先拉取p…...

日志管理 | Log360 实现PCI DSS v4.0数据安全合规要求
PCI DSS 是一项网络安全标准,得到所有主要信用卡和支付处理公司的支持,旨在确保信用卡和借记卡号码的安全。最新的PCI DSS v4.0 代表支付卡行业数据安全标准。 任何依赖信用卡交易的企业都不能将数字安全视为一个偷工减料的领域,因为数据泄露…...

JAVA中的string和stringbuffer
【之前面试测试岗位的时候有被问到这个问题,面试结束后特地来学习一下】 目录 谁先被提出的String的使用StringBuffer的使用两者区别 谁先被提出的 String类先于StringBuffer被提出,作为Java语言的基础部分,而StringBuffer是为了解决实际开…...

轻型民用无人驾驶航空器安全操控------理论考试多旋翼部分笔记
官网:民用无人驾驶航空器综合管理平台 (caac.gov.cn) 说明:一是法规部分;二是多旋翼部分 本笔记全部来源于轻型民用无人驾驶航空器安全操控视频讲解平台 目录 官网:民用无人驾驶航空器综合管理平台 (caac.gov.cn) 一、轻型民用无人…...

计算用户订购率梧桐数据库和oracle数据库sql分析
一、背景说明 移动运营商平台提供多种类型的产品权益,用户可以通过订购来使用。平台需要定期统计各个产品的用户订购情况,以便了解各个产品的受欢迎程度。这些统计数据将用于优化产品、提升用户体验和制定市场推广策略。 二、表结构说明 梧桐数据库建…...

通过DNS服务器架构解释DNS请求过程
在前面的章节,这里,基于PCAP数据包和RFC文档详细介绍了DNS请求和响应的每个字段的含义。但是在现实的网络世界中,DNS请求和响应的数据包是怎么流动的,会经过哪些设备。本文将着重说明一下目前网络空间中DNS请求和响应的流动过程。 当前网络空间中比较常见DNS请求的流程如下…...

OKG Research:用户意图驱动的Web3应用变革
出品| OKG Research 作者|Samuel QIN 当前加密市场的快速演变中,用户增长成为行业可持续发展的基石。目前主流观点在推动行业前进的路上,从单纯的技术探索在向更注重应用价值的方向转变。尽管近年来Web3生态系统发展迅速…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...
