222. 完全二叉树的节点个数 迭代
222. 完全二叉树的节点个数
已解答
简单
相关标签
相关企业
给你一棵 完全二叉树 的根节点
root,求出该树的节点个数。完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第
h层,则该层包含1~ 2h个节点。示例 1:
输入:root = [1,2,3,4,5,6] 输出:6示例 2:
输入:root = [] 输出:0示例 3:
输入:root = [1] 输出:1提示:
- 树中节点的数目范围是
[0, 5 * 104]0 <= Node.val <= 5 * 104- 题目数据保证输入的树是 完全二叉树
进阶:遍历树来统计节点是一种时间复杂度为
O(n)的简单解决方案。你可以设计一个更快的算法吗?
迭代
public int countNodes(TreeNode root) {if(root == null) return 0;int m1 = countNodes(root.left);int m2 = countNodes(root.right);return m1+m2+1;}相关文章:

222. 完全二叉树的节点个数 迭代
222. 完全二叉树的节点个数 已解答 简单 相关标签 相关企业 给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。 完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值࿰…...

中心极限定理的三种形式
独立同分布的中心极限定理: 设 X 1 , X 2 , … , X n X_1, X_2, \ldots, X_n X1,X2,…,Xn是独立同分布的随机变量序列,且 E ( X i ) μ E(X_i) \mu E(Xi)μ, D ( X i ) σ 2 > 0 D(X_i) \sigma^2 > 0 D(Xi)σ2>0存在…...

React Native 全栈开发实战班 - 导航栈定制
在 React Native 应用中,导航栈管理是实现页面跳转和状态维护的核心机制。React Navigation 提供了强大的导航栈管理功能,允许开发者灵活地控制页面堆栈、传递参数、处理返回逻辑等。本章节将深入探讨导航栈的管理与定制,包括如何控制导航栈、…...

扬州BGP高防服务器可以给企业带来哪些好处?
扬州BGP服务器是目前江苏较为出名的高防机房,随着网络安全逐渐被企业所重视,扬州机房的也被大家进行选择,但是扬州BGP高防服务器除了可以帮助企业抵御网络攻击,还有着其他的帮助,下面就让我们来了解一下吧!…...

题目讲解15 合并两个排序的链表
原题链接: 合并两个排序的链表_牛客题霸_牛客网 思路分析: 第一步:写一个链表尾插数据的方法。 typedef struct ListNode ListNode;//申请结点 ListNode* BuyNode(int x) {ListNode* node (ListNode*)malloc(sizeof(ListNode));node->…...

leetcode92:反转链表||
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left < right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。 示例 1: 输入:head [1,2,3,4,5], left 2, right 4 输出:[1,4,3,2…...

arkUI:遍历数据数组动态渲染(forEach)
arkUI:遍历数据数组动态渲染(forEach) 1 主要内容说明2 相关内容2.1 ForEach 的基本语法2.2 简单遍历数组2.2 多维数组遍历2.4 使用唯一键2.5 源码1的相关说明2.5.1 源码1 (遍历数据数组动态渲染)2.5.2 源码1运行效果 …...

js中import引入一个export值可以被修改。vue,react
import引入的数据实际就是数据本身。 如果导出的是一个对象,该对象引入后被更改了,则会影响其他文件引入此对象 解释示例: // resources.js const obj {} export {obj} 当在a.js中import引入一个空对象obj,并且新增一个属性ob…...

PDF24:多功能 PDF 工具使用指南
PDF24:多功能 PDF 工具使用指南 在日常工作和学习中,PDF 是一种常见且重要的文档格式。无论是查看、编辑、合并,还是转换 PDF 文件,能够快速高效地处理 PDF 文档对于提高工作效率至关重要。PDF24 是一款免费、功能全面的 PDF 工具…...

域名解析线路类型有哪几种
在网络世界中,域名解析是将域名转换为IP地址的关键环节,而域名解析线路类型的不同则为域名解析提供了多样化的策略,以满足不同用户和网络环境的需求。以下是几种常见的域名解析线路类型。 电信线路 电信线路解析主要是针对中国电信网络用户…...

Spring资源加载模块,原来XML就这,活该被注解踩在脚下 手写Spring第六篇了
这一篇让我想起来学习 Spring 的时,被 XML 支配的恐惧。明明是写Java,为啥要搞个XML呢?大佬们永远不知道,我认为最难的是 XML 头,但凡 Spring 用 JSON来做配置文件,Java 界都有可能再诞生一个扛把子。 <…...

[运维][Nginx]Nginx学习(2/5)-Nginx高级
Nginx服务器基础配置实例 前面我们已经对Nginx服务器默认配置文件的结构和涉及的基本指令做了详细的阐述。通过这些指令的合理配置,我们就可以让一台Nginx服务器正常工作,并且提供基本的web服务器功能。 接下来我们将通过一个比较完整和最简单的基础配…...

【快捷入门笔记】mysql基本操作大全-SQL数据库
SQL数据库 一、创建数据库 – 创建一个新数据库 fang_fang CREATE DATABASE fang_fang;– 显示所有数据库以确认创建 SHOW DATABASES;– 使用新数据库fang_fang USE fang_fang;– 检查我们正在使用哪个数据库 SELECT DATABASE();二、 删除数据库 –当你确定数据库存在并…...

【LeetCode】【算法】15. 三数之和
LeetCode 15. 三数之和 题目描述 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请你返回所有和为 0 且不重复的三元组。 注意:答案中不…...

传输协议设计与牧村摆动(Makimoto‘s Wave)
有一条活鱼和一条死鱼,你准备怎么做,你会将活鱼红烧或将死鱼清蒸吗?好的食材只需要最简单的烹饪,不好的食材才需要花活儿。 我此前的文字几乎都在阐述一个观点,广域网就是那条死鱼,数据中心则是那条活鱼。…...

JMeter进阶篇
目录 上篇导航: 总目录: 一、逻辑控制器: 1.逻辑控制器和关联: 2.if逻辑控制器: 3.forEach控制器: 4.循环控制器: 二、关联: 1.xpath: 2.正则表达式提取器&…...
--介绍)
LabVIEW编程基础教学(一)--介绍
LabVIEW(Laboratory Virtual Instrument Engineering Workbench)是一种基于图形化编程的开发环境,专为工程应用、测试、测量、控制系统等设计。与传统的文本编程语言不同,LabVIEW 使用图形化的方式通过“数据流”模型来表示程序逻…...

HVV蓝队基础
免责声明 学习视频来自B 站up主泷羽sec,如涉及侵权马上删除文章。 笔记的只是方便各位师傅学习知识,以下代码、网站只涉及学习内容,其他的都与本人无关,切莫逾越法律红线,否则后果自负。 企业网络架构 企业技术和信…...

[运维][Nginx]Nginx学习(1/5)--Nginx基础
Nginx简介 背景介绍 Nginx一个具有高性能的【HTTP】和【反向代理】的【WEB服务器】,同时也是一个【POP3/SMTP/IMAP代理服务器】,是由伊戈尔赛索耶夫(俄罗斯人)使用C语言编写的,Nginx的第一个版本是2004年10月4号发布的0.1.0版本。另外值得一…...

创客节小学组C++模拟题
来源:加码未来2024年深圳罗湖区创客节模拟题(小学组) 第一题 题目描述 给你n个数,找出出现次数超过一半的数。题目保证这样的数一定存在。 输入格式 第一行一个整数n,(n<=1000) 第二行n个整数(<1000000) 输出格式 输出一个整数 样例输入 5 1 2 3 3 3 样例输…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...

Python环境安装与虚拟环境配置详解
本文档旨在为Python开发者提供一站式的环境安装与虚拟环境配置指南,适用于Windows、macOS和Linux系统。无论你是初学者还是有经验的开发者,都能在此找到适合自己的环境搭建方法和常见问题的解决方案。 快速开始 一分钟快速安装与虚拟环境配置 # macOS/…...
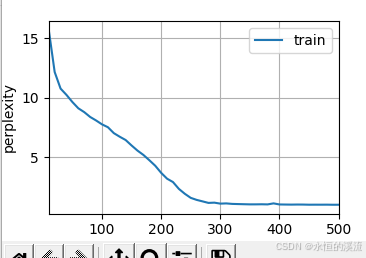
李沐--动手学深度学习--GRU
1.GRU从零开始实现 #9.1.2GRU从零开始实现 import torch from torch import nn from d2l import torch as d2l#首先读取 8.5节中使用的时间机器数据集 batch_size,num_steps 32,35 train_iter,vocab d2l.load_data_time_machine(batch_size,num_steps) #初始化模型参数 def …...

比特币:固若金汤的数字堡垒与它的四道防线
第一道防线:机密信函——无法破解的哈希加密 将每一笔比特币交易比作一封在堡垒内部传递的机密信函。 解释“哈希”(Hashing)就是一种军事级的加密术(SHA-256),能将信函内容(交易细节…...

WinUI3开发_使用mica效果
简介 Mica(云母)是Windows10/11上的一种现代化效果,是Windows10/11上所使用的Fluent Design(设计语言)里的一个效果,Windows10/11上所使用的Fluent Design皆旨在于打造一个人类、通用和真正感觉与 Windows 一样的设计。 WinUI3就是Windows10/11上的一个…...
