元器件封装
元器件封装类型
- 为什么越来越多用贴片元件,而不是插件元件
为什么越来越多用贴片元件,而不是插件元件
1.体积小、质量小、容易保存和运输;
2.容易焊接和拆卸。抗震效果好。
贴片元件不用过孔,用锡少。直插元件最麻烦的就是拆卸,在两层或更多层的PCB上拆卸时,哪怕只有两个引脚,将其拆下来都不容易,而且容易损坏电路板。拆卸贴片元件则容易且不容易损坏电路板。拆卸直插元件的主要工具是吸锡器(或者用惯性砸电路板),自动吸锡器价格昂贵,并且不易于保养,很容易损坏,且会产生气孔堵塞等问题。贴片元件是通过机器放置在PCB焊盘上,而直插元件一般依赖于人工放料。所以大批量生产时,贴片元件的效率会远高于直插元件。直插元件往往在焊接之后还需要额外“剪引脚”,当产量非常大时,会影响生产效率。
3.高频特性更好,减少了电磁和射频干扰。
由于贴片元件体积小、并不需要过孔,从而减小了杂散电场和杂散磁场。这在高频模拟电路和高速数字电路中十分重要。

电阻的寄生参数主要是并联的杂散电容Cp和引线导致的寄生电感Lp
直插电阻的引脚是“金属丝”形式,金属丝越长,则寄生电感越大。直插电阻的引脚长度不可能太短。
原因:1.引脚最短也一定要大于电阻横截面积的半径;2.直插电阻的引脚需要穿过PCB;3.一般弯折电阻引脚进行安装时,需要留一段距离避免电阻体受力,导致电阻损坏。
相比之下,表贴电阻的引脚就非常短,所以表贴电阻的寄生电感也小。
在具有电阻、电容和电感的电路中,对电路中电流起阻碍作用的是阻抗。
阻抗常用Z来表示,是一个复数,实部称为电阻,虚部称为电抗。其中,电容在电路中对直流电所起的阻碍作用称为容抗,电感在电路中对交流电所起的阻碍作用称为感抗,电容和电感在电路中对交流电所起的阻碍作用称为电抗。阻抗的单位是Ω。
阻抗是元器件对电路对周期的交流信号的总的反作用。理想电阻是阻抗的实部,寄生电感和寄生电容就是阻抗的虚部。
真实世界的电阻是由理想电阻加上寄生电容和寄生电感形成的。
简单地看,可以先把寄生的并联电容省略,即一个理想电阻串联一个理想电感。当串联一个寄生电感之后,则相当于阻抗增加了一个虚部。由于电感的特性是通直流,阻交流,因此相当于高频的阻抗上升。
阻抗在直角坐标系中用Z=R+jX。那么在极坐标系中,阻抗可以用幅度和相位表示。
直角坐标系中的实部和虚部可以通过数字换算成极坐标系中的幅度和相位。
阻抗Z=R+jwL
那么,对Z求模的结果
就是某个频率点的阻抗大小(这里没有把并联的电容那一条路算上),可以在复平面表示一个阻抗。
我们在讨论一些电路时,往往需要知道电路在各个频率点的阻抗绝对值,如高速数字电路的信号完整性分析、滤波器设计等。
所以我们一般会绘制一个阻抗和频率的函数曲线,用于描述阻抗特性。
选择一个10Ohm电阻,并设置寄生电容为0.2pF,寄生电感为10nH或20nH的电路,其阻抗特性曲线如下:

复阻抗平面表示一个阻抗
实际电阻的阻抗特性曲线
4.贴片元件提高了电路的稳定性和可靠性
直插元件的抗震能力偏差,在一些高可靠性的场景,需要对直插元件的引脚点上加固胶。
表贴元件因为体积小、质量小,在相同的参数情况下,震动的能量小,震动带来的对引脚的冲击能力就小。表贴元件的引脚不是直插元件的金属丝形式,而是大面积金属面与PCB焊盘焊接在一起。所以,表贴元件的引脚时刚性的,抗震能力更强。
但是贴片电阻也有缺点:容易虚焊、功率受限、容易积灰影响性能。但随着制造工艺和贴片焊接工艺的不断改进,贴片电阻的劣势在不断减小。
相关文章:

元器件封装
元器件封装类型 为什么越来越多用贴片元件,而不是插件元件 为什么越来越多用贴片元件,而不是插件元件 1.体积小、质量小、容易保存和运输; 2.容易焊接和拆卸。抗震效果好。 贴片元件不用过孔,用锡少。直插元件最麻烦的就是拆卸&a…...

状态空间方程离散化(Matlab符号函数)卡尔曼
// 卡尔曼滤波(4):扩展卡尔曼滤波 - 知乎 // // matlab 连续系统状态空间表达式的离散化&状态转移矩阵求解_matlab状态方程离散化-CSDN博客 // // // %https://blog.csdn.net/weixin_44051006/article/details/107007916 clear all; clc; syms R1 R2 C1 C…...

软件设计师-计算机网络
OSI网络模型 物理层,提供原始物理通路。数据交换的单位是二进制,bit,比特流,设备有中继器,集线器数据连输层,把原始不可靠的物理层链接变成无差错的数据通道,并解决多用户竞争问题。传送单位是帧ÿ…...
SpringBoot操作Elasticsearch
SpringBoot操作Elasticsearch SpringData框架简化Java代码连接ES的过程 官网:https://spring.io/projects/spring-data/ 以上列表中都是Spring Data支持连接的数据源 添加依赖 已经添加过了 <!--添加SpringDataES的依赖--><dependency><groupId&…...

阿里云aliyun gradle安装包下载地址
阿里云 查找你要下载的安装包 macports-distfiles-gradle安装包下载_开源镜像站-阿里云 https://mirrors.aliyun.com/macports/distfiles/gradle/gradle-8.9-bin.zip 腾讯 https://mirrors.cloud.tencent.com/gradle/ https://mirrors.cloud.tencent.com/gradle/ https…...

【设计模式】创建型设计模式-工厂模式的实现
工厂模式实现 定义例子UML类图理解Java代码实现总结 定义 工厂方法模式定义了一个接口用于创建对象,该模式由子类决定实例化哪个工厂类。该模式把类的实例化推迟到了子类。 例子 通过一个公共的类方法来管理画图对象的创建。 UML类图理解 Java代码实现 定义接口…...

【分布式】CAP理论
CAP定理的核心要点: CAP定理指出,任何一个分布式系统在面对网络分区(Partition)的情况下,最多只能同时满足以下三个特性中的两个: 一致性(Consistency): 所有节点在同一…...

市域社会治理现代化解决方案-2
1. 社会治理现代化背景 市域社会治理现代化旨在通过制度化、科学化、规范化、程序化和精细化的治理体系,实现社会治理能力的提升。该方案强调市一级的统筹协调和资源技术优势,以有效应对新型社会矛盾和风险挑战。 2. 社会治理面临的问题 当前社会治理在实践中存在诸多问题…...

谷歌浏览器的自动翻译功能如何开启
在当今全球化的网络环境中,能够流畅地浏览不同语言的网页是至关重要的。谷歌浏览器(Google Chrome)提供了一项强大的自动翻译功能,可以帮助用户轻松跨越语言障碍。本文将详细介绍如何开启和使用谷歌浏览器的自动翻译功能ÿ…...

Linux设置socks代理
公司里绝大多数主机已经禁止外网访问,仅保留一台主机设置socks作为代理服务器。如下为对socks这一概念的学习整理 什么是socks 是一种OSI模型下会话层的协议,位于表示层与传输层之间,作用是: exchanges network packets between…...

【ACM出版】第四届信号处理与通信技术国际学术会议(SPCT 2024)
& 第四届信号处理与通信技术国际学术会议(SPCT 2024) 2024 4th International Conference on Signal Processing and Communication Technology 2024年12月27-29日 中国深圳 www.icspct.com 第四届信号处理与通信技术国际学术会议&#x…...

蓝队技术学习
声明: 学习视频来自B站UP主 泷羽sec,如涉及侵权马上删除文 章。本文只涉及学习内容,其他的都与本人无关,切莫逾越法律红线, 否则后果自负 蓝队技术基础 1.企业网络架构:企业技术和信息团队的管理架构因企业而异。 CIO(Chief Informa…...
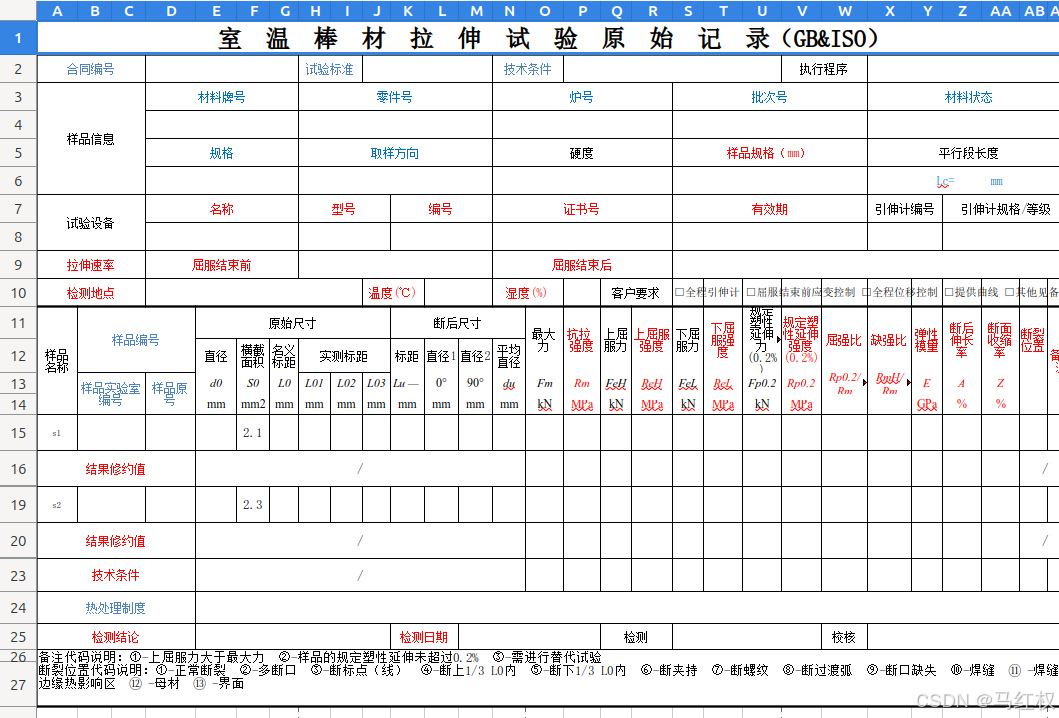
openpyxl处理Excel模板,带格式拷贝行和数据填入
本文中用openpyxl操作Excell 模板,进行行拷贝和数据填充. 主要涉及单元格格式的拷贝,合并单元格的拷贝,行高和列宽的处理. 将模板表格分为三部分,头部,中间循环填充部分,尾部.模板参数中设置头部高度,循环部分高度,剩余为尾部. 拷贝时先拷贝填充头部 ,然后根据数据循环拷贝填…...

无法在带有 WHM/cPanel 的 Ubuntu 22.04 服务器上安装 PHP 7.x – 缺少软件包
问题 正在使用Ubuntu 22.04设置服务器,并使用WHM/cPanel管理多个帐户和配置。我的目标是在服务器上安装 PHP 7.4(或更早的版本,如 PHP 7.3),因为我的一些应用程序与 PHP 8.x 不兼容。问题是,每当我尝试安装…...

数据结构-递归函数的调用栈过程
这道题考察的是递归函数的调用栈过程。 逐步分析程序的执行过程: main() 函数首先被调用,此时栈底是 main() 的信息。main() 函数调用 S(1),此时 S(1) 的信息被压入栈中,位于 main() 之上。S(1) 函数内部调用 S(0),因…...

在 WPF 中,如何实现数据的双向绑定?
在 WPF 中,数据绑定是一个非常重要的特性,它允许 UI 与数据源之间自动同步。双向绑定是一种常见的绑定方式,当数据源更新时,UI 会自动更新;同样,当 UI 中的元素(如文本框)发生改变时…...

pyinstaller 打包 playwright -- 如何将浏览器打包到程序中
start 最近玩了玩 playwright,记录一下遇到的问题。 1. 如何在 python 中使用 安装 pip install playwright安装浏览器驱动 playwright install查看浏览器驱动安装的位置 playwright install --dry-run2. 如何将浏览器打包的程序中 先找到我们使用 pip 安装…...

vue系列=状态管理=Pinia使用
1、Pinia基本概念 1、Pinia向外暴露了几个重要的函数,分别是createPinia、defineStore和storeToRefs 2、pinia有五个核心管理概念: store、store、getters、action、plugins 2、Pinia基本使用 1、安装过程 1、安装pinia插件:npm install pini…...

[HarmonyOS]简单说一下鸿蒙架构
鸿蒙操作系统(HarmonyOS)是由华为公司开发的一款面向全场景的操作分布式系统。它旨在提供一个统一的操作系统平台,支持多种设备,包括智能手机、平板电脑、智能电视、可穿戴设备、智能家居等。鸿蒙架构的设计目标是实现设备之间的无…...

【Python TensorFlow】进阶指南(续篇一)
在前两篇文章中,我们介绍了TensorFlow的基础知识及其在实际应用中的初步使用,并探讨了更高级的功能和技术细节。本篇将继续深入探讨TensorFlow的高级应用,包括但不限于模型压缩、模型融合、迁移学习、强化学习等领域,帮助读者进一…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
