概率论中的PMF、PDF和CDF
在概率论中,PMF(概率质量函数)、PDF(概率密度函数)和CDF(累积分布函数)是描述随机变量分布的三个重要概念。它们分别用于不同类型的随机变量,并帮助我们理解随机事件的概率特性。本文将详细介绍这些概念及其之间的关系。
PMF: Probability Mass Function 概率质量函数
PDF: Probability Density Function 概率密度函数
CDF: Cumulative Distribution Function 累积分布函数
1. PMF(概率质量函数)
PMF用于离散型随机变量。离散型随机变量的取值是有限的或可数的,即它的可能值是可以一一列举出来的,比如掷骰子时的点数(1到6)。
PMF的定义是:对于一个离散型随机变量 X X X,PMF P ( X = x ) P(X = x) P(X=x) 表示随机变量 X X X 取值为 x x x 的概率。具体来说,PMF必须满足以下条件:
-
P ( X = x ) ≥ 0 P(X = x) \geq 0 P(X=x)≥0 对于所有 x x x。
-
所有可能的值 x x x 的概率之和必须为1,即
∑ x P ( X = x ) = 1 \sum_{x} P(X = x) = 1 x∑P(X=x)=1
例如,在掷一个公平的六面骰子的情况下,PMF为:
P ( X = x ) = 1 6 , x = 1 , 2 , 3 , 4 , 5 , 6 P(X = x) = \frac{1}{6}, \quad x = 1, 2, 3, 4, 5, 6 P(X=x)=61,x=1,2,3,4,5,6
2. PDF(概率密度函数)
PDF用于连续型随机变量。与离散型随机变量不同,连续型随机变量的取值是一个区间上的实数(例如身高、体重、时间等)。对于连续型随机变量 X X X,我们无法直接计算 P ( X = x ) P(X = x) P(X=x),因为在任何单一的点上,连续随机变量的概率为0。相反,我们用概率密度来描述其概率分布。
PDF的定义是:一个随机变量 X X X 的概率密度函数 f X ( x ) f_X(x) fX(x) 满足以下条件:
-
f X ( x ) ≥ 0 f_X(x) \geq 0 fX(x)≥0 对于所有 x x x。
-
随机变量 X X X 取某个区间 [ a , b ] [a, b] [a,b] 内的值的概率可以通过积分计算:
P ( a ≤ X ≤ b ) = ∫ a b f X ( x ) d x P(a \leq X \leq b) = \int_a^b f_X(x) \, dx P(a≤X≤b)=∫abfX(x)dx
此外,PDF的整体积分为1,即:
∫ − ∞ ∞ f X ( x ) d x = 1 \int_{-\infty}^{\infty} f_X(x) \, dx = 1 ∫−∞∞fX(x)dx=1
常见的PDF包括正态分布、均匀分布、指数分布等。
例如,标准正态分布的PDF为:
f X ( x ) = 1 2 π e − x 2 / 2 f_X(x) = \frac{1}{\sqrt{2\pi}} e^{-x^2 / 2} fX(x)=2π1e−x2/2
表示一个标准正态随机变量的概率密度。
3. CDF(累积分布函数)
CDF是描述随机变量小于或等于某个特定值的概率的函数。对于任意的随机变量 X X X(无论是离散的还是连续的),其累积分布函数 F X ( x ) F_X(x) FX(x) 定义为:
F X ( x ) = P ( X ≤ x ) F_X(x) = P(X \leq x) FX(x)=P(X≤x)
CDF具有以下两个主要性质:
- 单调性:累积分布函数是单调非降的,即 F X ( x 1 ) ≤ F X ( x 2 ) F_X(x_1) \leq F_X(x_2) FX(x1)≤FX(x2) 对于 x 1 ≤ x 2 x_1 \leq x_2 x1≤x2 成立。
- 极限:当 x → − ∞ x \to -\infty x→−∞ 时, F X ( x ) → 0 F_X(x) \to 0 FX(x)→0;当 x → + ∞ x \to +\infty x→+∞ 时, F X ( x ) → 1 F_X(x) \to 1 FX(x)→1。
CDF可以通过PDF或PMF推导得出:
-
对于离散型随机变量,CDF是PMF的累加:
F X ( x ) = ∑ x ′ ≤ x P ( X = x ′ ) F_X(x) = \sum_{x' \leq x} P(X = x') FX(x)=x′≤x∑P(X=x′) -
对于连续型随机变量,CDF是PDF的积分:
F X ( x ) = ∫ − ∞ x f X ( t ) d t F_X(x) = \int_{-\infty}^{x} f_X(t) \, dt FX(x)=∫−∞xfX(t)dt
4. PMF, PDF, CDF 之间的关系
-
对于离散型随机变量,PMF和CDF有直接的关系。CDF是PMF的累加,表示随机变量小于等于某个值的概率。
-
对于连续型随机变量,PDF和CDF通过积分和导数相关联。具体地,CDF是PDF的积分,而PDF是CDF的导数。即:
F X ( x ) = ∫ − ∞ x f X ( t ) d t , f X ( x ) = d d x F X ( x ) F_X(x) = \int_{-\infty}^{x} f_X(t) \, dt, \quad f_X(x) = \frac{d}{dx} F_X(x) FX(x)=∫−∞xfX(t)dt,fX(x)=dxdFX(x)
相关文章:

概率论中的PMF、PDF和CDF
在概率论中,PMF(概率质量函数)、PDF(概率密度函数)和CDF(累积分布函数)是描述随机变量分布的三个重要概念。它们分别用于不同类型的随机变量,并帮助我们理解随机事件的概率特性。本文…...

Vue 简单入手
前端工程化(Front-end Engineering)指的是在前端开发中,通过一系列工具、流程和规范的整合,以提高开发效率、代码质量和可维护性的一种技术和实践方法。其核心目的是使得前端开发变得更高效、可扩展和可维护。 文章目录 一、Vue 项…...

Github配置ssh key原理及操作步骤
文章目录 配置SSH第一步:检查本地主机是否已经存在ssh key第二步:生成ssh key第三步:获取ssh key公钥内容第四步:Github账号上添加公钥第五步:验证是否设置成功验证原理 往github上push项目的时候,如果走ht…...

大循环引起CPU负载过高
一、问题背景 环境:jdk1.8 tomcat7 在一次发布时,cpu出现负载过高,其负载突破200%,并且响应时间也大幅度超时。 二、问题分析 【1】发布前做过压测,并没有发现cpu异常升高的现象,所以其可能与生产环境的请…...
[Java]微服务治理
注册中心原理 注册中心可以统一管理项目中的所有服务 服务治理中的三个角色分别是什么? 服务提供者: 暴露服务接口,供其它服务调用服务消费者: 调用其它服务提供的接口注册中心: 记录并监控微服务各实例状态,推送服务变更信息 消费者如何知道提供者的…...

深入解析C语言中的extern关键字:语法、工作原理与高级应用技巧
引言 在C语言中,extern 关键字是一个强大的工具,用于声明外部变量和函数,使得这些变量和函数可以在多个源文件之间共享。理解 extern 的工作原理和最佳实践对于编写模块化、可维护的代码至关重要。本文将深入探讨 extern 关键字的各个方面&a…...

元器件封装
元器件封装类型 为什么越来越多用贴片元件,而不是插件元件 为什么越来越多用贴片元件,而不是插件元件 1.体积小、质量小、容易保存和运输; 2.容易焊接和拆卸。抗震效果好。 贴片元件不用过孔,用锡少。直插元件最麻烦的就是拆卸&a…...

状态空间方程离散化(Matlab符号函数)卡尔曼
// 卡尔曼滤波(4):扩展卡尔曼滤波 - 知乎 // // matlab 连续系统状态空间表达式的离散化&状态转移矩阵求解_matlab状态方程离散化-CSDN博客 // // // %https://blog.csdn.net/weixin_44051006/article/details/107007916 clear all; clc; syms R1 R2 C1 C…...

软件设计师-计算机网络
OSI网络模型 物理层,提供原始物理通路。数据交换的单位是二进制,bit,比特流,设备有中继器,集线器数据连输层,把原始不可靠的物理层链接变成无差错的数据通道,并解决多用户竞争问题。传送单位是帧ÿ…...
SpringBoot操作Elasticsearch
SpringBoot操作Elasticsearch SpringData框架简化Java代码连接ES的过程 官网:https://spring.io/projects/spring-data/ 以上列表中都是Spring Data支持连接的数据源 添加依赖 已经添加过了 <!--添加SpringDataES的依赖--><dependency><groupId&…...

阿里云aliyun gradle安装包下载地址
阿里云 查找你要下载的安装包 macports-distfiles-gradle安装包下载_开源镜像站-阿里云 https://mirrors.aliyun.com/macports/distfiles/gradle/gradle-8.9-bin.zip 腾讯 https://mirrors.cloud.tencent.com/gradle/ https://mirrors.cloud.tencent.com/gradle/ https…...

【设计模式】创建型设计模式-工厂模式的实现
工厂模式实现 定义例子UML类图理解Java代码实现总结 定义 工厂方法模式定义了一个接口用于创建对象,该模式由子类决定实例化哪个工厂类。该模式把类的实例化推迟到了子类。 例子 通过一个公共的类方法来管理画图对象的创建。 UML类图理解 Java代码实现 定义接口…...

【分布式】CAP理论
CAP定理的核心要点: CAP定理指出,任何一个分布式系统在面对网络分区(Partition)的情况下,最多只能同时满足以下三个特性中的两个: 一致性(Consistency): 所有节点在同一…...

市域社会治理现代化解决方案-2
1. 社会治理现代化背景 市域社会治理现代化旨在通过制度化、科学化、规范化、程序化和精细化的治理体系,实现社会治理能力的提升。该方案强调市一级的统筹协调和资源技术优势,以有效应对新型社会矛盾和风险挑战。 2. 社会治理面临的问题 当前社会治理在实践中存在诸多问题…...

谷歌浏览器的自动翻译功能如何开启
在当今全球化的网络环境中,能够流畅地浏览不同语言的网页是至关重要的。谷歌浏览器(Google Chrome)提供了一项强大的自动翻译功能,可以帮助用户轻松跨越语言障碍。本文将详细介绍如何开启和使用谷歌浏览器的自动翻译功能ÿ…...

Linux设置socks代理
公司里绝大多数主机已经禁止外网访问,仅保留一台主机设置socks作为代理服务器。如下为对socks这一概念的学习整理 什么是socks 是一种OSI模型下会话层的协议,位于表示层与传输层之间,作用是: exchanges network packets between…...

【ACM出版】第四届信号处理与通信技术国际学术会议(SPCT 2024)
& 第四届信号处理与通信技术国际学术会议(SPCT 2024) 2024 4th International Conference on Signal Processing and Communication Technology 2024年12月27-29日 中国深圳 www.icspct.com 第四届信号处理与通信技术国际学术会议&#x…...

蓝队技术学习
声明: 学习视频来自B站UP主 泷羽sec,如涉及侵权马上删除文 章。本文只涉及学习内容,其他的都与本人无关,切莫逾越法律红线, 否则后果自负 蓝队技术基础 1.企业网络架构:企业技术和信息团队的管理架构因企业而异。 CIO(Chief Informa…...
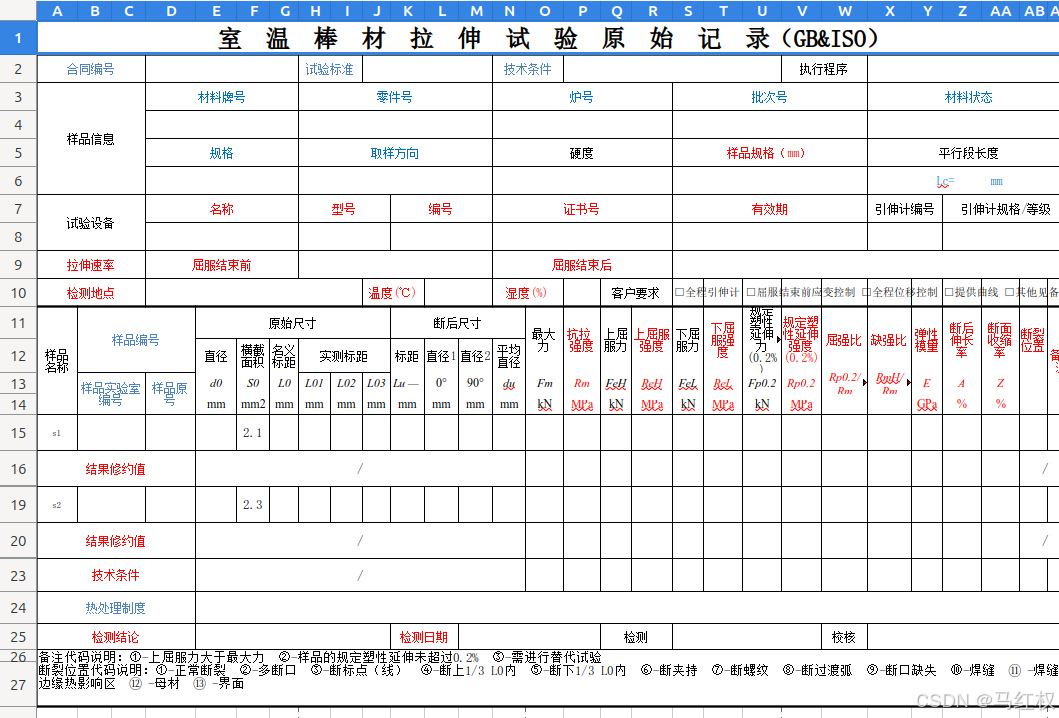
openpyxl处理Excel模板,带格式拷贝行和数据填入
本文中用openpyxl操作Excell 模板,进行行拷贝和数据填充. 主要涉及单元格格式的拷贝,合并单元格的拷贝,行高和列宽的处理. 将模板表格分为三部分,头部,中间循环填充部分,尾部.模板参数中设置头部高度,循环部分高度,剩余为尾部. 拷贝时先拷贝填充头部 ,然后根据数据循环拷贝填…...

无法在带有 WHM/cPanel 的 Ubuntu 22.04 服务器上安装 PHP 7.x – 缺少软件包
问题 正在使用Ubuntu 22.04设置服务器,并使用WHM/cPanel管理多个帐户和配置。我的目标是在服务器上安装 PHP 7.4(或更早的版本,如 PHP 7.3),因为我的一些应用程序与 PHP 8.x 不兼容。问题是,每当我尝试安装…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
