matlab建模入门指导

        本文以水池中鸡蛋温度随时间的变化为切入点，对其进行数学建模并进行MATLAB求解，以更为通俗地进行数学建模问题入门指导。

一、问题简述

    一个煮熟的鸡蛋有98摄氏度，将它放在18摄氏度的水池中，五分钟后鸡蛋的温度为38摄氏度，假定没有感到水变热，问鸡蛋的温度是怎样随着时间进行变化的，达到20摄氏度又需多长时间？

二、牛顿冷却定律

        牛顿冷却定律（Newton's Law of Cooling）是热传递领域的一个基本定律，用于描述物体温度随时间变化的规律。该定律指出，物体温度变化的速率与其自身温度和周围环境温度之间的差值成正比。这个定律在工程、物理和日常生活中都有广泛的应用，例如在烹饪、制冷、医学和环境科学等领域。

        牛顿冷却定律可以用以下数学公式表示：

       

        其中T 是物体在时间 t 时的温度；Ta​ 是周围环境的温度；k 是一个正的比例常数，称为冷却系数；dtdT​ 是物体温度随时间变化的速率。

1. 温度差T−Ta​ 表示物体与环境之间的温度差。当物体的温度高于环境温度时，T−Ta​ 为正，物体失去热量；当物体的温度低于环境温度时，T−Ta​ 为负，物体吸收热量。

2. 冷却系数：k 是一个正的比例常数，它取决于物体的材料、形状、大小以及周围环境的条件。k 越大，物体的温度变化速率越快。

3. 微分方程：这个方程是一个一阶线性微分方程，可以通过分离变量法或使用积分因子来求解。

        对于上述微分方程，我们可以求解得到物体温度随时间变化的函数：

     

        其中T0​ 是物体在t=0 时的初始温度。这个解表明，随着时间的推移，物体的温度会逐渐接近环境温度 a​。当 t 趋向于无穷大时，e−kt 趋向于 0，因此T(t) 趋向于Ta​。

        下面是一个使用MATLAB实现牛顿冷却定律的简单示例。这个示例将模拟一个物体从初始温度 T0​ 开始冷却到环境温度 Ta​ 的过程，并绘制温度随时间变化的曲线。

% 牛顿冷却定律的MATLAB实现% 参数设置
T0 = 100; % 初始温度，单位：摄氏度
Ta = 20;  % 环境温度，单位：摄氏度
k = 0.05; % 冷却系数
t_final = 100; % 最终时间，单位：分钟
dt = 0.1; % 时间步长，单位：分钟% 时间向量
t = 0:dt:t_final;% 初始化温度向量
T = zeros(size(t));
T(1) = T0;% 使用欧拉方法求解微分方程
for i = 1:length(t)-1dT = -k * (T(i) - Ta);T(i+1) = T(i) + dT * dt;
end% 绘制温度随时间变化的曲线
figure;
plot(t, T, 'LineWidth', 2);
xlabel('时间 (分钟)');
ylabel('温度 (摄氏度)');
title('牛顿冷却定律模拟');
grid on;

        运行这段代码后，你将看到一个温度随时间变化的曲线图，展示了物体从初始温度冷却到接近环境温度的过程。

三、数据分析

    牛顿冷却定律描述了物体温度随时间变化的过程，描述了物体与环境之间的温差与温度变化的速率之间的物理关系，根据逆向思维亦知该定律也适用于加热过程，其公式如下：

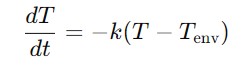
    其中T 为物体的温度，Tenv 为环境温度，k 为冷却常数，表示冷却速率，t 为时间。

    该方程表明，物体的温度变化速率与物体温度和环境温度之间的差异成正比。对该方程进行积分，可以得到物体温度随时间的变化关系：

    其中，T0 为物体的初始温度，T(t) 为时间 t 时物体的温度，k 为冷却常数。

    根据题意，鸡蛋初始温度为98°C，环境温度为18°C，经过5分钟后，鸡蛋的温度降至38°C。假设水池的温度变化可以忽略不计，即水池的温度保持稳定不变，则有条件归纳如下：

    带入求解可解k≈1.386/5=0.2772/min，联立T(t)=20摄氏度，可求解t≈3.689/0.277≈13.3min。

四、MATLAB求解

    为了模拟鸡蛋在水池中冷却过程并根据牛顿冷却定律计算降温所需的时间，我们可以用 MATLAB 编写代码进行数值计算和绘图，其代码如下：

cleark=5/(log(20)-log(80));c=log(80)*(-k);t=[0:0.5:20]+eps;for i=1:length(t)T(i)=exp((t(i)-c)./k)+18;endfigure,plot(T,t,'d-');xlabel('time');ylabel('temperture');

        运行之后可得到下图所示温度与时间的曲线图。

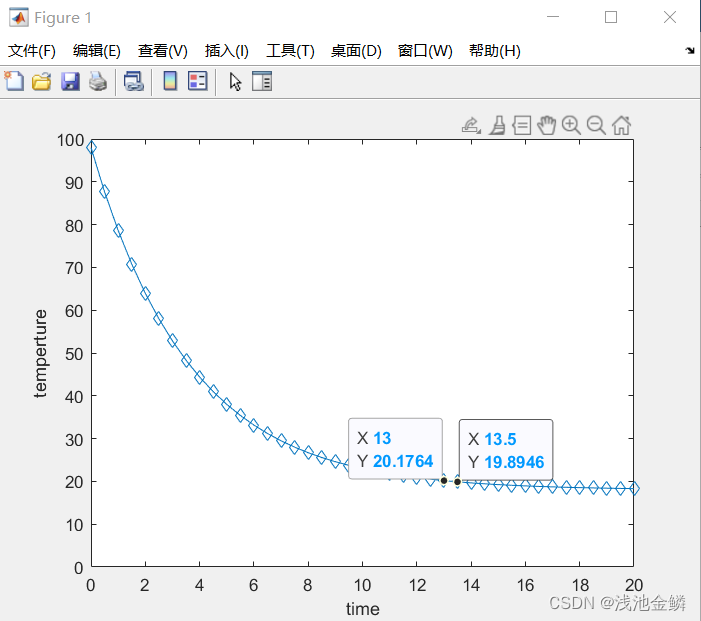
    如图所示，在13min时鸡蛋温度为20.1764摄氏度，在13.5min时鸡蛋温度为19.8964摄氏度，更为直观的展示了鸡蛋的温度是如何随着时间进行变化的。