Day62||prim算法精讲 |kruskal算法精讲

prim算法精讲

53. 寻宝（第七期模拟笔试）

题目描述

在世界的某个区域，有一些分散的神秘岛屿，每个岛屿上都有一种珍稀的资源或者宝藏。国王打算在这些岛屿上建公路，方便运输。

不同岛屿之间，路途距离不同，国王希望你可以规划建公路的方案，如何可以以最短的总公路距离将 所有岛屿联通起来（注意：这是一个无向图）。 

给定一张地图，其中包括了所有的岛屿，以及它们之间的距离。以最小化公路建设长度，确保可以链接到所有岛屿。

输入描述

第一行包含两个整数V 和 E，V代表顶点数，E代表边数 。顶点编号是从1到V。例如：V=2，一个有两个顶点，分别是1和2。

接下来共有 E 行，每行三个整数 v1，v2 和 val，v1 和 v2 为边的起点和终点，val代表边的权值。

输出描述

输出联通所有岛屿的最小路径总距离

输入示例

7 11
1 2 1
1 3 1
1 5 2
2 6 1
2 4 2
2 3 2
3 4 1
4 5 1
5 6 2
5 7 1
6 7 1

输出示例

6

提示信息

数据范围：
2 <= V <= 10000;
1 <= E <= 100000;
0 <= val <= 10000;

如下图，可见将所有的顶点都访问一遍，总距离最低是6.

  

 最小生成树的模板题。

最小生成树是所有节点的最小连通子图， 即：以最小的成本（边的权值）将图中所有节点链接到一起。

prim算法 是从节点的角度 采用贪心的策略 每次寻找距离 最小生成树最近的节点 并加入到最小生成树中。

prim算法核心就是三步，我称为prim三部曲

1. 第一步，选距离生成树最近节点
2. 第二步，最近节点加入生成树
3. 第三步，更新非生成树节点到生成树的距离（即更新minDist数组）

minDist数组 用来记录 每一个节点距离最小生成树的最近距离。

1.初始状态

minDist 数组 里的数值初始化为 最大数

2. 

1.选距离生成树最近节点，任取一点就可以

2.最近节点加入生成树

3.

更新非生成树节点到生成树的距离（即更新minDist数组）

接下来，我们要更新所有节点距离最小生成树的距离，如图：

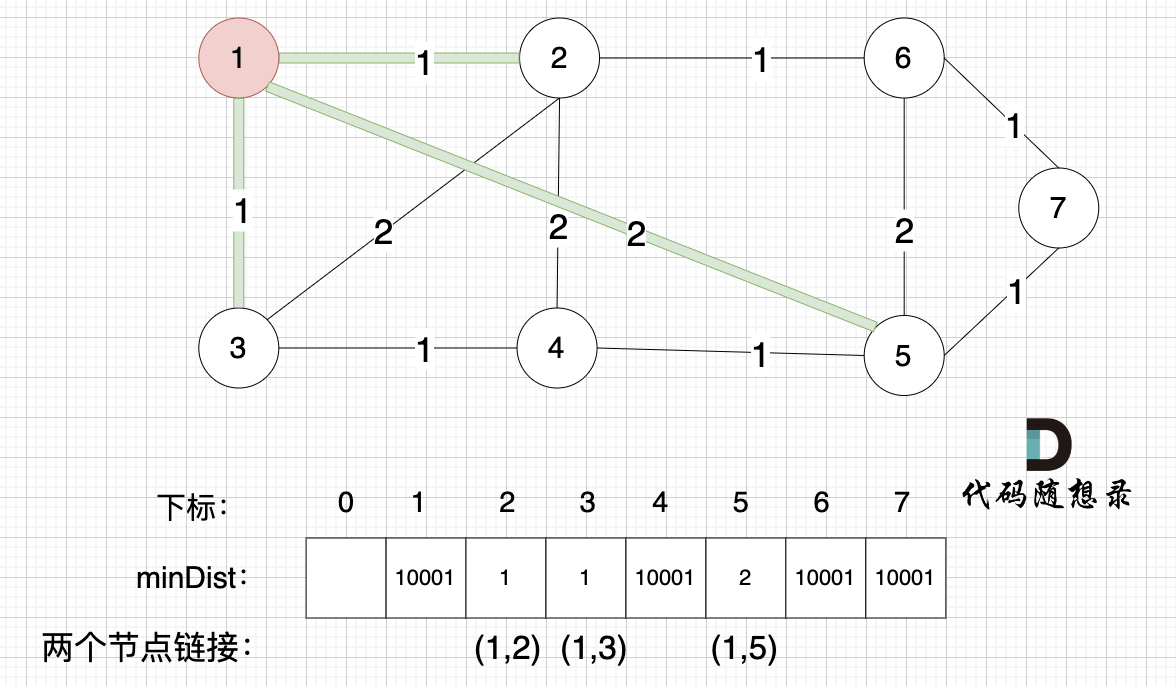
然后第二步选节点2或3都行，依据三部曲执行过程。不断更新mindist值

流程

选择节点2

 选择节点3

选择离最小生成树的最近节点4

选择5

选6

最后选7

最后，累加mindist的等于1的值，就是最小生成树的权重总和。

代码

邻接矩阵。节点对应的边的关系。

#include<iostream>
#include<vector>
#include<climits>
using namespace std;
int main()
{int v,e;//点和边的数量int x,y,k;//起点，终点，边的权重cin>>v>>e;//声明一个大小为 (v + 1) x (v + 1) 的二维向量 grid，用于存储图的邻接矩阵。初始值为10001，表示不存在的边或非常大的权值。vector<vector<int>>grid(v+1,vector<int>(v+1,10001));//读取边构建邻接矩阵while(e--){cin>>x>>y>>k;//因为图是无向的，所以两个方向的权重都设置为 k。grid[x][y]=k;grid[y][x]=k;}vector<int>minDist(v+1,10001);//用于存储每个节点到最小生成树的最小距离vector<int>isintree(v+1,false);//用于标记每个节点是否已经加入最小生成树，初始值为 false。//prim算法精华for(int i=1;i<v;i++)//循环 v - 1 次，因为最小生成树需要 v - 1 条边。{//第一步，选距离生成树最近的节点int cur=-1;int minVal=INT_MAX;for(int j=1;j<=v;j++)//1到v{//  选取最小生成树节点的条件：//  （1）不在最小生成树里//  （2）距离最小生成树最近的节点if(!isintree[j]&&minDist[j]<minVal){minVal=minDist[j];cur=j;//更新最近节点}}//第二步，把最近节点加入生成树中isintree[cur]=true;//第三步，更新mindist值// cur节点加入之后， 最小生成树加入了新的节点，那么所有节点到 最小生成树的距离（即minDist数组）需要更新一下// 由于cur节点是新加入到最小生成树，那么只需要关心与 cur 相连的 非生成树节点 的距离 是否比 原来 非生成树节点到生成树节点的距离更小了呢for(int i=1;i<=v;i++){// 更新的条件：// （1）节点是 非生成树里的节点// （2）与cur相连的某节点的权值 比 该某节点距离最小生成树的距离小if(!isintree[i]&&grid[cur][i]<minDist[i])minDist[i]=grid[cur][i];}}int result=0;//输出生成树权重for(int i=2;i<=v;i++){result+=minDist[i];}cout<<result<<endl;}

 

模拟运行结果

假设输入如下：

4 6
1 2 1
1 3 2
1 4 3
2 3 4
2 4 5
3 4 6

• 首先读取 v=4 和 e=6，初始化邻接矩阵 grid。

• 读取边并填充邻接矩阵：

  • 边 (1, 2, 1)，grid[1][2] = 1，grid[2][1] = 1
  • 边 (1, 3, 2)，grid[1][3] = 2，grid[3][1] = 2
  • 边 (1, 4, 3)，grid[1][4] = 3，grid[4][1] = 3
  • 边 (2, 3, 4)，grid[2][3] = 4，grid[3][2] = 4
  • 边 (2, 4, 5)，grid[2][4] = 5，grid[4][2] = 5
  • 边 (3, 4, 6)，grid[3][4] = 6，grid[4][3] = 6

• 初始化 minDist 和 isInTree。

• 运行 Prim 算法：

  • 第一次迭代：选择节点1，更新 minDist 为 [10001, 1, 2, 3]。
  • 第二次迭代：选择节点2，更新 minDist 为 [10001, 1, 2, 3]。
  • 第三次迭代：选择节点3，更新 minDist 为 [10001, 1, 2, 3]。

• 统计结果：

  • result = 1 + 2 + 3 = 6

最终输出：

6

 

 kruskal算法精讲

如上题，这里是另一种解法。

 Kruskal 是维护边的集合。

kruscal的思路：

• 边的权值排序，因为要优先选最小的边加入到生成树里
• 遍历排序后的边
  • 如果边首尾的两个节点在同一个集合，说明如果连上这条边图中会出现环
  • 如果边首尾的两个节点不在同一个集合，加入到最小生成树，并把两个节点加入同一个集合

开始从头遍历排序后的边。

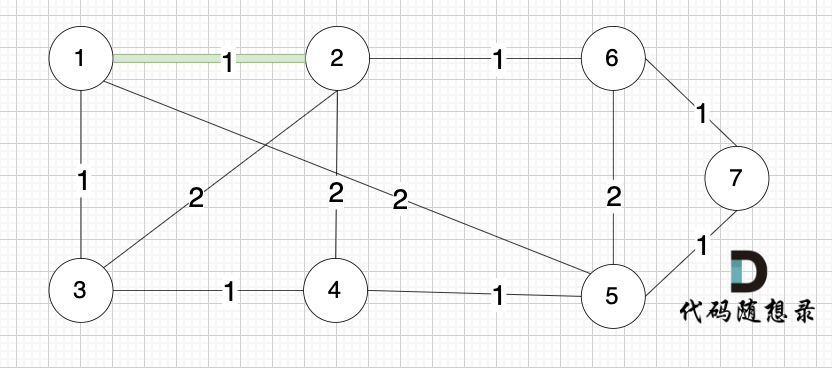
选边(1,2)，节点1 和 节点2 不在同一个集合，所以生成树可以添加边(1,2)，并将 节点1，节点2 放在同一个集合。

---

选边(4,5)，节点4 和 节点 5 不在同一个集合，生成树可以添加边(4,5) ，并将节点4，节点5 放到同一个集合。

大家判断两个节点是否在同一个集合，就看图中两个节点是否有绿色的粗线连着就行

---

（这里在强调一下，以下选边是按照上面排序好的边的数组来选择的）

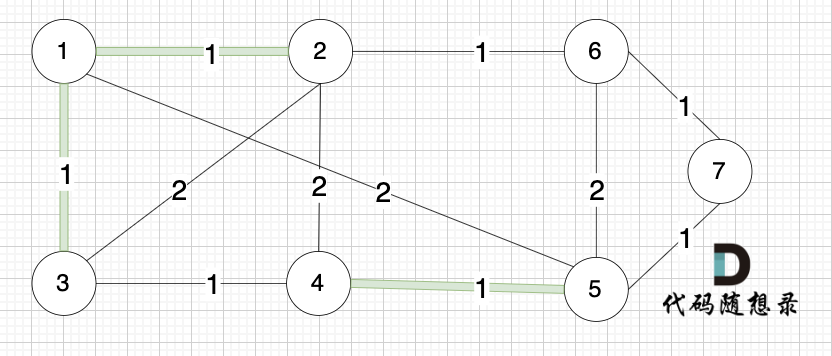
选边(1,3)，节点1 和 节点3 不在同一个集合，生成树添加边(1,3)，并将节点1，节点3 放到同一个集合。

---

选边(2,6)，节点2 和 节点6 不在同一个集合，生成树添加边(2,6)，并将节点2，节点6 放到同一个集合。

---

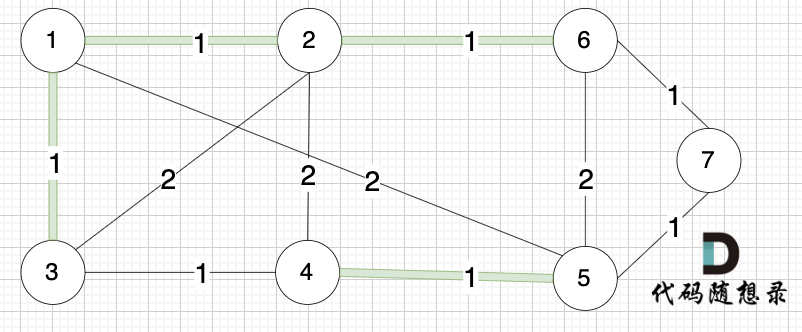
选边(3,4)，节点3 和 节点4 不在同一个集合，生成树添加边(3,4)，并将节点3，节点4 放到同一个集合。

---

选边(6,7)，节点6 和 节点7 不在同一个集合，生成树添加边(6,7)，并将 节点6，节点7 放到同一个集合。

---

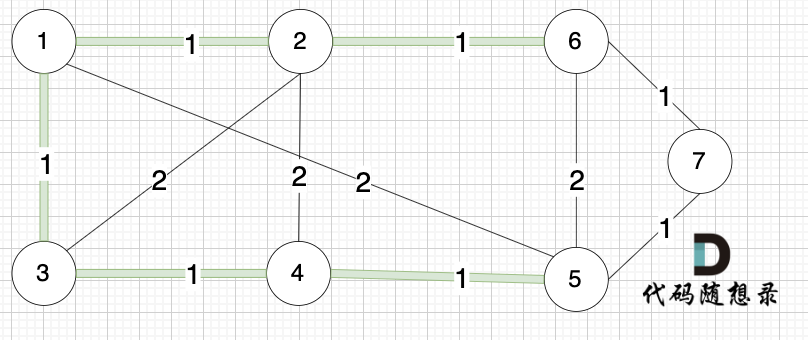
选边(5,7)，节点5 和 节点7 在同一个集合，不做计算。

选边(1,5)，两个节点在同一个集合，不做计算。

后面遍历 边(3,2)，(2,4)，(5,6) 同理，都因两个节点已经在同一集合，不做计算。

---

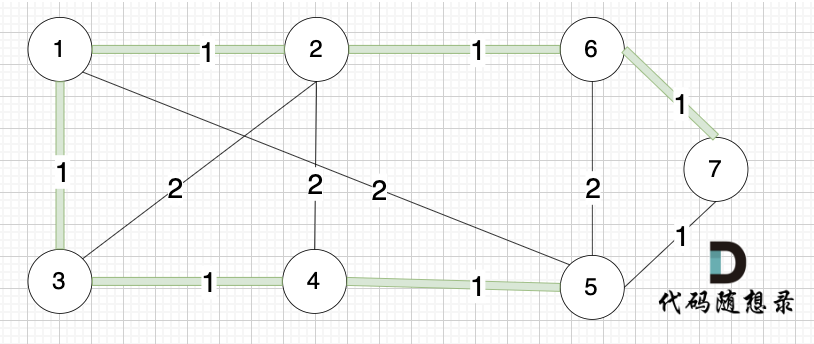
此时 我们就已经生成了一个最小生成树，即：

 

代码 

用到并查集。

功能：

• 将两个元素添加到一个集合中
• 判断两个元素在不在同一个集合

#include <iostream>
#include <vector>
#include <algorithm>using namespace std;// l,r为 边两边的节点，val为边的数值
struct Edge {int l, r, val;
};// 节点数量
int n = 10001;
// 并查集标记节点关系的数组
vector<int> father(n, -1); // 节点编号是从1开始的，n要大一些// 并查集初始化
void init() {for (int i = 0; i < n; ++i) {father[i] = i;}
}// 并查集的查找操作
int find(int u) {return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
}// 并查集的加入集合
void join(int u, int v) {u = find(u); // 寻找u的根v = find(v); // 寻找v的根if (u == v) return ; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回father[v] = u;
}int main() {int v, e;int v1, v2, val;vector<Edge> edges;int result_val = 0;cin >> v >> e;while (e--) {cin >> v1 >> v2 >> val;edges.push_back({v1, v2, val});}// 执行Kruskal算法// 按边的权值对边进行从小到大排序sort(edges.begin(), edges.end(), [](const Edge& a, const Edge& b) {return a.val < b.val;});// 并查集初始化init();// 从头开始遍历边for (Edge edge : edges) {// 并查集，搜出两个节点的祖先int x = find(edge.l);int y = find(edge.r);// 如果祖先不同，则不在同一个集合if (x != y) {result_val += edge.val; // 这条边可以作为生成树的边join(x, y); // 两个节点加入到同一个集合}}cout << result_val << endl;return 0;
}

模拟运行结果

假设输入如下：

4 6
1 2 1
1 3 2
1 4 3
2 3 4
2 4 5
3 4 6

• 首先读取 v=4 和 e=6，初始化 father 数组。

• 读取边并存储在 edges 中：

  • 边 (1, 2, 1)
  • 边 (1, 3, 2)
  • 边 (1, 4, 3)
  • 边 (2, 3, 4)
  • 边 (2, 4, 5)
  • 边 (3, 4, 6)

• 按边的权重从小到大排序：

  • 边 (1, 2, 1)
  • 边 (1, 3, 2)
  • 边 (1, 4, 3)
  • 边 (2, 3, 4)
  • 边 (2, 4, 5)
  • 边 (3, 4, 6)

• 初始化并查集。

• 遍历排序后的边：

  • 边 (1, 2, 1)：1 和 2 不在同一个集合，加入生成树，result_val = 1。
  • 边 (1, 3, 2)：1 和 3 不在同一个集合，加入生成树，result_val = 3。
  • 边 (1, 4, 3)：1 和 4 不在同一个集合，加入生成树，result_val = 6。
  • 边 (2, 3, 4)：2 和 3 在同一个集合，跳过。
  • 边 (2, 4, 5)：2 和 4 在同一个集合，跳过。
  • 边 (3, 4, 6)：3 和 4 在同一个集合，跳过。

• 最终输出：

  6