DAY24|回溯算法Part03|LeetCode:93.复原IP地址、78.子集、90.子集II
目录
LeetCode:93.复原IP地址
基本思路
C++代码
LeetCode:78.子集
基本思路
C++代码
LeetCode:90.子集II
基本思路
C++代码
通过used实现去重
通过set实现去重
不使用used和set版本
LeetCode:93.复原IP地址
力扣代码链接
文字讲解:LeetCode:93.复原IP地址
视频讲解:回溯算法如何分割字符串并判断是合法IP?

基本思路
首先应该意识到属于切割问题,而切割问题就是和之前做过的分割回文串是类似的,要通过回溯算法将所有的可能性搜索出来,抽象为树形结构可以表示为:

- 递归函数参数
需要定义一个全局变量vector<string> result用来存放符合条件的结果。
参数:startIndex一定是需要的,因为不能重复分割,记录下一层递归分割的起始位置。另外还需要一个变量pointNum,记录添加逗点的数量。
vector<string> result;// 记录结果
// startIndex: 搜索的起始位置,pointNum:添加逗点的数量
void backtracking(string& s, int startIndex, int pointNum)- 递归终止条件
本题明确要求只会分成4段,所以不能用切割线切到最后作为终止条件,而是分割的段数作为终止条件。pointNum表示逗点数量,pointNum为3说明字符串分成了4段了。然后验证一下第四段是否合法,如果合法就加入到结果集里。
if (pointNum == 3) { // 逗点数量为3时,分隔结束// 判断第四段子字符串是否合法,如果合法就放进result中if (isValid(s, startIndex, s.size() - 1)) {result.push_back(s);}return;
}- 单层搜索的逻辑
在for (int i = startIndex; i < s.size(); i++)循环中 [startIndex, i] 这个区间就是截取的子串,需要判断这个子串是否合法。如果合法就加上' . ',递归调用时,下一层递归的startIndex要从i+2开始(因为需要在字符串中加入了分隔符.),同时记录分割符的数量pointNum 要 +1。回溯的时候,就将刚刚加入的分隔符. 删掉就可以了,pointNum也要-1。
for (int i = startIndex; i < s.size(); i++) {if (isValid(s, startIndex, i)) { // 判断 [startIndex,i] 这个区间的子串是否合法s.insert(s.begin() + i + 1 , '.'); // 在i的后面插入一个逗点pointNum++;backtracking(s, i + 2, pointNum); // 插入逗点之后下一个子串的起始位置为i+2pointNum--; // 回溯s.erase(s.begin() + i + 1); // 回溯删掉逗点} else break; // 不合法,直接结束本层循环
}- 判断子串是否合法
主要考虑到如下三点:
- 段位以0为开头的数字不合法
- 段位里有非正整数字符不合法
- 段位如果大于255了不合法
// 判断字符串s在左闭右闭区间[start, end]所组成的数字是否合法
bool isValid(const string& s, int start, int end) {if (start > end) {return false;}if (s[start] == '0' && start != end) { // 0开头的数字不合法return false;}int num = 0;for (int i = start; i <= end; i++) {if (s[i] > '9' || s[i] < '0') { // 遇到非数字字符不合法return false;}num = num * 10 + (s[i] - '0');if (num > 255) { // 如果大于255了不合法return false;}}return true;
}C++代码
class Solution {
private:vector<string> result;// 记录结果// startIndex: 搜索的起始位置,pointNum:添加逗点的数量void backtracking(string& s, int startIndex, int pointNum) {if (pointNum == 3) { // 逗点数量为3时,分隔结束// 判断第四段子字符串是否合法,如果合法就放进result中if (isValid(s, startIndex, s.size() - 1)) {result.push_back(s);}return;}for (int i = startIndex; i < s.size(); i++) {if (isValid(s, startIndex, i)) { // 判断 [startIndex,i] 这个区间的子串是否合法s.insert(s.begin() + i + 1 , '.'); // 在i的后面插入一个逗点pointNum++;backtracking(s, i + 2, pointNum); // 插入逗点之后下一个子串的起始位置为i+2pointNum--; // 回溯s.erase(s.begin() + i + 1); // 回溯删掉逗点} else break; // 不合法,直接结束本层循环}}// 判断字符串s在左闭右闭区间[start, end]所组成的数字是否合法bool isValid(const string& s, int start, int end) {if (start > end) {return false;}if (s[start] == '0' && start != end) { // 0开头的数字不合法return false;}int num = 0;for (int i = start; i <= end; i++) {if (s[i] > '9' || s[i] < '0') { // 遇到非数字字符不合法return false;}num = num * 10 + (s[i] - '0');if (num > 255) { // 如果大于255了不合法return false;}}return true;}
public:vector<string> restoreIpAddresses(string s) {result.clear();if (s.size() < 4 || s.size() > 12) return result; // 算是剪枝了backtracking(s, 0, 0);return result;}
};
LeetCode:78.子集
力扣代码链接
文字讲解:LeetCode:78.子集
视频讲解:回溯算法解决子集问题,树上节点都是目标集和!

基本思路
如果把子集问题、组合问题、分割问题都抽象为一棵树的话,那么组合问题和分割问题都是收集树的叶子节点,而子集问题是找树的所有节点!但是要求解集中不能包含重复的子集,写回溯算法的时候,for就要从startIndex开始,而不是从0开始!(当然如果{1, 2} 和{2, 1}是两个集合,那么我们就需要从0开始)。

- 递归函数参数
全局变量数组path为子集收集元素,二维数组result存放子集组合。
参数:前面已经提到需要传入startIndex,以及整数数组nums。
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums, int startIndex)- 递归终止条件
startIndex表示集合搜索的位置,那么如果startIndex超过了nums的size,不就说明没有元素可取了,也就可以停止循环了,但其实本来startIndex >= nums.size()就是for循环的终止条件。
if (startIndex >= nums.size()) {return;
}- 单层搜索逻辑
求取子集问题,不需要任何剪枝!因为子集就是要遍历整棵树。
for (int i = startIndex; i < nums.size(); i++) {path.push_back(nums[i]); // 子集收集元素backtracking(nums, i + 1); // 注意从i+1开始,元素不重复取path.pop_back(); // 回溯
}C++代码
class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& nums, int startIndex) {result.push_back(path); // 收集子集,要放在终止添加的上面,否则会漏掉自己if (startIndex >= nums.size()) { // 终止条件可以不加return;}for (int i = startIndex; i < nums.size(); i++) {path.push_back(nums[i]);backtracking(nums, i + 1);path.pop_back();}}
public:vector<vector<int>> subsets(vector<int>& nums) {result.clear();path.clear();backtracking(nums, 0);return result;}
};
LeetCode:90.子集II
力扣代码链接
文字讲解:LeetCode:90.子集II
视频讲解:回溯算法解决子集问题,如何去重?

基本思路
这个题目和上一题的区别在于集合里有重复元素了,而且求取的子集要去重。其实和之前做到的组合总和很像,是一个套路。因此理解“树层去重”和“树枝去重”非常重要。

从图中可以看出,同一树层上重复取2就要过滤掉,同一树枝上就可以重复取2,因为同一树枝上元素的集合才是唯一子集!
去重思路和40.组合总和II,这里就直接给出代码。
C++代码
通过used实现去重
class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {result.push_back(path);for (int i = startIndex; i < nums.size(); i++) {// used[i - 1] == true,说明同一树枝candidates[i - 1]使用过// used[i - 1] == false,说明同一树层candidates[i - 1]使用过// 而我们要对同一树层使用过的元素进行跳过if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {continue;}path.push_back(nums[i]);used[i] = true;backtracking(nums, i + 1, used);used[i] = false;path.pop_back();}}public:vector<vector<int>> subsetsWithDup(vector<int>& nums) {result.clear();path.clear();vector<bool> used(nums.size(), false);sort(nums.begin(), nums.end()); // 去重需要排序backtracking(nums, 0, used);return result;}
};通过set实现去重
class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& nums, int startIndex) {result.push_back(path);unordered_set<int> uset;for (int i = startIndex; i < nums.size(); i++) {if (uset.find(nums[i]) != uset.end()) {continue;}uset.insert(nums[i]);path.push_back(nums[i]);backtracking(nums, i + 1);path.pop_back();}}public:vector<vector<int>> subsetsWithDup(vector<int>& nums) {result.clear();path.clear();sort(nums.begin(), nums.end()); // 去重需要排序backtracking(nums, 0);return result;}
};不使用used和set版本
class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& nums, int startIndex) {result.push_back(path);for (int i = startIndex; i < nums.size(); i++) {// 而我们要对同一树层使用过的元素进行跳过if (i > startIndex && nums[i] == nums[i - 1] ) { // 注意这里使用i > startIndexcontinue;}path.push_back(nums[i]);backtracking(nums, i + 1);path.pop_back();}}public:vector<vector<int>> subsetsWithDup(vector<int>& nums) {result.clear();path.clear();sort(nums.begin(), nums.end()); // 去重需要排序backtracking(nums, 0);return result;}
};相关文章:

DAY24|回溯算法Part03|LeetCode:93.复原IP地址、78.子集、90.子集II
目录 LeetCode:93.复原IP地址 基本思路 C代码 LeetCode:78.子集 基本思路 C代码 LeetCode:90.子集II 基本思路 C代码 通过used实现去重 通过set实现去重 不使用used和set版本 LeetCode:93.复原IP地址 力扣代码链接 文字讲解:LeetCode:93.复原IP地…...

接口自动化测试做到什么程度的覆盖算是合格的
接口自动化测试的覆盖程度是一个衡量测试质量与效率的重要指标,其“好”的标准并非绝对,而是根据项目特性和团队需求动态调整的结果。然而,有几个原则和实践可以帮助我们确定一个相对合理的覆盖范围,以及为何这些覆盖是必要的。 1…...

Kubernetes-ArgoCD篇-01-简介
1、什么是Argo CD Argo CD 是针对 Kubernetes 的声明式 GitOps 持续交付工具。 Argo CD官方文档地址:https://argo-cd.readthedocs.io Argo CD源码地址:https://github.com/argoproj/argo-cd 1.1 关于Argo Argo是一个开源的项目,主要是扩…...

阿里云通义大模型团队开源Qwen2.5-Coder:AI编程新纪元
🚀 11月12日,阿里云通义大模型团队宣布开源通义千问代码模型全系列,共6款Qwen2.5-Coder模型。这些模型在同等尺寸下均取得了业界最佳效果,其中32B尺寸的旗舰代码模型在十余项基准评测中均取得开源最佳成绩,成为全球最强…...

【大数据学习 | HBASE高级】hbase的参数优化
Zookeeper 会话超时时间 属性:zookeeper.session.timeout 解释:默认值为 90000 毫秒(90s) hbase.client.pause(默认值 100ms)重试间隔 hbase.client.retries.number(默认 15 次)重试…...

两个链表求并集、交集、差集
两个链表求并集、交集、差集 两个链表求并集、交集、差集其实都是创建一个新链表然后遍历插入的题型,所以下边就举并集一个例子。 首先将l1里的所有节点遍历存储到新节点l中开始遍历l2,如果l中不存在l2中的节点就将其尾插到l中 下面是两个链表求并集、交集、差集的代…...

C++中的栈(Stack)和堆(Heap)
在C中,堆(heap)和栈(stack)是两种用于存储数据的内存区域。理解它们的原理和区别,对于优化代码性能和确保代码的安全性至关重要。以下是对C中堆栈的详细解析,包括它们的分配方式、优缺点、应用场…...

Linux系统编程学习 NO.11——进程的概念(2)
谈谈进程的性质 进程的竞争性 由于CPU资源是稀缺的,进程数量是众多的。不可避免需要造成进程排队等待CPU资源的动作,内核的设计者为了让操作系统合理的去调度这这些进程,就产生了进程优先级的概念。设置合理的进程优先级能让不同进程公平的去竞争CPU资…...

QT自定义控件封装
QT自定义控件封装 1.概述 这篇文章介绍如何创建UI文件,通过自定义方式将两个控件联动起来,实现自定义功能。 2.创建UI文件 新建一个widget的普通项目,然后在项目名称上右键选择And New... 新建文件,然后选择QT 再选择Qt Desig…...

【搜索结构】AVL树的学习与实现
目录 什么是AVL树 AVL树的定义 插入函数的实现 左单旋和右单旋 左右双旋与右左双旋 什么是AVL树 AVL树实际上就是二叉搜索树的一种变体,我们都知道二i叉搜索树可以将查找的时间复杂度提升到O(logn),极大提升搜索效率。但是在极端情况下,当…...

LeetCode40:组合总和II
原题地址:. - 力扣(LeetCode) 题目描述 给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。 candidates 中的每个数字在每个组合中只能使用 一次 。 注意ÿ…...

基于Python+Vue开发的旅游景区管理系统
项目简介 该项目是基于PythonVue开发的旅游景区管理系统(前后端分离),这是一项为大学生课程设计作业而开发的项目。该系统旨在帮助大学生学习并掌握Python编程技能,同时锻炼他们的项目设计与开发能力。通过学习基于Python的旅游景…...

嵌入式硬件杂谈(一)-推挽 开漏 高阻态 上拉电阻
引言:对于嵌入式硬件这个庞大的知识体系而言,太多离散的知识点很容易疏漏,因此对于这些容易忘记甚至不明白的知识点做成一个梳理,供大家参考以及学习,本文主要针对推挽、开漏、高阻态、上拉电阻这些知识点的学习。 目…...

在arm64架构下, Ubuntu 18.04.5 LTS 用命令安装和卸载qt4、qt5
问题:需要在 arm64下安装Qt,QT源码编译失败以后,选择在线安装! 最后安装的版本是Qt5.9.5 和QtCreator 4.5.2 。 一、ubuntu安装qt4的命令(亲测有效): sudo add-apt-repository ppa:rock-core/qt4 sudo apt updat…...

k8s笔记——核心概念
什么是K8s Kubernetes 也称为 K8s,是用于自动部署、扩缩和管理容器化应用程序的开源系统。 Kubernetes 最初是由 Google 工程师作为 Borg 项目开发和设计的,后于 2015 年捐赠给 云原生计算基金会(CNCF)。 什么是 Kubernetes 集群…...

大数据新视界 -- 大数据大厂之 Impala 性能飞跃:动态分区调整的策略与方法(上)(21 / 30)
💖💖💖亲爱的朋友们,热烈欢迎你们来到 青云交的博客!能与你们在此邂逅,我满心欢喜,深感无比荣幸。在这个瞬息万变的时代,我们每个人都在苦苦追寻一处能让心灵安然栖息的港湾。而 我的…...
)
开源模型应用落地-qwen模型小试-Qwen2.5-7B-Instruct-tool usage入门-并行调用多个tools(五)
一、前言 Qwen-Agent 是一个利用开源语言模型Qwen的工具使用、规划和记忆功能的框架。其模块化设计允许开发人员创建具有特定功能的定制代理,为各种应用程序提供了坚实的基础。同时,开发者可以利用 Qwen-Agent 的原子组件构建智能代理,以理解和响应用户查询。 本篇将介绍如何…...

蓝桥杯每日真题 - 第8天
题目:(子2023) 题目描述(14届 C&C B组A题) 解题思路: 该代码通过动态计算包含数字 "2023" 的子序列出现次数。主要思路是: 拼接序列:将1到2023的所有数字按顺序拆分…...

论云游戏的性能与性价比,ToDesk、青椒云、顺网云游戏等具体实操看这篇就够了
文章目录 一、前言二、云电脑产品基础介绍2.1 ToDesk云电脑2.1.1 ToDesk云电脑硬件参数2.1.2 ToDesk云电脑鲁大师跑分2.1.3 ToDesk云电脑收费方式2.1.4 ToDesk云电脑特色功能 2.2 青椒云2.2.1 青椒云游戏娱乐硬件配置2.2.2 青椒云云电脑鲁大师跑分2.2.3 青椒云收费方式2.2.4 青…...
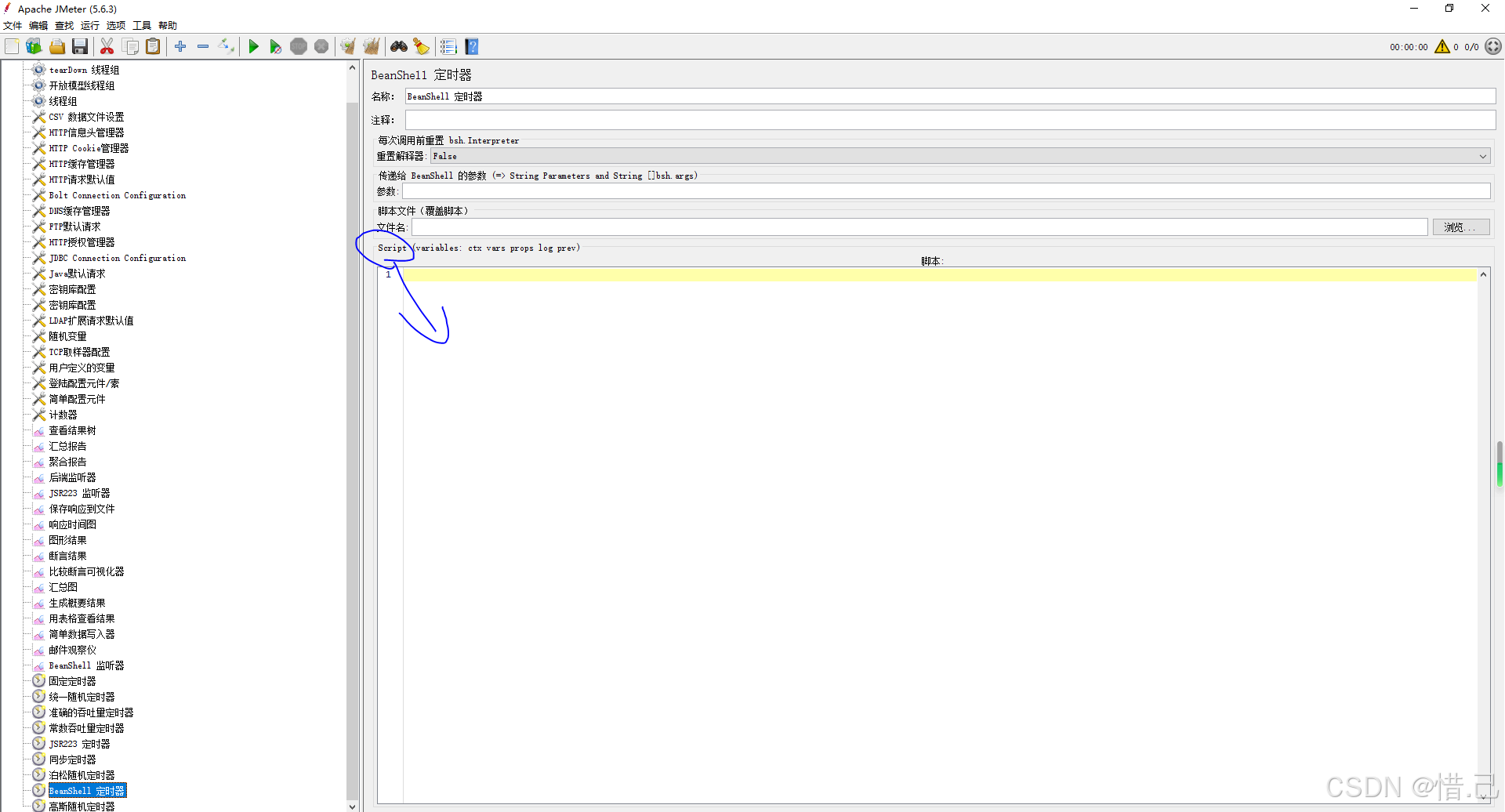
Jmeter中的定时器(二)
5--JSR223 Timmer 功能特点 自定义延迟逻辑:使用脚本语言动态计算请求之间的延迟时间。灵活控制:可以根据测试数据和条件动态调整延迟时间。支持多种脚本语言:支持 Groovy、JavaScript、BeanShell 等多种脚本语言。 支持的脚本语言 Groov…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...
