【搜索结构】AVL树的学习与实现
目录
什么是AVL树
AVL树的定义
插入函数的实现
左单旋和右单旋
左右双旋与右左双旋
什么是AVL树
AVL树实际上就是二叉搜索树的一种变体,我们都知道二i叉搜索树可以将查找的时间复杂度提升到O(logn),极大提升搜索效率。但是在极端情况下,当按顺序向树插入节点时,二叉树严重不平衡,相当于退化成了链表,此时查找的时间复杂度就变为了O(n),这并不是我们希望看到的。
那么有没有什么方式可以让二叉搜索树保持一定的平衡性从而不至于导致查找效率严重降低呢?AVL树也就是高度平衡二叉树给出的解决方案是:
1. 二叉树的每个节点都有一个平衡因子,平衡因子等于左子树高度减右子树高度的值
2. 平衡因子的绝对值不能超过1
3. 当插入或删除节点导致平衡因子绝对值超过1时,进行旋转
AVL树的定义
让我们来思考一下,要实现前面描述的功能,AVL树的单个节点应该有哪些成员变量呢?
1. 首先肯定要有左右子树的节点
2. 然后为了旋转时能够找到父亲,我们还需要存父亲节点
3. 为了确保平衡,我们要将左右高度差作为平衡因子保存
4. 最后还有搜索要用到的键值对
AVL树节点类定义:
template<class K, class V>
struct AVLTreeNode
{// 由于插入节点时要向上更新,所以使用三叉链结构AVLTreeNode<K, V>* left;AVLTreeNode<K, V>* right;AVLTreeNode<K, V>* parent; pair<K, V> _kv; // 键值int _bf; // 平衡因子AVLTreeNode(const pair<K, V>& kv):_kv(kv), left(nullptr),right(nullptr),parent(nullptr),_bf(0){}
};那么,AVL树的定义就应该是:
template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
private:Node* _root = nullptr;
};插入函数的实现
让我们先明确一下AVL树插入一个节点要做的事:
1. 按照二叉搜索树的规则找到插入位置进行插入
2. 根据左右高度差得到平衡因子
3. 当平衡因子绝对值大于1时进行旋转处理
首先二叉树搜索规则就是:当插入节点的键小于当前节点的键时,和当前节点的左子树进行比较;当插入节点的键大于当前节点的键时,和当前节点的右子树进行比较;否则说明插入节点的键已经存在,这不符合二叉搜索树的规则,直接报错。我们按照这个规则找到可以插入的位置然后将新节点插入。
插入完成之后,我们开始更新平衡因子,当新节点位于父亲的左边时,bf减1;当位于父亲的右边时,bf加1。修改完父亲的平衡因子后,进行判断:
1. 如果当前父亲平衡因子值为0,说明高度差没有改变,不需要进行处理,直接break即可。
2. 如果当前父亲平衡因子值为1/-1,说明插入导致高度差改变了,这可能会导致祖先节点的平衡因子绝对值超过1,所以需要继续往上更新祖先的平衡因子
3. 如果更新后的祖先的平衡因子绝对值超过1,就需要进行旋转处理
为了更直观地理解这个过程,让我们来看一个简单的例子:
插入新节点导致祖先失去平衡:

通过旋转,使AVL树恢复平衡

我们可以看到,这棵树的根节点平衡因子在插入新节点后,由1变为2,而进行一次左旋之后,平衡因子更新为0,恢复了平衡。
由于旋转涉及到的情况比较多且有一些细节操作,而这只是其中最简单的一种情况,所以我们先写出AVL树插入的基本框架,之后再对各个需要旋转的情况分别进行处理。
bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr; // 用于记录插入位置的父亲节点Node* cur = _root; // 用于比较查找到插入位置while (cur){parent = cur;if (kv.first < cur->_kv.first){cur = cur->left;}else if (kv.first > cur->_kv.first){cur = cur->right;}// 搜索二叉树不支持重复key值的情况else{return false;}}// 此时说明已经找到了插入位置,插入新节点cur = new Node(kv);if (kv.first < parent->_kv.first){parent->left = cur;}else{parent->right = cur;}cur->parent = parent; // 记得保持三叉链结构// 更新平衡因子while (parent){if (cur == parent->left){parent->_bf--;}else{parent->_bf++;}// 正好平衡了if (parent->_bf == 0){break;}// 说明需要向上调整else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->parent;}// 在此处进行旋转调整else if (parent->_bf == 2 || parent->_bf == -2){// 旋转处理……}// 说明旋转有问题,不能在|bf|==2时恢复平衡else{assert(false);}}return true;}左单旋和右单旋
先来看左单旋,如下图所示,是左单旋最简单的情况:

但显然需要左单旋的情况通常会更复杂些,所以我们实现左单旋时,需要考虑具有通用性的情况:

可以发现,我们的左单旋操作似乎只需要让parent的右指向subRL,然后让subR的左指向parent。但大家可别忘了,我们定义AVL树节点时,为了方便向上更新,设计的是三叉链结构,所以还需要更新subRL和parent的父亲节点。除此之外,还需要考虑到parent可能是祖先节点的孩子,所以如果parent是AVL树的根节点:将根节点更新为subR,并将subR的父亲更新为nullptr;如果parent是祖先节点的孩子:则将祖先节点的孩子更新为subR,并将subR的父亲更新为父亲节点。
指针朝向修改完后,我们还需要修改发生高度变化的节点的平衡因子,如上图所示,parent的平衡因子由2变为0,subR的平衡因子由1变为0。
void RotateL(Node* parent)
{// 在修改之前先保存祖父节点Node* grandpa = parent->parent;// 事实上,对于左旋这一情况,我们要修改的只有parent,subR,subRL最多再加个grandpa的指针朝向Node* subR = parent->right;Node* subRL = subR->left;// 进行左旋操作parent->right = subRL;subR->left = parent;// 之后还得把父指针也一起修改了parent->parent = subR;if(subRL)subRL->parent = parent;// 这棵树不是子树if (parent == _root){_root = subR;_root->parent = nullptr;}// 这棵树是子树else{// 是祖父节点的左子树if (grandpa->left == parent){grandpa->left = subR;}// 是祖父节点的右子树else{grandpa->right = subR;}subR->parent = grandpa;}parent->_bf = subR->_bf = 0;}接下来是右单旋,在局部子树左偏时,我们通过右旋来进行处理:

由于在左单旋部分我们已经详细讲解过了,右单旋其实就相当于反过来,所以就不再讲解一遍了。
void RotateR(Node* parent){// 在修改之前先保存祖父节点Node* grandpa = parent->parent;// 事实上,对于右旋这一情况,我们要修改的只有parent,subL,subLR最多再加个grandpa的指针朝向Node* subL = parent->left;Node* subLR = subL->right;// 进行右旋操作parent->left = subLR;subL->right = parent;// 之后还得把父指针也一起修改了parent->parent = subL;if (subLR)subLR->parent = parent;// 需要考虑现在调整的这棵树是子树的情况if (parent == _root){_root = subL;_root->parent = nullptr;}else{// 是祖父节点的左子树if (grandpa->left == parent){grandpa->left = subL;}// 是祖父节点的右子树else{grandpa->right = subL;}subL->parent = grandpa;}parent->_bf = subL->_bf = 0;
}左右双旋与右左双旋
我们还是先来看一个左右双旋的简单例子,可以看到,我们先通过一次左旋,把这棵子树修改为了单纯的左偏,而处理左偏,我们只需要进行一次右旋即可。

再来看更普遍的情况:

事实上,由于我们已经有了左旋和右旋的代码,所以进行双旋时,可以直接复用左旋和右旋函数,所以双旋主要考虑的是如何更新平衡因子。
一共有三种情况:
第一种:60就是新增节点,此时平衡因子全部更新为0
第二种:新增节点向b插入,此时parent的因子为1,其余因子为0
第三种:新增节点向c插入,此时subL的因子为-1,其余因子为0
大家可以自己分别画一下这三种情况,其实自己动手画一下就很好理解了,让我们看代码:
void RotateLR(Node* parent){Node* subL = parent->left;Node* subLR = subL->right;// 啊啊啊,原来是这里错了,调试了一个晚上。。// int bf = parent->_bf;int bf = subLR->_bf;RotateL(parent->left);RotateR(parent);if (bf == 0){parent->_bf = subL->_bf = subLR->_bf = 0;}else if (bf == -1){parent->_bf = 1;subLR->_bf = 0;subL->_bf = 0;}else if (bf == 1){parent->_bf = 0;subLR->_bf = 0;subL->_bf = -1;}//else//{// assert(false);//}}
右左双旋和左右双旋完全类似,也是三种情况,其实理解了左右双旋,右左双旋就很好写了!
void RotateRL(Node* parent){Node* subR = parent->right;Node* subRL = subR->left;// 提前记录修改点的平衡因子int bf = subRL->_bf;// 先右旋RotateR(parent->right);// 再左旋RotateL(parent);if (bf == 0){// 自己就是新增节点parent->_bf = subR->_bf = subRL->_bf = 0;}else if (bf == -1){// 新增节点位于subRL的左子树parent->_bf = 0;subRL->_bf = 0;subR->_bf = 1;}else if (bf == 1){// 新增节点位于subRL的右子树parent->_bf = -1;subRL->_bf = 0;subR->_bf = 0;}//else//{// assert(false);//}}相关文章:

【搜索结构】AVL树的学习与实现
目录 什么是AVL树 AVL树的定义 插入函数的实现 左单旋和右单旋 左右双旋与右左双旋 什么是AVL树 AVL树实际上就是二叉搜索树的一种变体,我们都知道二i叉搜索树可以将查找的时间复杂度提升到O(logn),极大提升搜索效率。但是在极端情况下,当…...

LeetCode40:组合总和II
原题地址:. - 力扣(LeetCode) 题目描述 给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。 candidates 中的每个数字在每个组合中只能使用 一次 。 注意ÿ…...

基于Python+Vue开发的旅游景区管理系统
项目简介 该项目是基于PythonVue开发的旅游景区管理系统(前后端分离),这是一项为大学生课程设计作业而开发的项目。该系统旨在帮助大学生学习并掌握Python编程技能,同时锻炼他们的项目设计与开发能力。通过学习基于Python的旅游景…...

嵌入式硬件杂谈(一)-推挽 开漏 高阻态 上拉电阻
引言:对于嵌入式硬件这个庞大的知识体系而言,太多离散的知识点很容易疏漏,因此对于这些容易忘记甚至不明白的知识点做成一个梳理,供大家参考以及学习,本文主要针对推挽、开漏、高阻态、上拉电阻这些知识点的学习。 目…...

在arm64架构下, Ubuntu 18.04.5 LTS 用命令安装和卸载qt4、qt5
问题:需要在 arm64下安装Qt,QT源码编译失败以后,选择在线安装! 最后安装的版本是Qt5.9.5 和QtCreator 4.5.2 。 一、ubuntu安装qt4的命令(亲测有效): sudo add-apt-repository ppa:rock-core/qt4 sudo apt updat…...

k8s笔记——核心概念
什么是K8s Kubernetes 也称为 K8s,是用于自动部署、扩缩和管理容器化应用程序的开源系统。 Kubernetes 最初是由 Google 工程师作为 Borg 项目开发和设计的,后于 2015 年捐赠给 云原生计算基金会(CNCF)。 什么是 Kubernetes 集群…...

大数据新视界 -- 大数据大厂之 Impala 性能飞跃:动态分区调整的策略与方法(上)(21 / 30)
💖💖💖亲爱的朋友们,热烈欢迎你们来到 青云交的博客!能与你们在此邂逅,我满心欢喜,深感无比荣幸。在这个瞬息万变的时代,我们每个人都在苦苦追寻一处能让心灵安然栖息的港湾。而 我的…...
)
开源模型应用落地-qwen模型小试-Qwen2.5-7B-Instruct-tool usage入门-并行调用多个tools(五)
一、前言 Qwen-Agent 是一个利用开源语言模型Qwen的工具使用、规划和记忆功能的框架。其模块化设计允许开发人员创建具有特定功能的定制代理,为各种应用程序提供了坚实的基础。同时,开发者可以利用 Qwen-Agent 的原子组件构建智能代理,以理解和响应用户查询。 本篇将介绍如何…...

蓝桥杯每日真题 - 第8天
题目:(子2023) 题目描述(14届 C&C B组A题) 解题思路: 该代码通过动态计算包含数字 "2023" 的子序列出现次数。主要思路是: 拼接序列:将1到2023的所有数字按顺序拆分…...

论云游戏的性能与性价比,ToDesk、青椒云、顺网云游戏等具体实操看这篇就够了
文章目录 一、前言二、云电脑产品基础介绍2.1 ToDesk云电脑2.1.1 ToDesk云电脑硬件参数2.1.2 ToDesk云电脑鲁大师跑分2.1.3 ToDesk云电脑收费方式2.1.4 ToDesk云电脑特色功能 2.2 青椒云2.2.1 青椒云游戏娱乐硬件配置2.2.2 青椒云云电脑鲁大师跑分2.2.3 青椒云收费方式2.2.4 青…...
Jmeter中的定时器(二)
5--JSR223 Timmer 功能特点 自定义延迟逻辑:使用脚本语言动态计算请求之间的延迟时间。灵活控制:可以根据测试数据和条件动态调整延迟时间。支持多种脚本语言:支持 Groovy、JavaScript、BeanShell 等多种脚本语言。 支持的脚本语言 Groov…...

华为HCIP-openEuler考试内容大纲:备考必看!
华为HCIP-openEuler认证考试作为ICT领域的一项重要技术认证,已经成为越来越多IT从业者追求的目标。无论你是想提升自己的技术能力,还是为了未来的职业发展,HCIP-openEuler都是一个极具价值的认证。那么,如何高效备考,顺…...

Vector 深度复制记录
有的时候数据得复制过去 有个疑问,自动分配内存吗? 不是估计有变化, 得在看看 指针作为值复制了 … … 挺好,修改原有的值 x86 的 SIM 程序 还有点问题 ; 无法直接绕过硬件错误 。。。 x86 gdb 没有问题 就是运行出现了问题,怎么解决;正常初始化没有问题…...
Go语言实现用户登录Web应用
文章目录 1. Go语言Web框架1.1 框架比较1.2 安装Gin框架 2. 实现用户登录功能2.1 创建项目目录2.2 打开项目目录2.3 创建登录Go程序2.4 创建模板页面2.4.1 登录页面2.4.2 登录成功页面2.4.3 登录失败页面 3. 测试用户登录项目3.1 运行登录主程序3.2 访问登录页面3.3 演示登录成…...

Android CarrierConfig 参数项和正则匹配逻辑
背景 在编写CarrierConfig的时候经常出现配置不生效的情况,比如运营商支持大范围的imsi,或者是测试人员写卡位数的问题等等,因此就需要模式匹配(包含但不限于正则表达式)。 基本概念: 模式匹配涉及定义一个“模式”&a…...

微信小程序中使用离线版阿里云矢量图标
前言 阿里矢量图库提供的在线链接服务仅供平台体验和调试使用,平台不承诺服务的稳定性,企业客户需下载字体包自行发布使用并做好备份。 1.下载图标 将阿里矢量图库的图标先下载下来 解压如下 2.转换格式 贴一个地址用于转换格式:Onlin…...

hive的tblproperties支持修改的属性
文章目录 一、介绍二、查看TBLPROPERTIES属性三、修改TBLPROPERTIES属性 一、介绍 TBLPROPERTIES用途:向表中添加自定义或预定义的元数据属性,并设置它们的赋值。在hive建表时,可设置TBLPROPERTIES参数修改表的元数据,也能通过AL…...

移动端开发
一、一些概念 (一)、屏幕相关 1、屏幕大小 指屏幕的对角线长度,单位是英寸(inch)。常用尺寸有:3.5寸、4.7寸、5.0寸、5.5寸、6.0寸等 备注:1英寸(inch)2.54厘米&…...

光伏行业内卷到什么程度了?
现在每个行业都在内卷,光伏行业也一样在内卷中,但是光伏行业的内卷体现在多个方面,下面给举例。 一、产能竞争激烈: 产能扩张迅速:过去几年,大量资本涌入光伏行业,企业纷纷扩产。例如…...

C# 通俗易懂的介绍基础知识(七)——栈Stack(从日常生活开始讲解)
目录 一、前言 二、栈是排列方式 三、栈的单词 四、程序中的栈 五、栈的方法 1.声明并初始化栈 2.往栈里放东西(学名:入栈) 3.从栈往外拿东西 (学名:出栈) 4.清空栈 5.遍历 Stack 6.获取Stack的长…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...
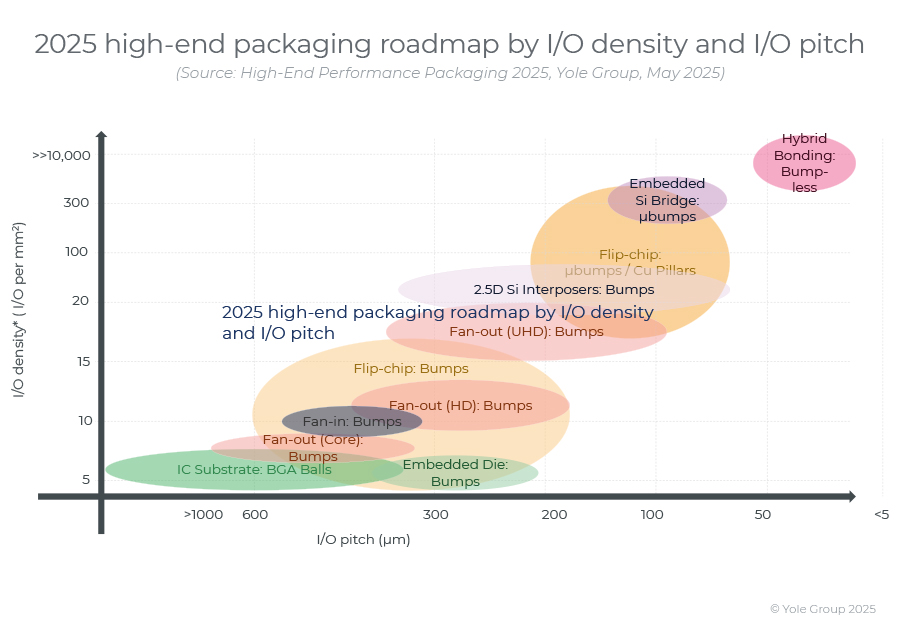
高端性能封装正在突破性能壁垒,其芯片集成技术助力人工智能革命。
2024 年,高端封装市场规模为 80 亿美元,预计到 2030 年将超过 280 亿美元,2024-2030 年复合年增长率为 23%。 细分到各个终端市场,最大的高端性能封装市场是“电信和基础设施”,2024 年该市场创造了超过 67% 的收入。…...

解决MybatisPlus使用Druid1.2.11连接池查询PG数据库报Merge sql error的一种办法
目录 前言 一、问题重现 1、环境说明 2、重现步骤 3、错误信息 二、关于LATERAL 1、Lateral作用场景 2、在四至场景中使用 三、问题解决之道 1、源码追踪 2、关闭sql合并 3、改写处理SQL 四、总结 前言 在博客:【写在创作纪念日】基于SpringBoot和PostG…...
Web APIS Day01
1.声明变量const优先 那为什么一开始前面就不能用const呢,接下来看几个例子: 下面这张为什么可以用const呢?因为复杂数据的引用地址没变,数组还是数组,只是添加了个元素,本质没变,所以可以用con…...

在MobaXterm 打开图形工具firefox
目录 1.安装 X 服务器软件 2.服务器端配置 3.客户端配置 4.安装并打开 Firefox 1.安装 X 服务器软件 Centos系统 # CentOS/RHEL 7 及之前(YUM) sudo yum install xorg-x11-server-Xorg xorg-x11-xinit xorg-x11-utils mesa-libEGL mesa-libGL mesa-…...
