数据结构 -二叉搜索树
一.什么是二叉搜索树

树插入删除方便比线性数组


二.二叉搜索树的查找操作


尾递归可以用循环递归



三.二叉树的插入操作

35要挂在33上面必须记住33的位置
解决方法,要求递归函数返回一个 结点插到33的右子树


四.二叉搜索树的删除

要是删除的是叶子节点之间删除

只有一个结点,删除33这个节点,删除之后33的父节点指向子孙结点35

好处左子树的最大值,右子树的最小值一定不是有两个孩子的结点,左子树的最大值一定在最右边,右子树的最小值一定在最左边边
变成了前面的情况要么没儿子要么只要一个

假设要删除的值在左子树
BST->Left=Delete(X,BST->Left),从这个树里删除这个结点变成从左子树里删除这个结点
左子树删除完之后有可能根节点发生变化
有一种情况删除的是下面的结点跟不变,另一种左子树只有一个结点这个结点就是你要删除的结点,所以左子树便空了返回NULL
BTS=BTS->Left,删除一个结点之后返回新的左子树根节点的地址
Tmp=FindMin(BTS->Right)从右子树里找最小值
然后BTS->Data=Tmp->Data替代这个要被删除的结点
然后BST->Right=Delete(BTS->Data,BTS->Right)再删除这个右子树里的最小值
找到要删除的结点且左右子树有一个不为空,
if(!BTS-<Left)这个结点的左子树为空就
BST=BST->Right把这个结点右子树赋给要删除的结点
return BST将来再返回这个结点
左右两边都空的情况,左边空了右边进行复制右边是空
#include<iostream>
using namespace std;
#include<queue>
typedef int ElementType;
typedef struct TNode* poist;
typedef poist BinTree;
typedef struct TNode {ElementType Data;BinTree L;BinTree R;
};BinTree Insert(BinTree BTS,ElementType x) {if (!BTS) {BTS = new TNode();BTS->Data = x;BTS->L = BTS->R = NULL;}else {if (x < BTS->Data) {BTS->L = Insert(BTS->L, x);}else if (x > BTS->Data) {BTS->R = Insert(BTS->R, x);}}return BTS;
}BinTree Find(BinTree BTS, ElementType x) {if (!BTS) return NULL;if (x < BTS->Data)return Find(BTS->L, x);else if (x > BTS->Data)return Find(BTS->R, x);elsereturn BTS;}
BinTree Find(ElementType x, BinTree BTS) {while (BTS) {if (x < BTS->Data)BTS = BTS->L;else if (x > BTS->Data)BTS = BTS->R;elsereturn BTS;}return NULL;
}
void banli(BinTree BTS) {if (BTS) {cout << BTS->Data << " ";banli(BTS->L);banli(BTS->R);}
}
BinTree FindMax(BinTree BTS) {if (BTS) {while (BTS->R)BTS = BTS->R;}return BTS;
}
BinTree FindMin(BinTree BTS) {if (!BTS)return NULL;else if (!BTS->L)return BTS;elsereturn FindMin(BTS->L);
}
BinTree Delete(ElementType x, BinTree BTS) {poist Tmp;if (!BTS)cout << "要删除的元素未找到";else if (x < BTS->Data)BTS->L = Delete(x, BTS->L);else if (x > BTS->Data)BTS->R = Delete(x, BTS->R);elseif (BTS->L && BTS->R) {Tmp = FindMin(BTS->R);BTS->Data = Tmp->Data;BTS->R = Delete(BTS->Data, BTS->R);}else {Tmp = BTS;if (!BTS->L)BTS = BTS->R;else if (!BTS->R)BTS = BTS->L;delete Tmp;}return BTS;
}
int main()
{BinTree T2;BinTree T1 = new TNode();T1->Data = 22;Insert(T1, 3);Insert(T1, 7);Insert(T1, 8);Insert(T1, 1);Insert(T1, 19);Insert(T1, 12);Insert(T1, 6);T2 = Find(T1,1);cout <<"查找:" << T2->Data << endl;T2 = Find(12, T1);cout << "查找:"<<T2->Data << endl;T2 = FindMax(T1);cout <<"查找最大值:"<< T2->Data << endl;T2 = FindMin(T1);cout << "查找最小值:" << T2->Data << endl;cout << "删除前:";banli(T1);cout << endl;cout << "删除后";T1= Delete(22, T1);banli(T1);return 0;
}相关文章:

数据结构 -二叉搜索树
一.什么是二叉搜索树 树插入删除方便比线性数组 二.二叉搜索树的查找操作 尾递归可以用循环递归 三.二叉树的插入操作 35要挂在33上面必须记住33的位置 解决方法,要求递归函数返回一个 结点插到33的右子树 四.二叉搜索树的删除 要是删除的是叶子节点之间删除 只有一…...

Ubuntu配置阿里云docker apt源
一、配置阿里云docker apt源 Ubuntu 放弃了apt-key的GPG 密钥的管理方法,用户可以直接添加gpg密钥到/etc/apt/trusted.gpg.d/目录下。 同时添加删除apt source 直接在/etc/apt/sources.list.d/目录下操作即可。 1、删除旧的镜像源 #旧版操作方法 apt-key list # …...

【React】状态管理之Redux
🌈个人主页: 鑫宝Code 🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础 💫个人格言: "如无必要,勿增实体" 文章目录 状态管理之Redux引言1. Redux 的核心概念1.1 单一数据源(Single Sou…...

3195. 有趣的数-13年12月CCF计算机软件能力认证(组合数)
题目 思路 统计方案的时候先去分类,先放01,然后在考虑23对于第k类, 对于01的选择 对于所有的分类:本题我觉得要考虑的几个点就是:状态分类得到数学公式组合数的计算防越界处理 代码 计算组合数的代码模板࿱…...

基于 Python 的 Bilibili 评论分析与可视化
一、项目概述 本项目利用 Python 对 Bilibili (哔哩哔哩)平台上的视频评论数据进行爬取、清洗和分析,并通过可视化展示数据的主要特征。我们通过以下几个步骤实现了这一过程: 数据爬取:使用 Bilibili 提供的 API 获取…...

大语言模型理论基础
文章目录 前言大语言模型必需知识概述大语言模型目标模型上下文神经网络的神经元常见激活函数SigmoidTanhRelusoftmax 通用近似定理多层感知机(MLP)拟合最后 前言 你好,我是醉墨居士,我们接下来对大语言模型一探究竟,…...
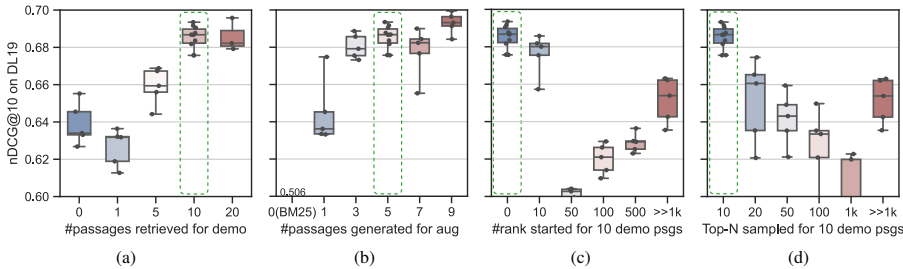
【 LLM论文日更|检索增强:大型语言模型是强大的零样本检索器 】
论文:https://aclanthology.org/2024.findings-acl.943.pdf代码:GitHub - taoshen58/LameR机构:悉尼科技大学 & 微软 & 阿姆斯特丹大学 & 马里兰大学领域:retrieval & llm发表:ACL2024 研究背景 研究…...

【基于轻量型架构的WEB开发】课程 作业3 Spring框架
一. 单选题(共12题,48分) 1. (单选题)以下有关Spring框架优点的说法不正确的是( )。 A. Spring就大大降低了组件之间的耦合性。 B. Spring是一种侵入式框架 C. 在Spring中,可以直接通过Spring配置文件管理…...

14.最长公共前缀-力扣(LeetCode)
题目: 解题思路: 解决本题的关键点是确定扫描的方式,大体上有两种方式:横向扫描和纵向扫描。 1、横向扫描:首先比较第一个字符串和第二个字符串,记录二者的公共前缀,然后用当前公共前缀与下一个…...

客户案例|智能进化:通过大模型重塑企业智能客服体验
01 概 述 随着人工智能技术的快速发展,客户对服务体验的期待和需求不断升级。在此背景下,大模型技术的崛起,为智能客服领域带来了创造性的变革。 在上篇文章《在后LLM时代,关于新一代智能体的思考》中有提到,智能客服…...

Flink Job更新和恢复
Checkpoints 的主要目的是为意外失败的作业提供恢复机制。 Savepoints的设计更侧重于可移植性和操作灵活性,尤其是在 job 变更方面。Savepoint 的用例是针对计划中的、手动的运维。例如,可能是更新你的 Flink 版本,更改你的作业图等等。 fli…...

读多写少业务中,MySQL如何优化数据查询方案?
小熊学Java站点:https://www.javaxiaobear.cn 编程资料合集:https://pqgmzk7qbdv.feishu.cn/base/QXq2bY5OQaZiDksJfZMc30w5nNb?from=from_copylink 看一看当面试官提及“在读多写少的网络环境下,MySQL 如何优化数据查询方案”时,你要从哪些角度出发回答问题??? 案例…...

Bugku CTF_Web——点login咋没反应
Bugku CTF_Web——点login咋没反应 进入靶场 随便输个试试 看来确实点login没反应 抓包看看 也没有什么信息 看了下源码 给了点提示 一个admin.css try ?12713传参试试 拿到一个php代码 <?php error_reporting(0); $KEYctf.bugku.com; include_once("flag.php&q…...

attention 注意力机制 学习笔记-GPT2
注意力机制 这可能是比较核心的地方了。 gpt2 是一个decoder-only模型,也就是仅仅使用decoder层而没有encoder层。 decoder层中使用了masked-attention 来进行注意力计算。在看代码之前,先了解attention-forward的相关背景知识。 在普通的self-atten…...

什么是HTTP,什么是HTTPS?HTTP和HTTPS都有哪些区别?
什么是 HTTP? HTTP(Hypertext Transfer Protocol,超文本传输协议)是一种应用层协议,用于在互联网上进行数据通信。它定义了客户端(通常是浏览器)和服务器之间的请求和响应格式。HTTP 是无状态的…...

SkyWalking-安装
SkyWalking-简单介绍 是一个开源的分布式追踪系统,用于检测、诊断和优化分布式系统的功能。 支持 ElasticSearch、H2、MySQL、PostgreSql 等数据库 基于 ElasticSearch 的情况 ElasticSearch(ES) 安装 1、下载并解压 https://www.elastic…...

RabbitMQ运维
1. 单机多节点 1.1 搭建RabbitMQ ①安装RabbitMQ 略 ②确认RabbitMQ运⾏没问题 #查看RabbitMQ状态 rabbitmqctl status 节点名称: 端口号: 25672:Erlang分布式节点通信的默认端⼝, Erlang是RabbitMQ的底层通信协议.15672: Web管理界⾯的默认端⼝, 通过这个端⼝可以访问R…...

Go语言并发精髓:深入理解和运用go语句
Go语言并发精髓:深入理解和运用go语句 在Go语言的世界里,go语句是实现并发的核心,它简洁而强大,允许程序以前所未有的方式运行多个任务。本文将深入探讨go语句及其执行规则,揭示Go语言并发编程的内在机制,并提供实际案例帮助读者掌握其用法。 1. go语句的基本概念(Wha…...

基于STM32的智能家居系统:MQTT、AT指令、TCP\HTTP、IIC技术
一、项目概述 随着智能家居技术的不断发展,越来越多的家庭开始使用智能设备来提升生活质量和居住安全性。智能家居系统不仅提供了便利的生活方式,还能有效地监测家庭环境,保障家庭安全。本项目以设计一种基于STM32单片机的智能家居系统为目标…...

分糖果(相等分配)
题目:有n种不同口味的糖果,第i种糖果的数量为a[i],现在需要把糖果分给m个人。分给每个人糖果的数量必须是相等的,并且每个人只能选择一种糖果。也就是说,可以把一种糖果分给多个人,但是一个人的糖果不能有多…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...
