Day44 | 动态规划 :状态机DP 买卖股票的最佳时机IV买卖股票的最佳时机III
Day44 | 动态规划 :状态机DP 买卖股票的最佳时机IV&&买卖股票的最佳时机III&&309.买卖股票的最佳时机含冷冻期
动态规划应该如何学习?-CSDN博客
本次题解参考自灵神的做法,大家也多多支持灵神的题解
买卖股票的最佳时机【基础算法精讲 21】_哔哩哔哩_bilibili
希望读者在阅读之前先看完这篇博客
Day43 | 动态规划 :状态机DP 买卖股票的最佳时机&&买卖股票的最佳时机II-CSDN博客
动态规划学习:
1.思考回溯法(深度优先遍历)怎么写
注意要画树形结构图
2.转成记忆化搜索
看哪些地方是重复计算的,怎么用记忆化搜索给顶替掉这些重复计算
3.把记忆化搜索翻译成动态规划
基本就是1:1转换
文章目录
- Day44 | 动态规划 :状态机DP 买卖股票的最佳时机IV&&买卖股票的最佳时机III&&309.买卖股票的最佳时机含冷冻期
- 188.买卖股票的最佳时机IV
- 思路分析(子问题):
- 1.回溯 DFS
- 2.记忆化搜索
- 3.1:1翻译为动态规划
- 4.滚动数组优化
- 123.买卖股票的最佳时机III
188.买卖股票的最佳时机IV
188. 买卖股票的最佳时机 IV - 力扣(LeetCode)
思路分析(子问题):
状态机的变化:多了一个参数j表示我们最多可以交易几笔
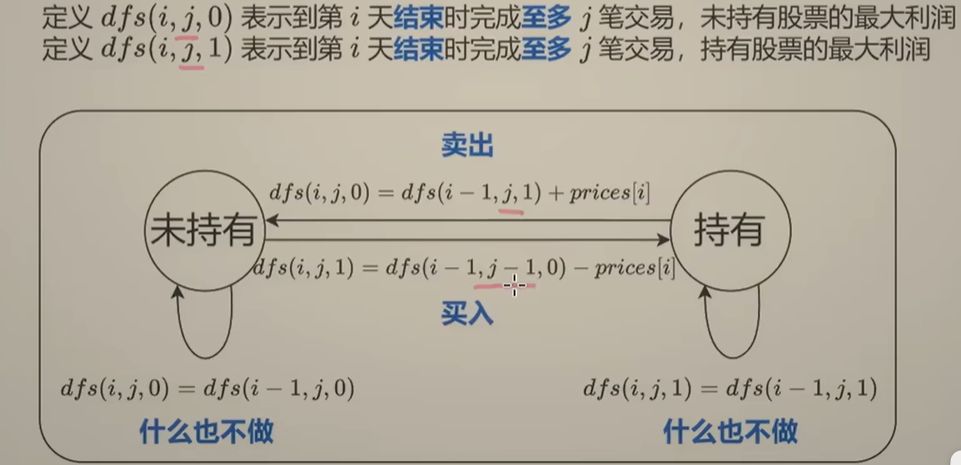
在加减prices[i]的时候进行j-1,表示我们进行了一笔交易,那剩下在递归的时候最多只能交易j-1次
注意:j-1只在加prices[i]或者减prices[i]的时候写一次,加表示我们卖出,可以看做一次交易,减表示一次买进,也可以看做一次交易,但是加减prices[i]的时候都写,就说明我们买进一次再卖出算成了两次交易,这样就错了

笔者觉得在卖出的时候进行交易次数的计算比较好,就使用这个
递归边界部分,和前两道题不同的就是j如果小于0了那肯定就是不合法的状态,因为我们的交易次数最少应该是0,所以就返回一个负无穷表示这是不合法的
1.回溯 DFS
1.返回值和参数
i是每天的价格
status是状态,表示是否持有股票
j是我们现在最多可以交易多少笔
dfs返回值是我们在前i天持有或者不持有股票,在最多交易j次的前提下可以获得的最大利润
int dfs(int i,int j,int status,vector<int>& prices)
2.终止条件
就是在前两题的基础上了一个不合法的状态,那就是交易次数小于0的话要返回负无穷
注意判断的顺序,交易次数j一定要先判断,因为只要j小于0那肯定是不合法的
if(j<0)return INT_MIN;if(i<0)if(status==1) return INT_MIN;elsereturn 0;
3.本层逻辑
在我们加prices[i]的时候,就说明是卖出股票,就说明第i天进行了一次交易,第i天的利润是prices[i],那前i-1天的利润就是在最多交易j-1笔的情况下的最大利润,传入j-1
if(status==1)return max(dfs(i-1,j,1,prices),dfs(i-1,j,0,prices)-prices[i]);elsereturn max(dfs(i-1,j,0,prices),dfs(i-1,j-1,1,prices)+prices[i]);
完整代码:
当然,这是超时的
class Solution {
public:int dfs(int i,int j,int status,vector<int>& prices){if(j<0)return INT_MIN;if(i<0)if(status==1) return INT_MIN;elsereturn 0;if(status==1)return max(dfs(i-1,j,1,prices),dfs(i-1,j,0,prices)-prices[i]);elsereturn max(dfs(i-1,j,0,prices),dfs(i-1,j-1,1,prices)+prices[i]);}int maxProfit(int k,vector<int>& prices) {return dfs(prices.size()-1,k,0,prices);}
};
2.记忆化搜索
就是搞一个哈希表dp,全都初始化为-1,每次返回前给哈希表dp赋值,碰到不是-1的那就是算过的,那就直接返回计算过的结果,不需要再次递归了
class Solution {
public:int dfs(int i,int j,int status,vector<int>& prices,vector<vector<vector<int>>>& dp){if(j<0)return INT_MIN;if(i<0)if(status==1) return INT_MIN;elsereturn 0;if(dp[i][j][status]!=-1)return dp[i][j][status];if(status==1)return dp[i][j][status]=max(dfs(i-1,j,1,prices,dp),dfs(i-1,j,0,prices,dp)-prices[i]);elsereturn dp[i][j][status]=max(dfs(i-1,j,0,prices,dp),dfs(i-1,j-1,1,prices,dp)+prices[i]);}int maxProfit(int k,vector<int>& prices) {vector<vector<vector<int>>> dp(prices.size(),vector<vector<int>>(k+1,vector<int>(2,-1)));return dfs(prices.size()-1,k,0,prices,dp);}
};
//lambda
class Solution {
public:int maxProfit(int k,vector<int>& prices) {vector<vector<vector<int>>> dp(prices.size(),vector<vector<int>>(k+1,vector<int>(2,-1)));function<int(int,int,int)> dfs=[&](int i,int j,int status)->int{if(j<0)return INT_MIN;if(i<0)if(status==1) return INT_MIN;elsereturn 0;if(dp[i][j][status]!=-1)return dp[i][j][status];if(status==1)return dp[i][j][status]=max(dfs(i-1,j,1),dfs(i-1,j,0)-prices[i]);elsereturn dp[i][j][status]=max(dfs(i-1,j,0),dfs(i-1,j-1,1)+prices[i]);};return dfs(prices.size()-1,k,0);}
};
3.1:1翻译为动态规划
1.确定dp数组以及下标的含义

dfs换成dp就是数组以及下标含义
2.确定递推公式
dp[i+1][j][0]=max(dp[i][j][0],dp[i][j-1][1]+prices[i]);
dp[i+1][j][1]=max(dp[i][j][1],dp[i][j][0]-prices[i]);
3.dp数组如何初始化(难理解的点)
1.第一维度prices.size()+1是我们的数组下标表示天数的i从1开始
2.表示交易次数的j初始化是k+2的大小是因为
-1,0,1,2,…,k一共是k+2个状态,这一点和递归里面的对应
3.对应递归的终止条件,j必须大于0才是合法的,其他的都是不合法的,所以一开始初始化都是负无穷(除以2是为了防止溢出)
然后单独把j大于0,并且是第0天(对应i<0的if),也不持有股票(对应的是递归里的if(status==0))都赋值为0,表示这种情况下没有利润
vector<vector<vector<int>>> dp(prices.size()+1,vector<vector<int>>(k+2,vector<int>(2,INT_MIN/2)));
for(int i=1;i<=k+1;i++)dp[0][i][0]=0;
4.确定遍历顺序
后续结果需要依赖前面的计算结果,故使用从前往后遍历
for(int i=0;i<prices.size();i++){for(int j=1;j<=k+1;j++){dp[i+1][j][0]=max(dp[i][j][0],dp[i][j-1][1]+prices[i]);dp[i+1][j][1]=max(dp[i][j][1],dp[i][j][0]-prices[i]);}}
完整代码
class Solution {
public:int maxProfit(int k,vector<int>& prices) {vector<vector<vector<int>>> dp(prices.size()+1,vector<vector<int>>(k+2,vector<int>(2,INT_MIN/2)));for(int i=1;i<=k+1;i++)dp[0][i][0]=0;for(int i=0;i<prices.size();i++){for(int j=1;j<=k+1;j++){dp[i+1][j][0]=max(dp[i][j][0],dp[i][j-1][1]+prices[i]);dp[i+1][j][1]=max(dp[i][j][1],dp[i][j][0]-prices[i]);}}return dp[prices.size()][k+1][0];}
};
4.滚动数组优化
和01背包一样,前面都是i后面都是i-1
由于j要靠j-1推出来,所以需要从后往前遍历j
class Solution {
public:int maxProfit(int k,vector<int>& prices) {vector<vector<int>> dp(k+2,vector<int>(2,INT_MIN/2));for(int i=1;i<=k+1;i++)dp[i][0]=0;for(int i=0;i<prices.size();i++){for(int j=k+1;j>=1;j--){dp[j][0]=max(dp[j][0],dp[j-1][1]+prices[i]);dp[j][1]=max(dp[j][1],dp[j][0]-prices[i]);}}return dp[k+1][0];}
};
123.买卖股票的最佳时机III
[123. 买卖股票的最佳时机 III - 力扣(LeetCode)](https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii/description/)
就是上一题k=2的情况,带进去就完了,直接结束
相关文章:

Day44 | 动态规划 :状态机DP 买卖股票的最佳时机IV买卖股票的最佳时机III
Day44 | 动态规划 :状态机DP 买卖股票的最佳时机IV&&买卖股票的最佳时机III&&309.买卖股票的最佳时机含冷冻期 动态规划应该如何学习?-CSDN博客 本次题解参考自灵神的做法,大家也多多支持灵神的题解 买卖股票的最佳时机【…...
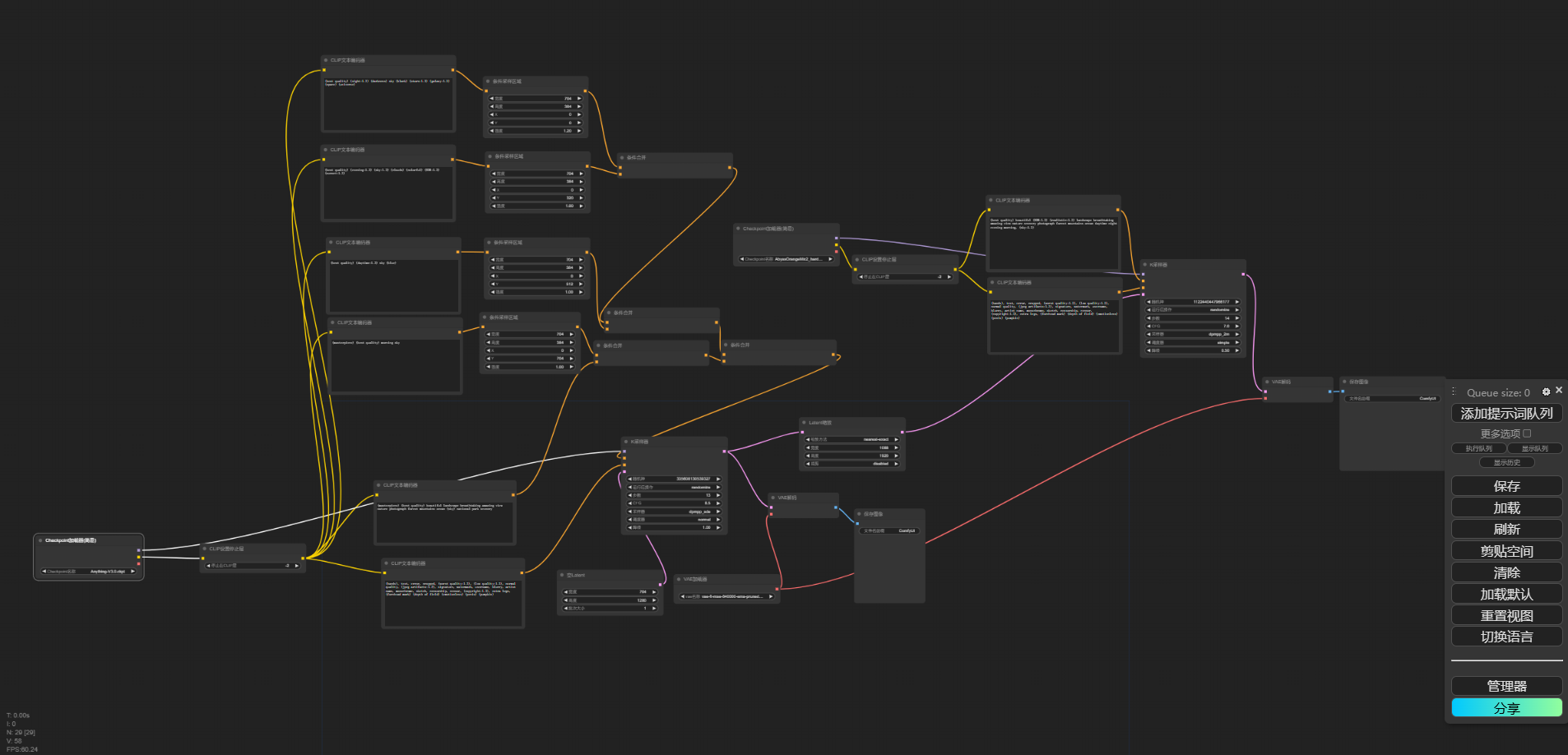
Area-Composition模型部署指南
一、介绍 本模型可以通过输入不同的提示词,然后根据各部分提示词进行融合生成图片。如下图: 此图像包含 4 个不同的区域:夜晚、傍晚、白天、早晨 二、部署 环境要求: 最低显存:10G 1. 部署ComfyUI 本篇的模型部署…...

策略模式、状态机详细解读
策略模式 (Strategy Pattern) 策略模式 (Strategy Pattern) 是一种行为型设计模式,旨在将一组算法封装成独立的类,使得它们可以相互替换。这种模式让算法的变化不会影响到使用算法的客户,减少了类之间的耦合。策略模式通常用于处理一类问题&…...

OpenWrt广播DNS到客户端
OpenWrt广播DNS到客户端 Network -> Interfaces -> lan ->DHCP Server -> Advanced Settings -> DHCP-Options 设置 6,dns1,dns2 如下图 也可以直接编辑 /etc/config/dhcp config dhcp lan list dhcp_option 6,119.29.29.29,223.5.5.5 #ipv4 option dns 2402:4…...

C++编程技巧与规范-类和对象
类和对象 1. 静态对象的探讨与全局对象的构造顺序 静态对象的探讨 类中的静态成员变量(类类型静态成员) 类中静态变量的声明与定义(类中声明类外定义) #include<iostream> using namespace std;namespace _nmspl {class A{public:A():m_i(5){…...

AutoHotKey自动热键AHK-正则表达式
在这个软件的操作中,基本都是需要即时的解决一些问题,所以对字符串的操作是比较多的,所以正则的使用还是比较重要的,接下来我们用一个例子来了解正则表达式的使用 str "7654321" RegExMatch(str, "65(43)(21)", SubPat)str ( str %str% SubPat %SubPa…...

【3D Slicer】的小白入门使用指南四
开源解剖影像浏览工具Open Anatomy Browser使用及介绍 和3D slicer米有太大关系,该工具是网页版影像数据的浏览工具(可以简单理解为网页版的3D slicer) 介绍 ● 开放解剖(OA)浏览器是由神经影像分析中心开发的,基于网络浏览器技术构建的图谱查看器。 ● OA浏览器将解剖模…...

flink同步mysql数据表到pg库
1.关闭防火墙和selinux systemctl stop firewalld systemctl disable firewalld systemctl status firewalldvi /etc/selinux/config 修改为disabled2.安装java8 yum list java-1.8* yum install java-1.8.0-openjdk* -yjava -version3.下载和部署postgresql 下载地址&#…...

AndroidStudio-常用布局
一、线性布局LinearLayout 线性布局内部的各视图有两种排列方式: 1.orientation属性值为horizontal时,内部视图在水平方向从左往右排列。 2.orientation属性值为vertical时,内部视图在垂直方向从上往下排列。 如果不指定orientation属性,…...

Vue全栈开发旅游网项目(10)-用户管理后端接口开发
1.异步用户登录\登出接口开发 1.设计公共响应数据类型 文件地址:utils/response404.py from django.http import JsonResponseclass BadRequestJsonResponse(JsonResponse):status_code 400def __init__(self, err_list, *args, **kwargs):data {"error_c…...

[Android]查找java类中声明为native方法的具体实现方法
在android代码中,经常可以看到native方法,需要查看其对应的C方法,这些方法是一一对应的,对应关系是在jni注册里关联起来的。 比较直观的是这样的例子, Parcel.java //Java层的方法里调用了native方法nativeWriteInt…...

Exploring Defeasible Reasoning in Large Language Models: A Chain-of-Thought A
文章目录 题目摘要简介准备工作数据集生成方法实验结论 题目 探索大型语言模型中的可废止推理:思路链 论文地址:http://collegepublications.co.uk/downloads/LNGAI00004.pdf#page136 摘要 许多大型语言模型 (LLM) 经过大量高质量数据语料库的训练&…...

uniapp在app模式下组件传值
在 UniApp 编译成 App 后,传递参数可以通过多种方式实现,常见的方式有以下几种: 1. 通过 URL 参数传递(适用于 WebView) 如果你的 App 页面通过 WebView 渲染,可以像在 Web 端一样通过 URL 传递参数。例如…...

Docker解决暴露2375端口引发的安全漏洞
docker的暴露api端口2375,没有任何安全防护,我们通过linux系统防火墙(iptables)来进行ip访问限制 # 查看iptables所有规则 iptables -L -nv # 只允许某个ip访问2375端口 iptables -I INPUT -s 127.0.0.1 -p tcp --dport 2375 -j A…...
HTML5+CSS前端开发【保姆级教学】+新闻文章初体验
Hello,各位编程猿们!上一篇文章介绍了前端以及软件的安装,这一篇我们要继续讲解页面更多知识点,教大家做一篇新闻题材的文章 新闻文章 当我们点开浏览器经常看到各种各样的文章,今天我们就来看看大家最喜欢关注的体育…...

『VUE』26. props实现子组件传递数据给父组件(详细图文注释)
目录 本节内容示例代码总结 欢迎关注 『VUE』 专栏,持续更新中 欢迎关注 『VUE』 专栏,持续更新中 本节内容 父组件传子组件–props 子组件传父组件–自定义事件 本节讲子组件传父组件–通过props里的方法传递,就是父亲写了一个函数,给子组件调用,然后…...

RHCE-DNS域名解析服务器
一、DNS简介 DNS ( Domain Name System )是互联网上的一项服务,它作为将域名和 IP 地址相互映射的一个分布式 数据库,能够使人更方便的访问互联网。 DNS 系统使用的是网络的查询,那么自然需要有监听的 port 。 DNS 使…...

移民统计年鉴(1996-2021年)
年鉴中包含了以下几个方面的数据: 移民数量:记录了每年全球移民的总数,以及不同国家和地区的移民流入和流出情况。 移民类型:区分了经济移民、难民、家庭团聚等不同类型的移民。 移民原因:分析了推动移民的各种因素&…...

MFC1(note)
引言 在学习SDK后我们发现,写消息好麻烦,处理消息更麻烦 处理消息效率低发送消息效率低 所以把SDK中这些消息全部封装好 MFC封装了windows 的大部分API 这里说一下QT架构跨平台 MFC用得如何取决于你SDK的水平 创建 如果打开没有MFC 一般勾选以下…...

1.1 关于游戏编程
1.1.1、游戏中客户端和服务器的交互 游戏通常采用客户端-服务器模式。在这种模式下,服务器负责处理游戏的核心逻辑、数据存储和玩家间的交互,而客户端则负责呈现游戏画面、接收玩家输入并与服务器通信。 客户端和服务器的作用和功能 客户端&a…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...
