LeetCode 热题100（八）【二叉树】（3）

目录

8.11二叉树展开为链表（中等）

8.12从前序与中序遍历序列构造二叉树（中等）

8.13路径总和III（中等）

8.14二叉树的最近公共祖先（中等）

8.15二叉树中的最大路径和（困难）

8.11二叉树展开为链表（中等）

题目描述：leetcode链接 114. 二叉树展开为链表

给你二叉树的根结点 root ，请你将它展开为一个单链表：

• 展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
• 展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1：

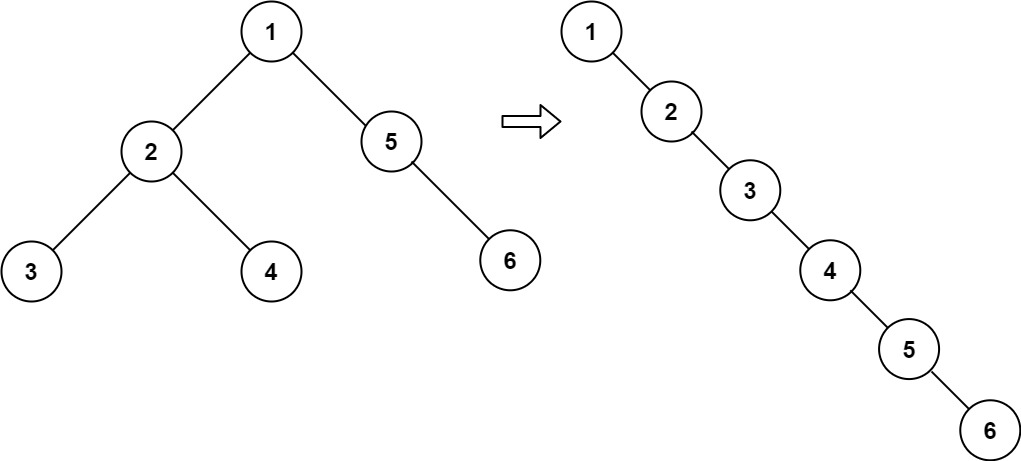
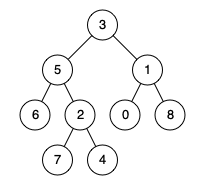
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [0]
输出：[0]

思路：

1.将左、右子树分别变为链表L和R

2.根节点的右节点变为L的根节点，根节点的左节点为空

3.L尾节点的右节点变为R的根节点

举例说明：

见上图

代码：

class Solution {
public:void flatten(TreeNode* root) {if (!root) return;flatten(root -> left);flatten(root -> right);TreeNode* temp = root -> right;root -> right = root -> left;root -> left = nullptr;while(root -> right) root = root -> right;root -> right = temp;}
};

8.12从前序与中序遍历序列构造二叉树（中等）

题目描述：leetcode链接 105. 从前序与中序遍历序列构造二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

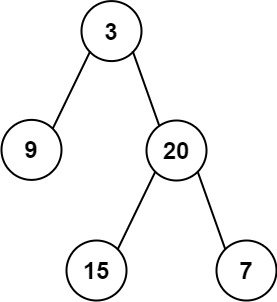
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

思路：

1.由于前序遍历的顺序是【根-左子树-右子树】，中序遍历的顺序是【左子树-根-右子树】，所以由上图的前序遍历preorder可知，它的第一个元素3为根节点。那么由中序遍历inorder可知根节点3的左侧元素为左子树，共1个元素；根节点3的右侧元素为右子树，共3个元素。

2.记录3的左子树的前序遍历顺序和中序遍历顺序，其中9即为3的左节点

记录3的右子树的前序遍历顺序和中序遍历顺序，其中20即为3的右节点

3.记录20的左子树的前序遍历顺序和中序遍历顺序，其中15即为20的左节点

记录20的右子树的前序遍历顺序和中序遍历顺序，其中7即为20的右节点

举例说明：

见上图

代码：

class Solution {
public:unordered_map<int, int> mp;TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int n = preorder.size();for (int i = 0; i < n; i++) {mp[inorder[i]] = i;}return build(preorder, inorder, 0, n - 1, 0, n - 1);}TreeNode* build(vector<int>& preorder, vector<int>& inorder, int pre_l, int pre_r, int in_l, int in_r) {if (pre_l > pre_r) return nullptr;//前序遍历中的根节点位置int pre_root = pre_l;//中序遍历中的根节点位置int in_root = mp[preorder[pre_root]];TreeNode* root = new TreeNode(preorder[pre_root]);//左子树节点个数int size_l = in_root - in_l;//构造左右子树root -> left = build(preorder, inorder, pre_root + 1, pre_root + size_l, in_l, in_root - 1);root -> right = build(preorder, inorder, pre_root + size_l + 1, pre_r, in_root + 1, in_r);return root;}
};

8.13路径总和III（中等）

题目描述：leetcode链接 437. 路径总和 III

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：

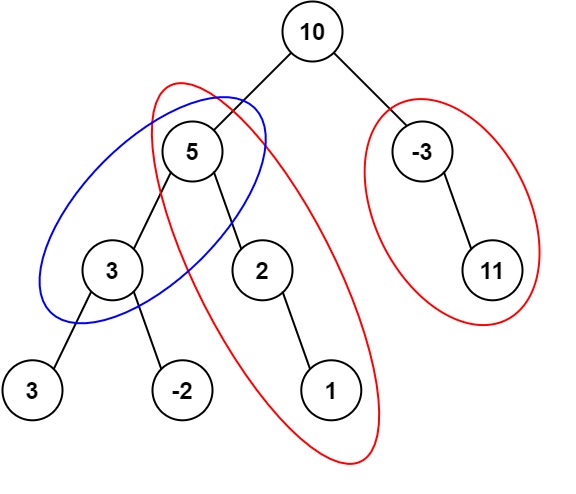
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

示例 2：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

思路：

        和560. 和为K的子数组类似，使用前缀和+哈希表的方式来解决，只不过我们现在面对的数据是存储在二叉树里面了

注：unordered_map<long, int> mp和long sum的类型为long，要不然有几个测试用例通过不了

举例说明：

无

代码：

class Solution {
public:int ans = 0;unordered_map<long, int> mp;int pathSum(TreeNode* root, int targetSum) {mp[0] = 1;dfs(root, targetSum, 0);return ans;}void dfs(TreeNode* root, int targetSum, long sum) {if (!root) return;sum += root -> val;if (mp.find(sum - targetSum) != mp.end()) ans += mp[sum - targetSum];mp[sum]++;dfs(root -> left, targetSum, sum);dfs(root -> right, targetSum, sum);mp[sum]--;}
};

8.14二叉树的最近公共祖先（中等）

题目描述：leetcode链接 236. 二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

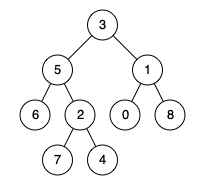
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点5和节点1的最近公共祖先是节点3

示例 2：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点5和节点4的最近公共祖先是节点5。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

思路：

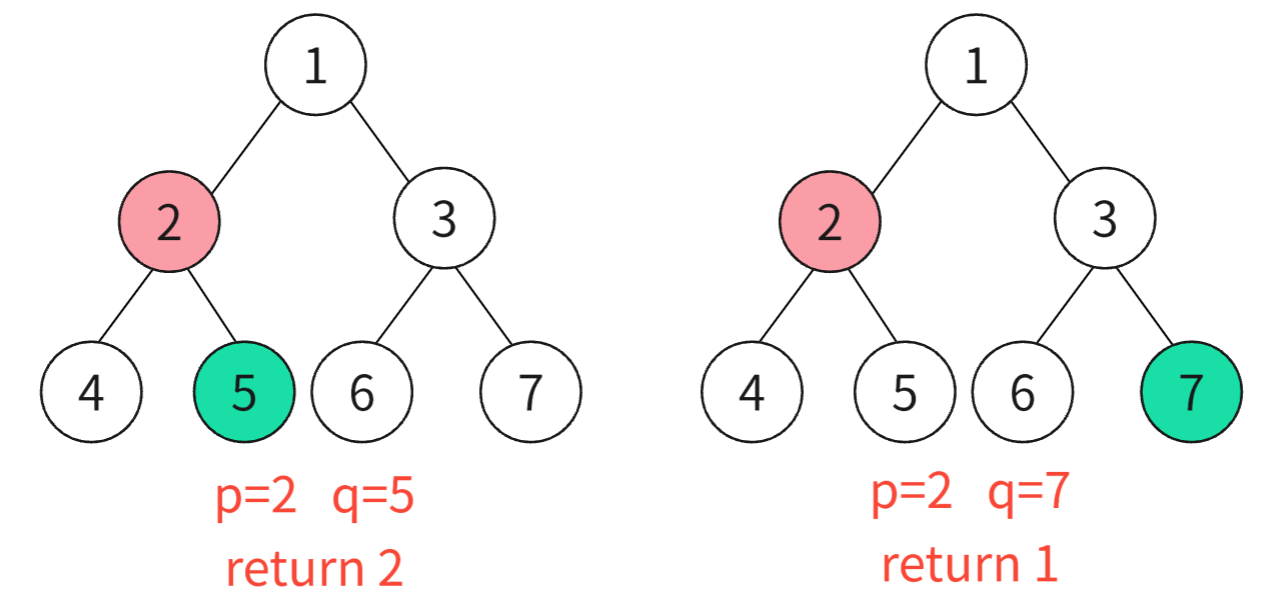
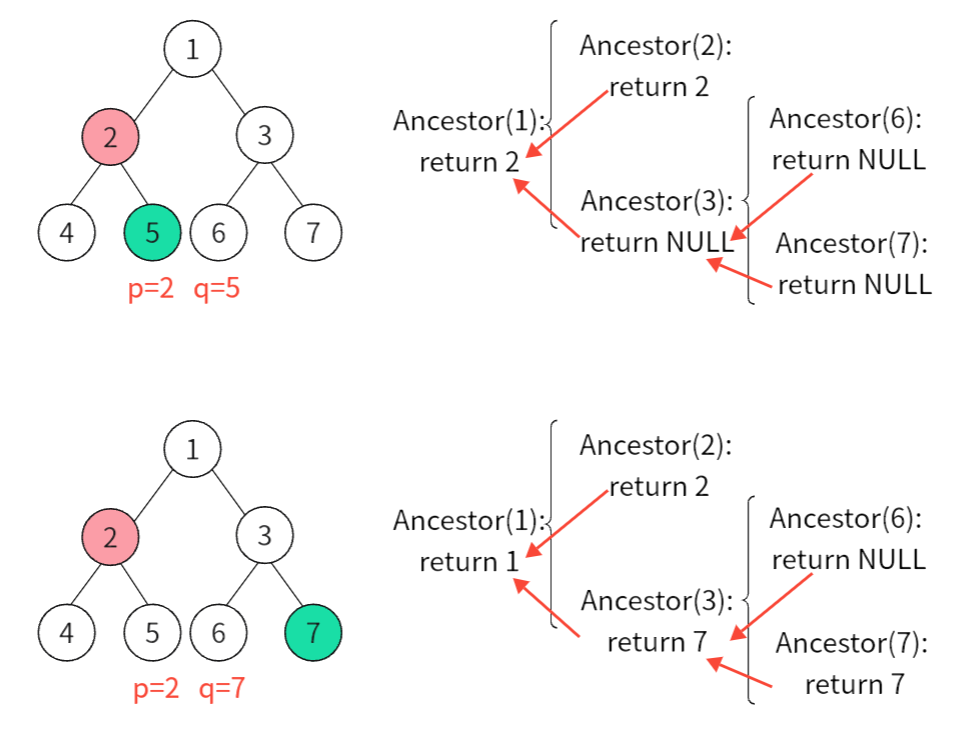
        按照p、q中一节点是否是另一节点的祖先节点可以分为上图两种情况 。

        使用递归，分以下几种情况讨论：

1.如果当前节点为空，或者等于p，或者等于q，返回当前节点

2.如果当前节点左、右子树均不返回空，返回当前节点

3.如果当前节点左子树返回不为空，右子树为空，返回左子树递归结果

4.如果当前节点右子树返回不为空，左子树为空，返回右子树递归结果

5.如果当前节点左、右子树均返回空，返回空

举例说明：

代码：

class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if (!root || root == p || root == q) {return root;}TreeNode* L = lowestCommonAncestor(root -> left, p, q);TreeNode* R = lowestCommonAncestor(root -> right, p, q);if (L && R) return root;return L ? L : R;}
};

8.15二叉树中的最大路径和（困难）

题目描述：leetcode链接 199. 二叉树中的最大路径和

二叉树中的 路径 被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

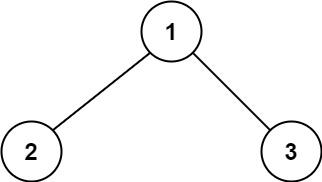
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

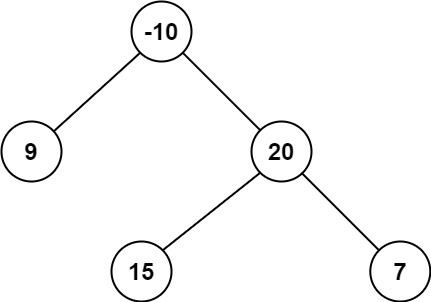
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

思路：

1.定义一个函数getNum(TreeNode* root)，可以计算root节点的贡献值

贡献值可以理解为以该节点为起点，在其子树中寻找一条路径，使其路径和最大

对空节点而言，getNum(NULL)=0

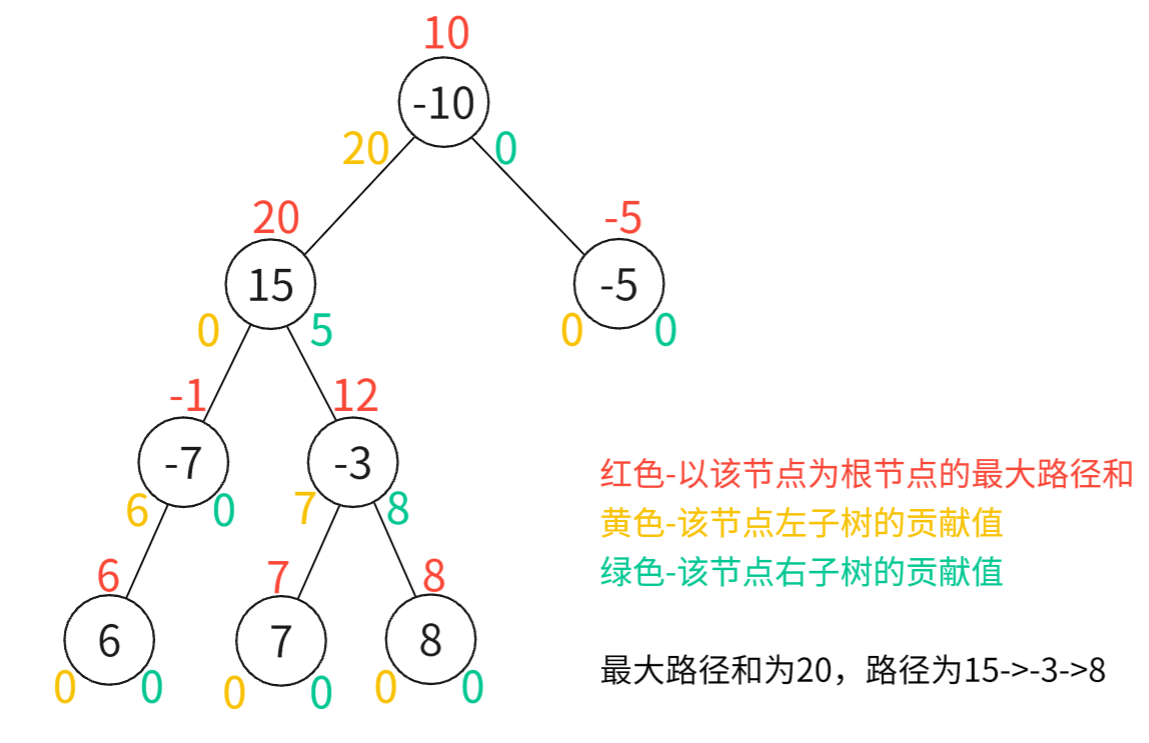
2.以下图为例，

根节点-10的路径和ans(-10)= -10+max(getNum(15), 0)+max(getNum(-5), 0)

遍历所有节点，其中ans的最大值即为二叉树的最大路径和

举例说明：

代码：

class Solution {
public:int ans = INT_MIN;int maxPathSum(TreeNode* root) {getNum(root);return ans;}int getNum(TreeNode* root){if (!root) return 0;int L = max(getNum(root -> left), 0);int R = max(getNum(root -> right), 0);ans = max(ans, root -> val + L + R);return root -> val + max(L, R);}
};